
Hello, Codeforces!
The ICPC Challenge World Finals in Luxor is approaching for some of you, and we are delighted to provide an additional exciting opportunity to compete open to all!
We are happy to invite you to the 2023 Post World Finals Online ICPC Challenge, powered by Huawei starting on May 6, 2024 at 15:00 UTC and ending on May 20, 2024 at 14:59 UTC.
In this Challenge, you will have a unique chance:
to compete with top programmers globally
to solve 1 exciting problem prepared by Huawei
to win amazing prizes from Huawei!
It is an individual competition.
2023 Post World Finals Online ICPC Challenge powered by Huawei:
Start: May 6, 2024 15:00 UTC
Finish: May 20, 2024 14:59 UTC
We hope you'll enjoy this complex Challenge!
Problem
We are glad to propose to you an exciting challenge “Accuracy-preserving summation algorithm”, which is prepared by Huawei Computing Product Line.
With this challenge, we focus on summation algorithms of floating point numbers in different precisions with the goal to use the lowest possible precision without losing too much of the accuracy of the end result. This problem arises in high-performance computing as lower precision can be computed faster. At the same time it also loses accuracy faster and can even lose it completely. Finding the right balance between fast low precision calculations and higher precision intermediate summations is a challenging task on modern architectures, and you would have an opportunity to try addressing this challenge
Prizes from Huawei
| Rank | Prize | |
| Grand Prize (Rank 1) | € 12 000 EUR + a travel trip to the 48th Annual ICPC World Finals in a guest role | |
| First Prize (Rank 2-10) | € 8,000 EUR | |
| Second Prize (Rank 11-30) | € 3,000 EUR | |
| Third Prize (Rank 31-60): | € 800 EUR | |
| TOP 200 Participants | Souvenir T-shirt | |
| * If the allocated Huawei Challenge prize cannot be delivered to your region for any reason it may be replaced by another prize (if no legal restrictions), at the discretion of the Sponsor. | ||
Challenge Rules and Conditions
By participating in this Challenge, you agree to the Challenge Rules and Conditions of Participation
Good luck, we hope this will be fun!











Why was this postponed in the first place?
I remembered about a summation problem long ago, but it got wiped out of CF and I can't find it. Now it has came back with a different name.
Is it rated?
No
I think it's rated because carrot extension column called** (just now )** is founded in standing table
Should I be registered somewhere else from CF, or CF registration for the event is sufficient to be eligible for the prizes?
According to para. 8 of the challenge rules, "only participants who entered a valid ICPC username (email address) during registration are eligible for recognition as a Challenge winner", which means (if I remember correctly) that you need your codeforces email to match your icpc.global email. It should be possible to register there even if you are not icpc-eligible (e.g. not a student).
You can probably avoid this as long as possible and only do this after the contest ends if you are among the winners, though.
so we should have an account on ICPC website?
Yes, I think so.
You can participate no matter you have an account or not. If you don't have, then you'll be invited to create one after this contest.
Best of luck for all the participant.
Hello this contest has been such a great pleasure to complete! Thank you to all the writers and editors and testers of this :) such a great contest.
How many tasks are there in this contest?
only 1
thanks
What about the T-shirts for the last challenge?
I never got mine. Did anyone?
I discovered today that it was in fact my fault. I didn't double check my address was set correctly. I just today saw that it was still pointing at my freshman dorm. The package has probably been thrown away at this point.
Thanks for the question. We realize the wait has been too long. As mentioned earlier, there were some manufacturing challenges (pardon the pun). The t-shirts, we understand, have finally arrived in EACH region globally for all the top 200 ranked contestants. Each region is now delivering the t-shirts, and we hope you will receive it soon. On behalf of Huawei, thank you for your patience!
What should I learn to reach the level that I can solve that kind of problems?
it is rated?
Have to say, I haven't spent as much money since I was born as 12000 EUR.
Can I participate in other rated contests during the two-week challenge?
When will i receive my T-shirt I got last round?
What is the perfect score?
There's a lot of minor details about the scoring process that are missing from the statement. Do you plan to release a local scorer to clarify some of them? Thank you
The testing queue is so long, i need to wait 10 minutes to get the results.
DelayForces:( I have been waiting for judging for 25 minutes, but it is still "In queue" now.
For some reason this is happening to random submissions :(
Maybe the next time we will have to write an evaluator for codeforces :)
Or write a program to predict(guess) a proper time to submit to avoid being inq
Can someone explain which order codeforces judges? I sent submission 1 hour ago. Still in queue while recent ones have been already judged.
I just noticed the grader is extremely fast, can we expect the same performace for the hidden tests?
How hard is to reach 3000points? Like how long would a code for those scores be?
Can we see other's solutions after contest is over?
Time limit is "10s", for just adding 1000000 double numbers?. I am so confused: what is the point of solving this? Spending 10s CPU time and generate a not-reusable "program" just for a specific input. Am I missing something important? Really do not understand the "real" problem behind this "abstraction".
Not only that, they don't reveal many details which are very important and you have to guess them. If you want your "real" problem solved, you don't hide any details, you provide local tester and a few tests (or test generation method).
I second this
Maybe you could think that because I'm in the lead, I've understood the task statement.
I assure you : it's not the case. I have no idea how to add two fp16 numbers in the "right" way, by which I mean the one used in the evaluator. Especially subnormal fp16.
I would like to thank the organizers for the latest announcement.
Still have no idea how they cast fp64 to fp32 or sum fp32.
Two doubles -> Two floats -> Two doubles -> Sum
Oohhh thanks a lot! And they do not cast the sum to float? Anyway I will try when I will have access to a computer
The standings changes so fast!
Organizers aren't answering questions in the contest system so I will ask here:
1) In order to compute the perfect sum $$$S_e$$$, do we read input values as fp64 (
double) or something more precise?2) What happens when we convert fp16 infinity back to fp64? Does it become infinity or e.g. the max fp16 value?
pinging @ICPCNews
1) Note that the actual binary64 value is not always exactly equal to the given decimal value. Instead, the actual given value is the closest number representable in binary64. When reading the input, most programming languages will do the conversion for you automatically.
Based on this statement, it is enough to just read input value into double without any extra actions.
2) When the algorithm performs an addition in type T, the two arguments are converted into type T, and the result is also of type T. ... The addition of two fp16 happens in fp64, but the result is immediately converted to fp16.
If I understand correctly: double a, double b -> half a, half b -> double a, double b -> double sum -> half sum
This doesn't answer my doubts :(
1) I'm asking about the definition of $$$S_e$$$, which organizers calculate "as precisely as [they] can". Is it the sum of input values, each rounded to binary64 first? Or is it the precise sum of input values, only at the end rounded to binary 64?
2) What happens when we convert fp16 infinity back to fp64?
1) I also struggle with understanding $$$S_e$$$, but if " the actual given value is the closest number representable in binary64 ", I suppose that $$$S_e$$$ is computed based on the "given values".
2) Based on my submissions, fp16 infinity converts into fp64 infinity. And it would be weird if infinity converts into some non-infinity value.
My best guess is the following: the expected sum S_e is the exact sum of input values converted to binary64. The tester has a bug, and does not calculate the sum correctly for 3 of the 76 test cases.
2) Shouldn't it be the same what happens when we convert float's infinity to double?
For 1), I have a simple algorithm that computes $$$S_e$$$. It may not give the theoretical $$$S_e$$$, but it seems to give the same $$$S_e$$$ as the evaluator. It may be that "as precisely as we can" != "as precisely as possible". I'm not sure I'm allowed to reveal more details.
I have no idea for 2).
"... I'm not sure I'm allowed to reveal more details..."
Once the contest comes to an end, feel free to reveal all the details (procedure, source code, etc.) :). I'm eager to see a good solution in action.
The fifth Huawei-CF optimization challenge was on the midway... Participants were still guessing evaluation details...
I also asked questions, but organizers aren't answering the questions...
The announcement says "When a value is fp64 or fp32, we just use the native data types." , but I don't think this is very clear. This is because IEEE 754 allows several different rounding algorithms, as explained in https://en.wikipedia.org/wiki/IEEE_754#Rounding_rules , and is dependent on languages or compilers. (Python users may be in trouble because it doesn't support fp32 calculation in build-in functions.)
It seems to be consistent with C++
doubleandfloat.In my humble opinion, these recent announcements are not entirely fair to those individuals in top positions, as they were clever enough to unravel the hidden aspects of the contest unaided. Now, they may face additional competition for the top spots. While such adjustments might be acceptable in a 'just for fun' contest, they seem unjustified here, especially considering the significant monetary stakes involved.
Fear not, top performers! I pose no threat to you! I currently reside at the bottom of the leaderboard and intend to stay there for the duration of the competition. :)
Good luck!
Come on... releasing the checker and some tests after 10 days of the competition? +Extension
I did most of the work in the first week, and planned to do very little this week. Good luck with that plan now, right?
We know that not every solution is the best solution, because there are a thousand Hamlets for a thousand readers.
The current release plan is probably the one that best meets most candidate's needs. I apologize for the impact on you.
The contest is still on, who knows what the final result will be?
Why?
"Next, we calculate the expected sum as precisely as we can"
"//'Exact' answer based on Kahan summation"
Or, the Kahan is shown but the expected sum is really exact while testing?
Hope it is.
Expected sum is not always exact. It is calculated by Kahan summation as in the published checker implementation.
My clar few days ago:
Q. In scoring, "Next, we calculate the expected sum S_e as precisely as we can" Is this mean S_e is the exact sum (after converting the inputs into binary64)?
A. The intent is that it is the closest possible binary64 value to the actual (infinite precision) sum.
... then, finding the exact sum with Kahan's algorithm is contradict with this answer, but will the checker fixed?
Is the checker numerically stable? Will it always add the same numbers to the same value?
I locally got a situation where printing extra stuff in the checker changes the sum that it computes. Maybe that's allowed in C++.
I also created a test where
s{a,b,c} != s{s{a,b},c}, but I don't understand float->double->float casting enough to say if this is incorrect.The checker seems deterministic, why would the order of operations change?
Could you share this situation or describe how to reproduce it? I don't think it should be legal in this code in standard C++, at least with IEEE 754-compliant FP arithmetic.
Could you share this test? float->double->float roundtrip should be lossless.
Edit: The example yosupo provided answers all my questions; "GNU G++17 7.3.0" doesn't strictly adhere to IEEE 754.
This code prints
1.00000000020000001655under "GNU G++17 7.3.0", and prints1.00000000000000000000under "GNU G++20 13.2". In addition to that, if we add a printf likeprintf("value: %.20lf\n", nums.top()); currResultSingle += static_cast<float>(nums.top());, the result changes to1.00000000000000000000under "GNU G++17 7.3.0".Interesting. I was aware of this issue a while ago, but lately couldn't reproduce it so discarded the knowledge as no longer relevant in practice. Thank you!
It looks like the checker behavior is as follows:
For
dsums, the accumulator containing the running binary64 sum and the next binary64 number to sum are expanded to 80-bit (long double) floating-point numbers, added, and then rounded back to binary64.For
ssums, the binary64 numbers to sum are rounded to binary32 and then expanded to 80 bits and added into an 80-bit accumulator, except that whenever there are a multiple of 64 numbers left to add, counting the number just added, the accumulator is rounded to binary32 and then expanded back to 80 bits. The accumulator is rounded to binary64 to give the final value of the sum.For
hsums, the accumulator is a 16-bit floating-point number, according to the nonstandard format explained in the contest announcements. Each addend is truncated to the 16-bit format; then the accumulator and addend are expanded to 80 bits, added, rounded to binary64, and then truncated back to 16 bits.This strange behavior, including the behavior changing when you insert prints, is similar to other excess precision problems in C++, as mentioned in this blog post; it happens when the compiler produces code that uses the 80-bit 8087 registers. This problem generally doesn't occur when compiling for the 64-bit architecture as compilers use the SSE2 instructions instead.
terminelo profe
¡Dale, un esfuercito más y llegamos al top 20! ¡Vamos, vamos! :)
reduce the submission rate limits NOW or i riot
Is it the reason you are so rude? Who is afraid of you??
Will the tests really be completely different in the end or will some new tests get added?
I try to use Python Decimal library to calculate the more accurate results, but that seems different with the results calculated in checker. And Kahan will also lose precision during summation. Can I assume that we are not expected to calculate the most accurate answer, but the answer that matches the checker most?
For example, this self defined input: 5 -1.577492e-05 -2.576098e-05 3.994e-3 100000 -99999.3233. If we load them as double in python and sum through decimal, the result is 0.6806524640963445590490334732164390274533616321. But through checker the result is 0.68065246409969404339790344238281. There are several bits difference, which will lead to a big score downgrade in accuracy.
Yes you can assume they use Kahan algorithm to compute Se and not the exact sum.
Thanks for confirming. It really takes me some time to realize this and I am struggling to match checker's behavior.
Queue is stuck. Both new solutions and the ones with ongoing testing aren't progressing at the moment
You are right, but we can't get verdicts as fast as before now.
So, can codeforces allocate only 10% to other submissions?
In this contest, you can never assume that you have achieved an absolute lead.
Dear problem managers, I would really appreciate if you would put some submission restriction.
It won't change much at this point anyway. The queue is almost 1 hour, and the contest ends in 2 hours anyway.
Quick unrelated question. Your profile says you're working at Huawei, doesn't that prevent you from participating ?
I use it in CF as my affiliation but I'm not an employee (and I don't have access to codebase). I sometimes help with events (B2B), e.g. I did workshops for their interns last year, a Summer online IOI camp, a China trip for ICPC students soon.
Btw. I hope they will let me organize future CF Challenges. There were a lot of issues with this one.
the standing is on fire
Let’s send our North Korean homie Sung.An to world finals.
When can we see others solution?
Yes! Please, please, please! Now, as everyone reading this post envisions me holding a hat and begging for a tip, what a grotesque image of myself! Hahaha :).
Never. Every porblem that huawei have a practical application in theirs proprietary researches. So they wont make it opensource
Thank you.
Here is a graph showing ranking on the leaderboard vs. score, and how it changed between May 12 and just before the end of the contest, on May 23.
Here is an enlargement of the upper left corner.
Here are the preliminary scores (x axis) shown against the final scores (y axis):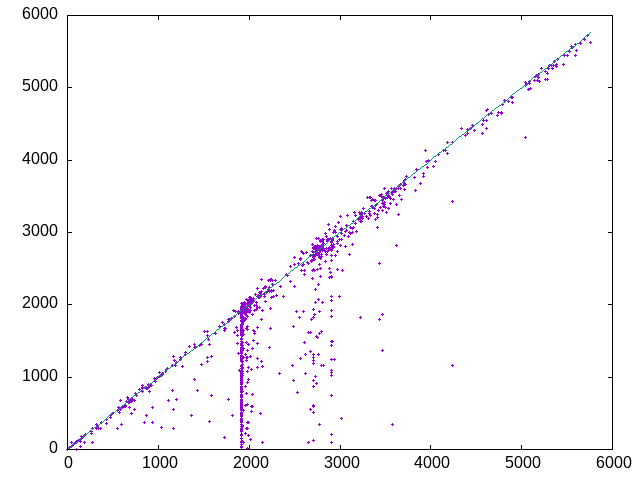
I have provisional 6th place. My main idea for 5000+ points:
Build a binary tree, make sure to keep every block of 16 elements as one subtree. Greedily assign the fastest possible operation in every node (Half, Single, Double). Never decrease the type from child to parent. In random order, iterate leaves and greedily upgrade the operation type if it decreases the total error (this requires updating the path to the root, like in a segment tree). Now use meet in the middle: for each child of the root, consider $$$K \approx 10^5$$$ possibilities of what few changes we should make to slightly modify the result. Sort the possible results in two children of the root, use two pointers to find the best pair. Like in birthday paradox, this is actually like considering $$$K^2$$$ possibilities.
Improvements:
I'm very afraid that the final tests will be so different that my algorithm (2) will be useless.
And I have no idea how the top 1-2 achieved their scores.
As I understand, the dfs-order of leaves in your solution is always 0, 1, 2, etc? In other words, do you even change their order? If no, then what is the point of "make sure to keep every block of 16 elements as one subtree"?
That's a reasonable question. The point (3) describes some examples of changing order. Though 5000+ points is possible with just 0..n-1 order.
Some other small improvement: if I'm extremely close to the final sum, I collect nodes close to the root, shuffle them, rebuild that part of the tree, calculate the new sum and see if it's better. This approach shifts around bigger blocks, e.g. sizes 1024. And I try random orders for small $$$N$$$, basically ignoring the order penalty.
By the way, if you split everything into blocks of size 16 and then shuffle them, then you will probably have about $$$(16-k)n/32$$$ cache misses, where $$$k$$$ is the size of the last block.
Yup. I always use the uneven block last. I came up with a nice hack: don't worry about it in the solution, but (when printing the tree) first go to child with size divisible by 16.
Thank you very much for sharing your approach, and congratulations on a top result!
Can you also share the scores you got on individual tests?
For three of the tests (#72-74) the value of $$$S_e$$$ used by the checker was wrong, meaning that it wasn't the value of the infinitely precise sum rounded to the nearest binary64 number. Did this make any difference? I had to special-case these tests.
I think that I didn't do anything particular for those tests. Once the checker was published, I just copied their kahan sum to compute the target sum. I don't remember if my scores improved thanks to that.
If you dont mind, can you please share your code for the final submission?
If it's allowed, I will share my code.
Hi! First of all I would like to congratulate you for the amazing score and performance you achieved at this contest! Now, I want to say I saw a very interesting thing at your submissions when I was looking at the top scores submissions, I saw that you had a lot of them that achieved 1920 points, which is the same as a simple solution of liniarly itereting on the numbers. Could you please tell me what was the idea or problem behind this score ?
Data mining. I used asserts and memory allocation to get some information about tests. You can read about it in the past Huawei Challenges.
Is there any sense to get information about the tests. if our solution will be judged in the final tests
Can you also describe how did you pick which operation use for a Node (Half, Single or Double)? I see that you wrote "Greedily assign the fastest possible operation", but I couldn't come up with any greedy that will improve my score (instead of decreasing score).
And I am very surprised that 5000+ points can be obtained by only using the following order: 0, 1, 2, ..., n — 1
First I greedily assign the fastest operation that doesn't compute infinity. So:
This obviously creates a big final error and a terrible score, much worse than using only DOUBLE operations. In my previous comment (starting from "In random order"), I explained how I upgrade those operations (HALF->SINGLE and SINGLE->DOUBLE) to decrease the error, eventually getting it down to 0, usually.
Think about this easier problem: Given a sequence of random values in range 1..1e9, insert operators
+and-between them to get a sum equal to 0. Solution: insert operators at random first, then flip some of them to slightly improve the total sum, then use MITM to consider a lot of possible sets of changes at the same time, hopefully getting the sum 0.Note that it's the order of leaves. We build a (balanced) binary tree.
Okay, I got it. Initially, I didn't get an idea of updating the path to the root. Yes, I agree, I did the same (constructed a binary tree), but you already said the best score for me was when all my operations were DOUBLE.
Thank you so much for the explanation and congrats :)
If you don't mind, can you please explain your approach?
My solution is based on maintaining a list of numbers, with the invariant that their exact sum is the target sum. The goal is then to reduce this list to a single element. The transitions are:
The main subroutine takes a list of pairs (precise value, approximate value), and produces a list with as many approximate values as possible. For each input pair, the error is the difference between the two values.
At the end of this process, we have written the total error as the sum of lots of small positive errors. Each of these small errors corresponds to a sublist of the input list of pairs. For each such sublist, we check whether replacing all precise values by the corresponding approximate values preserves the target sum.
This subroutine is used in various places, most importantly to create blocks of 16 numbers. Each block is initialized with the fp64 sum of the 16 numbers. (With some randomization of the permutation of the 16 numbers, it is possible to reach the target sum). We want to instead compute each block using fp16 and/or fp32 operations. We can compute some candidate tree for each block; such a tree determines an approximate value for the block. The above subroutine will try to use as many of these approximate values as possible.
I didn't achieve good scores, but look at the spreadsheet I used to analyze my solutions! (this was the first time I used such simple technique as "visualize my results")
I want to share the testcase data I extracted using memory allocation I learnt from last ICPC challenge. It shows some distribution or feature of each testcase. The value is not accurate since I use square root or log10 for those large values, but you can know the rough magnitude. Here ld is long double, d is double, s is single, h is half. Also log is the log10 and error is the accuracy error calculated from score.
Are the standings final? I don’t believe the final tests have been run, but the scoreboard says final standings.
The standings are not final. The final solutions will be run against a hidden set of testcases.
There is a bug in
mingw-w64implementation ofscanf, which is used by the checker (Codeforces testing system is run on Windows). If you're using any method of input other thanscanfand it's relatives, you'll sometimes get different last bit when reading numbers compared to what the checker sees. This results in a difference in the final sum between you and the checker if this bit is high enough. In this problem 1 bit of difference means you'll get half the points for the test. The probability of the bug is1/4096for numbers that are not representable exactly bylong double(most decimals, e.g.0.1,0.12,0.123,..). In my tests the probability was around1/4300. I found this bug, because my sum and checker's sum were different in last bit on some of my random tests.P.S. Apparently the bug only works if the number is written with less than 17 digits of precision. Otherwise we get 0 in first extra
long doublemantissa bit and everything is A-OK. So the bug is absent in all numbers from tests#16and#10, because they have 19 digits of precision. But if there are long tests like#5(with 7 digits of precision), there will be problemsP.P.S. Don't blame me for not telling everyone during contest. I wasn't aware of it until the last day.
Example: godbolt
If you're using
mingw-w64(like Codeforces does), this will give you⛔.1337.1337221in binary looks like this10100111001.0010001000111011100111001000111001000000101000000000001101000...In
long doubleit gets rounded to 64 bits of precision10100111001.00100010001110111001110010001110010000001010000000000In
doubleit gets rounded to 53 bits of precision10100111001.001000100011101110011100100011100100000011But if we round from
long doubletodouble(ties to even, which is the default rounding mode), we get10100111001.001000100011101110011100100011100100000010Another example is
1337.133767110100111001.0010001000111110100011111000011111000111110111111111111000000...10100111001.0010001000111110100011111000011111000111111000000000010100111001.001000100011111010001111100001111100011111Rounding from
long doubletodouble(ties to even) gives10100111001.001000100011111010001111100001111100100000godbolt
__mingw_strtoldis used instead of just__mingw_strtodatmingw-w64/11.0.1/mingw-w64-crt/stdio/mingw_vfscanf.c:1345
__mingw_sformat (_IFP *s, const char *format, va_list argp)1345
d = (double) __mingw_strtold (wbuf, &tmp_wbuf_ptr/*, flags & USE_GROUP*/);__mingw_vsscanf (const char *s, const char *format, va_list argp)1630
return __mingw_sformat (&ifp, format, argp);293
int sscanf(const char *__source, const char *__format, ...)297
__retval = __mingw_vsscanf( __source, __format, __local_argv );173
#include <cstdio>static inline double stringToDouble(InStream &in, const char *buffer) {3562
int scanned = std::sscanf(buffer, "%lf%s", &result, suffix);double InStream::readReal() {3904
return stringToDouble(*this, readWord());double InStream::readReal(double minv, double maxv, const std::string &variableName) {3912
double result = readReal();double InStream::readDouble(double minv, double maxv, const std::string &variableName) {3952
return readReal(minv, maxv, variableName);12
#include "testlib.h"363
vec[i] = inf.readDouble(-1.7976931348623157e+308, 1.7976931348623157e+308, format("value number %d from sequence",i+1).c_str());Fun fact: there is no bug if you
#include <stdio.h>instead of<cstdio>, but only if there are no other C++ headers included before it. The solution to this mystery lies in the depths oflibstdc++config/os/mingw32-w64/os_defines.h:l51Update:
The bug is absent in preliminary tests
Reported to mingw-w64/bugs/989
Reported to testlib/issues/203
I used some very funny ideas:
Suppose we want to compute the exact sum $$$S_e$$$ with a mantissa of 52 bits. Then I first search for two input values $$$x$$$ and $$$y$$$ such that summing them in double precision gives a number with a mantissa that has the same bits as the 29 last bits of $$$S_e$$$. As in most cases $$$N^2 » 2^{29}$$$, $$$x$$$ and $$$y$$$ can be easily found in $$$\mathcal{O}(N \log N)$$$.
Now I can build a tree with the $$$N-2$$$ remaining values. My only condition for building this tree is $$$\texttt{float(T) + (x+y)} = S_e$$$, such that I just have to compute the sum of the remaining values with a precision of 23 bits instead of 52 bits. That way it's easier to use float summations.
But we can also repeat this process if $$$T$$$ can be cast to fp16. It's possible to search for two input values $$$z$$$ and $$$w$$$ such that $$$z+w$$$ has the same bits as the last $$$13$$$ bits of $$$float(T)$$$. That way I can compute a tree $$$T'$$$ with the $$$N-4$$$ remaining values such that $$$\texttt{float(fp16(T') + (z+w))} = \texttt{float(T)}$$$ That way I can compute $$$T'$$$ with a 10 bits precision and make it easier to use fp16 summation.
In the end my tree looks like $$$\verb|{d: {s: {d: {h:T'}, {d: z, w}}}, {d: x, y}}|$$$
Very interesting idea! Could you share your results on the tests because I'm curious how your solution did, especially when it didn't find a sum of 2 numbers with the required last bits. Or did you have some improvements to handle this case?
For the last 29 bits, I always found a correct pair except for cases in 72-78 range and 1-12 range (and 43 if I'm not wrong). For the last 13 bits of $$$\texttt{float(T)}$$$ I only search when $$$T$$$ can be cast in fp16 and I always succeed except for cases 32, 37, 39 and 40 for which I have no clue why I did not find :(
Thanks! I think the tests 72-78 were specifically created in a way to counter a lot of solutions. You can even see that by the n given in those tests(n=100, 1000, 100000 while on the others n is more random). For the tests 1-12 and 43 n is small(<=10000) so perhaps your solution didn't have a big enough sample of numbers to find the numbers. Weird for the fp16 cases but maybe it's related to the way approximation works in fp16 like in the example Errichto gave: −60000+0.01≈−59970. So it really seems like overall the solution consistently finds a pair which is very satisfying haha
Lol, this is so clever and funny at the same time.
There was no need for custom janky fp16. Both Intel and AMD have F16C extension since SSE2 times (2011-2012), it's supported by GCC 12+ and Clang 15+ as
_Float16and since C++23 asstd::float16_t.For small test, I ran some simple SA where I randomly move nodes around (keeping block of 16) and changing the type. For most tests, I am trying something a bit smarter:
I needed a special case for the least significant bit where I need one of the two values to not be rounded up.
To build the tree:
This work well for most seed from 11 to 71 (one exception at 42 I think) and 75/76, and for the other my SA works decently.
One issue here is that cast 16 only goes down (in absolute value) so when the input is all positive, we can't really use them unless we start with number that are close to a float16 to start with. The max score will usually be 63 there. For most other cases it's possible to achieve 81.
Nice solution!
Checker issues aside, it's great that there was such a variety of ideas.
Thanks.
The contest was very poorly designed, I can't imagine that's what they were expecting to get, but that aside, the problem was actually interesting with many ideas that could achieve a good result. Of course I am also biased by the final result, had I not performed well, I would just remember the headache to get it working and not the interesting ideas that came along the way =)
Thanks for sharing your methods! I have some problem understanding your method in “ pick two values such as the error of the cast has its most significant bit matching”. What is the error here means? Value in fp64 minus value in fp32? And what is the most significant bit here means, is that in the exponent of the error? I just want to understand the brief idea behind this method. Thanks!
Yes correct, the error is val — fp32(val) or val — fp16(val). And the most significant bit is the exponent, because I can basically flip that bit by casting or not casting. If I can do that for all the bits, then I can fix the final errors.
my best submission scored 5k+ points, but the last one was 4k+, can I contact someone to solve this problem?(
Is it still possible to register on the ICPC website? I don't know where to find the competition there.
When will the system test be conducted?
P/s: Nice contest, and there are quite a lot of simple but efficient solutions in the comments which really amaze me :).
I want the system to be able to test both the last commit and the highest scoring commit, so that people like me who scored low on the last commit will not lose the score they deserve.
I think that the reason it is not done this way is because it favours randomised solutions. However, I think it would be great to have an opportunity to know whether the solution failed one of the main tests due to RE/TL/ML, as done in some other competitions.
I tried to write to the organizers to test my best submission, as the latter has a very poor score, but they do not respond(
I think it can be unfair to tell the organizers to use one particular solution because now that the participants can communicate with each other and test the system outside the contest time, you could illegitimately know which solution is better.
Also, would you take the max of those scores? Then people who sent their best scoring code last would be at a disadvantage since the system would test only one solution.
I agree with you in some ways, but I wrote about the situation to the organizers almost immediately after the end of the competition until I could test anything after the end of the competition, also I could not resubmit my best submission because of the 10 minutes limit, besides I am not asking to choose a certain submission, but to choose the one that is the best and is displayed in the table right now. I spent quite a lot of effort and time on the competition(
I don't understand why I got a negative vote, I just wanted to make my point clear, obviously I knew it couldn't be and I should pay for my mistakes
Because people(including me),thinks your point is totally wrong.
It seems that the final judging is over and the tests are very similar. I guess that organizers used the same generator method, just with different seeds. Here are some statistics, assuming that nothing will change.
maxplus didn't lose many points and thus climbed to the first place, congrats. The top10 didn't change but the threshold dropped around 60-70 points. Three new people got into top30, and obviously three people dropped down.
How to view the final rankings?
When I execute my code on my self-generated random test with N = 10^6 and each number has the form A.BCDEFGHIJKLMNOPQRSTeX where -300 <= X <= 300, it takes over 9 seconds to finish (and I got more than 47.14 points which indicates perfect accuracy). However the same code run for less than 5 seconds on each test of the organizer. Does that mean the final system tests are still weak somehow?
Most of the system test have a low X since you can't really cast big numbers to fp16 or fp32 without getting +-INF. You could indeed try to sum some of them until they get low enough to cast them, but the odds of it actually happening in the test are so low there was almost no profit in doing so.
Aside from that, reading the numbers as string and parsing them to long doubles was the only way i found to get the same Kahan sum as the checker did.
Is there going to be any plagiarism tests before the prizes are distributed or should I lose hope as I placed 205 ;(
Hi, everyone! I've finished 9th this time. And this was by a margin the hardest contest for me so far.
I had a kind of unique approach from the start and faith in it until the very end. But I was struggling so hard to guess the correct way of calculating fp16 addition, so basically I started to optimize something only on 11th day, after the checker's code was published :)
Let me share the idea with you. First of all, I split the input array into two parts.
First part consists of 90-97.5% of elements. The main goal is to get the minimum W as possible, keeping an absolute error relatively low
Second part is the "compensator". Let's build a balanced tree. Leafs are elements, internal nodes are operations. All the internal operations are fp64, and only the lowest level of operations (between two leaves) might be fp32 or fp16. We can approximate desired error almost transparently by choosing between different type of operation on the lowest level (other operations on the path to the root of the tree are fp64, so we usually don't lose any precision there)
The main challenge is how to keep the absolute error in the first part relatively low. You can notice that rounding during fp16 addition always truncate the result towards zero. It's not a problem if array is balanced in terms of the number of positive and negative elemtents. So actually the main problem is how to use as much fp16 operations as possible if array is not balanced at all
Without loss of generality, let's consider that the array consists only of positive number.
Consider following approach:
Split the array to some number of blocks of predetermined size (let's say blockSize = 16 to get rid of random memory access penalty)
Sum up all the elements in each block constructing a balanced tree using as much fp16/fp32 operations as possible. We almost don't care about resulting error right there
Sum up all the blocks one by one choosing between fp32 and fp64. We should pick fp32 only if rounding helps to lower the error. The "compensated" amount of each step is the rounding error, which clearly depends on magnitude of addendums. But this is a good news since all the elements are positive, partial sum will increase after each step, so we would compensate bigger amount closer to the end of blocks summation process
This approach allows us to get a relatively low resulting error (which most probably might be compensated by the second part) even if all the elements have the same sign. In worst case scenario we have to skip some worst (in terms of increasing error) fp16 operations during blocks sum calculation
1: Полное решение [7624 ms, 0 MB, 0 points]
2: Полное решение [8296 ms, 0 MB, 0 points]
3: Полное решение [8186 ms, 0 MB, 47.14 points]
4: Полное решение [7218 ms, 0 MB, 47.14 points]
5: Полное решение [8046 ms, 0 MB, 47.14 points]
6: Полное решение [7046 ms, 0 MB, 47.14 points]
7: Полное решение [7874 ms, 0 MB, 47.14 points]
8: Полное решение [15 ms, 0 MB, 81.65 points]
9: Полное решение [46 ms, 0 MB, 81.649 points]
10: Полное решение [8234 ms, 0 MB, 47.14 points]
11: Полное решение [8078 ms, 0 MB, 57.321 points]
12: Полное решение [7671 ms, 0 MB, 62.885 points]
13: Полное решение [8296 ms, 29 MB, 62.92 points]
14: Полное решение [7983 ms, 92 MB, 62.669 points]
15: Полное решение [7937 ms, 145 MB, 62.466 points]
16: Полное решение [8124 ms, 35 MB, 74.987 points]
17: Полное решение [8139 ms, 89 MB, 74.946 points]
18: Полное решение [6999 ms, 142 MB, 74.458 points]
19: Полное решение [6656 ms, 37 MB, 79.457 points]
20: Полное решение [8405 ms, 89 MB, 79.504 points]
21: Полное решение [7796 ms, 144 MB, 78.857 points]
22: Полное решение [8078 ms, 32 MB, 78.587 points]
23: Полное решение [8546 ms, 90 MB, 79.703 points]
24: Полное решение [7999 ms, 136 MB, 79.05 points]
25: Полное решение [7999 ms, 34 MB, 79.34 points]
26: Полное решение [8265 ms, 97 MB, 79.721 points]
27: Полное решение [8217 ms, 145 MB, 79.306 points]
28: Полное решение [7734 ms, 34 MB, 79.475 points]
29: Полное решение [8421 ms, 90 MB, 79.722 points]
30: Полное решение [8437 ms, 137 MB, 79.705 points]
31: Полное решение [8078 ms, 28 MB, 79.638 points]
32: Полное решение [8311 ms, 33 MB, 79.505 points]
33: Полное решение [6328 ms, 94 MB, 77.537 points]
34: Полное решение [8171 ms, 149 MB, 76.142 points]
35: Полное решение [8155 ms, 37 MB, 79.491 points]
36: Полное решение [8140 ms, 95 MB, 79.627 points]
37: Полное решение [8640 ms, 146 MB, 76.843 points]
38: Полное решение [7703 ms, 40 MB, 79.603 points]
39: Полное решение [8250 ms, 94 MB, 79.115 points]
40: Полное решение [8655 ms, 144 MB, 79.37 points]
41: Полное решение [7889 ms, 33 MB, 79.268 points]
42: Полное решение [7046 ms, 33 MB, 80.002 points]
43: Полное решение [46 ms, 0 MB, 57.671 points]
44: Полное решение [7686 ms, 92 MB, 79.672 points]
45: Полное решение [8327 ms, 144 MB, 78.958 points]
46: Полное решение [6764 ms, 34 MB, 79.959 points]
47: Полное решение [8468 ms, 92 MB, 79.912 points]
48: Полное решение [7968 ms, 150 MB, 78.949 points]
49: Полное решение [7921 ms, 42 MB, 80.008 points]
50: Полное решение [8234 ms, 90 MB, 79.748 points]
51: Полное решение [8421 ms, 148 MB, 79.036 points]
52: Полное решение [5468 ms, 34 MB, 73.418 points]
53: Полное решение [6984 ms, 93 MB, 79.454 points]
54: Полное решение [6984 ms, 150 MB, 60.974 points]
55: Полное решение [8375 ms, 39 MB, 79.398 points]
56: Полное решение [8249 ms, 95 MB, 71.3 points]
57: Полное решение [8483 ms, 145 MB, 78.671 points]
58: Полное решение [7421 ms, 39 MB, 69.153 points]
59: Полное решение [8421 ms, 93 MB, 69.203 points]
60: Полное решение [7734 ms, 147 MB, 78.999 points]
61: Полное решение [7640 ms, 32 MB, 79.898 points]
62: Полное решение [8327 ms, 34 MB, 78.269 points]
63: Полное решение [8077 ms, 92 MB, 77.874 points]
64: Полное решение [7640 ms, 142 MB, 77.357 points]
65: Полное решение [7155 ms, 34 MB, 78.605 points]
66: Полное решение [7046 ms, 91 MB, 77.851 points]
67: Полное решение [8468 ms, 145 MB, 77.338 points]
68: Полное решение [7780 ms, 39 MB, 78.466 points]
69: Полное решение [7109 ms, 90 MB, 77.872 points]
70: Полное решение [5733 ms, 140 MB, 73.484 points]
71: Полное решение [7467 ms, 36 MB, 78.257 points]
72: Полное решение [15 ms, 0 MB, 66.188 points]
73: Полное решение [577 ms, 13 MB, 47.476 points]
74: Полное решение [46 ms, 0 MB, 65.8 points]
75: Полное решение [6327 ms, 0 MB, 73.815 points]
76: Полное решение [8374 ms, 13 MB, 73.356 points]
77: Полное решение [31 ms, 0 MB, 53.292 points]
78: Полное решение [593 ms, 14 MB, 41.996 points]
thank you for sharing
the ones who does not have positive contribution can not make a comment with image ****
thank you
Just so you just realize how useless and impractical this task is:
If you round numbers in fp16 you never reduce the error => using replacing fp64 with fp16 you only increase the answer.
Is it logical that fp32 should also not reduce the answer? Yes.... but a bunch of bugs in the author checker changes the problem dramatically.
As it should be: We use fp64 to somehow reduce the answer, then use fp16, fp32 to increase it. And the task is to gnaw the scores, because it is really hard to do it (even ~55 on a random test). Butooooooooooooooooooooooooooo, we have a different task. We have fp64, which can calculate the answer very slightly inaccurately. We have fp16, which only increases. And there's fp32, which doesn't know how to behave at all.
And as if a task in which we would have to think about rounding and how it works is even slightly meaningful. But a task where we???????? where we can make random changes in the response thanks to incorrect authoring code is a task that can never be applied anywhere.
If you pay attention to the changes brought by GPU chips, you may guess the original purpose of this topic. Unfortunately, some hardware conditions cannot be fully simulated. Therefore, some adjustments and changes have been made to the question. Thank you very much for your suggestions, We will continue to optimize and improve. Congratulations on entering the TOP60 list.
I was expecting a problem to minimize the error, but it turned out to be a problem to cancel the error knowing the accurate answer. Still a fun problem, but it seems not as useful in practice as advertised (they said "addressing this challenge", not "a problem inspired by this challenge"). It would be surprising to me if the organizer could use any of the algorithms in this contest on their chips.
In the last ICPC Challenge between 2023/11-12, there was a message about prize from System (via user talks) roughly 2 days after the contest ends. However, this time no message was confirmed yet. I'm really worrying about the possibility that I missed something, but are there some participants who already received some message?
I haven't received any messages yet.
Thank you for sharing information.
+1
Same here.
Hello E869120!
The top 200 ranked participants in the Challenge were contacted two weeks ago by Codeforces, with a form for information.
The data of that form was submitted to Huawei and Prize distribution and Contact to all Cash prize winners will begin this week.
I hope that helps.
Hello Codeforces! Thank you all for participating in the Post WF ICPC Challenge powered by Huawei! The final standing ranks were submitted, and those that placed in the top 200 received a form to fill out for distribution of the Cash prizes and t-shirts.
That data collected was provided to Huawei on Monday of this week — and those that filled out the form will be receiving their participation t-shirts in the next two months. Distribution to the various countries will begin by the end of this week — and then forwarded to you via the individual country distribution point.
Cash prize winners will be contacted directly by Huawei to obtain additional banking information for the distribution of the prize money.
Thanks again for participating! Stay tuned for exciting ICPC Challenge powered by Huawei updates!
Hello Codeforces who placed in the top 200! Is there anybody who received Huawei prize? Not only have I not received my prize money yet, but I haven't even received any notification from Huwai about it. Thanks.
Hello there, Final standings for the Post World finals ICPC Challenge can be found here: https://mirror.codeforces.com/contest/1953/standings
The prizes for the top 200 — t-shirts — as mentioned above, Huawei have begun distribution to the individual countries; the cash prize winners have been contacted by Huawei directly, and are underway.
Hope that helps.
I have not been contacted about the cash prize. Should I just wait, or?
thanks Maxplus We were made aware by Huawei that that all had been contacted. Let me follow up with them immediately.
With my personal problem, I was not able to contact with Huawei but now they are not response. How can I receive payment as of now? Is not possible?
Did anyone receive their prize t-shirts? It's been more than two months, and I haven't even received any emails. Since I provided my contact information in the form, I was under the assumption that we would be notified or updated about the status of our prize. However, I have received nothing via email, phone, or WhatsApp.
I didn't receive the T-shirt either. :(
It seems like Huawei doesn’t really care about the prize distribution for this contest. It’s a shame that the people in the top spots haven’t even been contacted about their prize money, let alone about our t-shirts.
I've received the prize money but am still waiting for 2 T-shirts.
Yea, I guessed that most people would receive their prize money; otherwise, there would've been a backlash regarding such an amount of monetary prizes not being awarded lol. However, based on a couple of comments, it seems like the prize distribution has been rather sloppy or poorly executed.