ap_hawkdown's blog

Sieve of Eratosthenes
By ap_hawkdown, 10 years ago, In English

Sieve of Eratosthenes used to determine prime numbers. A bool array in taken and initialized to false
first of all it starts with 2 and updates index of bool array of all multiples of 2 to be true..

like 4,6,8..but not 2 which is kept false. next false number is picked which is 3..and all its multiples are updated true like 6,9,12,15...updated true but 3 is kept false

similarly it is followed..

all numbers in the end which are false are primes.

then next false number is picked

int main() { static bool b[100000];

for(int i=2;i<=30000;i+=1)

{

if(!b[i])

{for(int j=2;j*i<30000;j++)

{

    b[i*j]=true;

}

}

} for(int i=2;i<30000;i++)

{

if(!b[i])

{

printf("%d",i);

}

}

return 0;

}

  • Vote: I like it
  • -11
  • Vote: I do not like it

»
10 years ago, # |
  Vote: I like it -7 Vote: I do not like it

We can reduce the number of iterations.

We only need to iterate i from 2 to sqrt(N), where N is the upper bound.

And j can start from i.

Check this code.

This is because any composite number has a divisor that does not exceed its square root.

(proof: Let n be a composite. There exists a, b (1 < a <= b < n) s.t. a*b=n. Then a must be less than or equal to sqrt(n))

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Actually it's not the asymptotic optimization.

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it -8 Vote: I do not like it

      What is asymptotic optimization?

      → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Sieve of Eratosthenes works in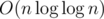 your optimization don't make it better.

        → Reply
        • »
          »
          »
          »
          »
          10 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          I just said we can reduce the number of iterations. I didn't say I optimized it nor my code has better time complexity.

          → Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it

    Your code is not really most optimized. See my code: http://pastebin.com/fi2f9HCN

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Could you tell me which part is different?

      → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
          Vote: I like it +4 Vote: I do not like it

        I used j+=i instead of j++ in for (int j=i*i; j<N; j+=i) And because global array is initialized by zero, I named my array NonPrime instead of IsPrime to avoid for (int i = 1; i <= N; i++) is_prime[i]=1;.

        P/S: I got TLE in one problem use this sieve. By a trade-off between readablity and performance. My following code run faster 3x.


        NonPrime[0]=NonPrime[1]=true;

for (int i=2; i<=3; i++) 
for (int j=i*i; j<N; j+=i) 
NonPrime[j]=true;

for (int i=5, k=4; i*i<N; i+=(k^=6)) 
if (!NonPrime[i]) 
for (int j=i*i; j<N; j+=i) 
NonPrime[j]=true;

        First loop means we remove numbers 6k, 6k+2, 6k+3, 6k+4. Second loop means we try to iterate 5, 7, 11, 13, 17, 19, ... (6k-1 and 6k+1)

        → Reply
»
10 years ago, # |
← Rev. 2   Vote: I like it +8 Vote: I do not like it

If you just want to generate prime number in [1,n], you can try this simple algorithm. It's running time is O(n).

→ Reply
»
10 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

your suggestions are welcomed. Guys i am just beginner programmer.This is my very first post.It may not be best solution but i posted it for beginner programmers(easy to understand) and my future reference.

Thanks for your suggestions in the matter.

→ Reply