DIV2A-DZY Loves Chessboard
Just output the chessboard like this:
WBWBWBWB...
BWBWBWBW...
WBWBWBWB...
...
Don't forget to left '-' as it is. The time complexity is O(nm).
check the C++ code here.
DIV2B-DZY Loves Chemistry
It's easy to find that answer is equal to 2n - v, where v is the number of connected components.
check the C++ code here.
DIV1A-DZY Loves Physics
If there is a connected induced subgraph containing more than 2 nodes with the maximum density. The density of every connected induced subgraph of it that contains only one edge can be represented as 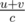 , where u, v are the values of the two nodes linked by the edge. The density of the bigger connected induced subgraph is at most
, where u, v are the values of the two nodes linked by the edge. The density of the bigger connected induced subgraph is at most 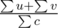 .
.
If 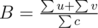 , and for every edge,
, and for every edge, 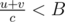 . Then we'll have u + v < Bc, and
. Then we'll have u + v < Bc, and 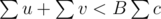 , and
, and 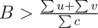 , it leads to contradiction.
, it leads to contradiction.
So just check every single node, and every 2 nodes linked by an edge.
The time complexity is O(n + m).
check the C++ code here.
DIV1B-DZY Loves FFT
Firstly, you should notice that A, B are given randomly.
Then there're many ways to solve this problem, I just introduce one of them.
This algorithm can get Ci one by one. Firstly, choose an s. Then check if Ci equals to n, n - 1, n - 2... n - s + 1. If none of is the answer, just calculate Ci by brute force.
The excepted time complexity to calculate Ci - 1 is around
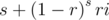
where 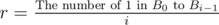 .
.
Just choose an s to make the formula as small as possible. The worst excepted number of operations is around tens of million.
check the C++ code here.
DIV1C-DZY Loves Colors
The only thing you need to notice is that if there are many continuous units with the same uppermost color, just merge them in one big unit. Every time painting continuous units, such big units will only increase by at most 3. Then you can use STL set to solve it. But anyway, a segment tree is useful enough, check the C++ solution here.
The time complexity is  .
.
DIV1D-DZY Loves Strings
We can solve a subproblem in which all the query strings are characters only first. The problem becomes calculating the shortest substring containing two given characters.
If character ch appears more than T times in S, use brute force with time complexity O(|S|) to calculate all the queries containing ch. Obviously, there are at most O(|S| / T) such ch in S.
Otherwise, we consider two sorted sequences, just merge them with time complexity O(T)(Both of the two characters appear at most T times). Being merging, you can get the answer.
So the complexity is O(TQ + |S|2 / T). We can choose 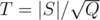 , then the complexity is
, then the complexity is 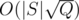 .
.
And short substring is almost the same with characters.
Check the C++ code here.
DIV1E-DZY Loves Planting
Firstly, use binary search. We need to determine whether the answer can be bigger than L. Then, every pair (i, Pi) must contain at least one edge which length is bigger than L. It's a problem like bipartite graph matching, and we can use maxflow algorithm to solve it.
We create 2 nodes for every node i of the original tree. We call one of the nodes Li, and the other Ri. And we need a source s and a terminal t. Link s to every Li with upper bound 1, and link Ri to t with upper bound xi. Then if the path between node a and node b contains an edge with value larger than L, link La and Rb with upper bound 1. This means they can match. Every time we build such graph, we must check O(N2) pairs of nodes, so number of edges of the network is O(N2).
We can make it better. Consider the process of \texttt{Divide and Conquer} of a tree, This algorithm can either based on node or edge. And The one based on edge is simpler in this problem. Now, there are two subtrees Tx, Ty on two sides, we record the maximum edge from every node i to the current edge we split, we call it MAXLi.
Suppose Lx is in Tx and Ry is in Ty (it is almost the same in contrast). We create two new nodes Gx, Gy in the network to represent the two subtrees. Add edges (Li, Gx, ∞) (i is in Tx) and edges (Gy, Ri, ∞) (i is in Ty). If i is in Tx and MAXLi > L, we add an edge (Li, Gy, ∞). If j is in Ty and MAXLj > L, we add an edge (Gx, Rj, ∞).
Then use maxflow algorithm. The number of nodes in the network is O(N) and the number of edges in the network is  . So the total complexity is
. So the total complexity is 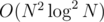 with really small constant.
with really small constant.
Check the C++ code here.
This is what I supposed DIV1-E will be. And thank subscriber for coming up with a really good algorithm with time complexity O(nα(n)) 7025382. And maybe others have the same idea. This is my mistake, and I feel sorry for not noticing that, I'm too naive, and not good at solving problems. Please forgive me.










It's easy to find that...
When I clicked to 7032804. I got this message "You are not allowed to view the requested page". Help me please.
I would be thankful if you could put a sample accepted code for each problem so that we could understand your explanation better. It's easy to put a sample code for your explanations.
The editorial is very unclear in almost all problems. Lots of steps are being skipped.
Can somebody please explain why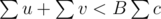 leads to a contradiction?
leads to a contradiction?
Because it leads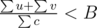
What does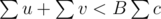 denote? How is
denote? How is
udifferent fromvin this context? (Problem B)values of u and v can be added many times, but inclusive they'll lower than B*sum(c)
Why is the answer to B. 2^(n-v)?
Think greedy. We want to maximize number of time we multiply danger by 2, so if we first put chemical number i, after that, we should put chemical number j with j-i can react, and so on, ... => One of optimal order is DFS order of graph — build from the input. So, just generate vertices in DFS order and caculate the result.
Now, "It's easy to find that answer is equal to 2n - v, where v is the number of connected components."
Sorry for my English.
I don't understand this santence :
"And every time when DZY pours a chemical, if there are already one or more chemicals in the test tube that can react with it, the danger of the test tube will be multiplied by 2."
For example, if 1 reacts with 2; 3 reacts with 4;, as for me it does not matter in which order they will be, let 3rd and 1st chemicals are in a tude, then we add 2nd and increases danger(because there is 1st chemical in a tude), then similarly add 4th and increases danger.
Sorry for my English.
There are cases when the order matters.
Think of the test case where you have 3 chemicals. 1 reacts with 3, 2 reacts with 3.
Putting 1, 2, 3 in the order only gives 2 danger, but putting 3 first gives 4 danger.
OMG... I tried to calculate the MIN danger, which should be 2^(n — v) where v is the vertices number of the max complete sub-graph, which is NP... it bordered me so long since I find that it's just a misunderstanding when reading this....
If you create a graph (vertices are the chemicals, edge from x to y exists only when x reacts with y), you will get some connected components. So, if the component's vertices are x1, x2, x3, you may put x1 first, x2 second etc. The answer is multiplies by 2^(comp size — 1). That's why, answer is 2^(n — number of components)
Sorry for my stupid question, but is the graph directed ?
Edit: Yes, the graph is directed. I foolishly assumed that if chemical x reacts with chemical y, then y should react with x too.
No the graph is undirected.
Lol,
that's why
May be you meant, undirected?
Thanks for your comment. And, sorry for my foolishness.
Suppose the number of nodes in a connected component C is x, then except the first node, all other nodes of that component will react doubling the danger every time. So for one connected component the danger will be 2^(x-1). Similarly for each connected component the danger will be 2^((# nodes in that component)-1). And the final result will be multiplication of all these results which is 2^(n-v) where v is the number of connected components.
Hope it clears your doubt.
I can't understand Div1 B,please someone help me:
what is S,we need to choose S randomly?
it s hard contest
and hard editorial ))
It's easy to find...I don't think it is easy. I think about it for 4-5 min. but i couldn't find 'why'?
Do you think 4-5 min is much? :P
I didn't say much. But if it's easy,-I think- it have to be finds under 5 minutes :/
Can someone explain with more detail Div 1 C Loves Colors problem?
yes please
Here we go :)
We maintain two structures:
When dealing with the first operation i.e. update on interval [p,q] with color c, take all intervals which are covered by [p,q] and for each of them we know that the colorfulness of all units within this interval will increase by a constant = abs(c — color_of_covered_interval), therefore we update the second structure accordingly.
For the second operation just take a sum of colorfulness from a given range.
Some more details on those structures:
We store those intervals sorted by their beginning in, for example, a set. It is straightforward how to find all intervals covered by given [p,q]. We can also notice that the total number of intervals covered by some other will be linear in terms of the number of update operations (exercise: why?), so we can simply iterate over them. When inserting a new interval, delete all those which are covered and split those which are covered partially.
This structure can be implemented as a counting tree, where in each node we store two things: sum of all updates on this node (U) and sum of its children's values (C). To update an interval by value V, go down the tree and add V to respective nodes (precisely, to their U values), not forgetting to update their C on a way back. To take a sum of an interval, again go down the tree and sum up all U values multiplied by the number of elements in a node's subtree.
If you have any questions or found any mistakes, let me know. I hope I helped
thnx alot for your explanation but i have a question why should we make the segment tree for colours not for segments i mean if we want to update a segment which contains different colours why is this wrong ? for example if we have a segment which its colours are 1,2,3,4 and we want to update [1,3] if we have the sum of [1,3] then we can increase the value by abs(sum-new value*3) ?
I'm not sure if I understood you right, but I'll try to address your doubts.
Of course you can update a segment containing different colors, the question is how; note that when updating an uniform interval you know the value to update with (as I wrote in my post). In other case the value is different for different units within the interval and I don't know how it is possible to update it.
it wrongs with me in test case 6 and i am trying to understand but i think that in the example i told u if i update for ex [1,3] and change it twice then it is only possible to know the answer of [1,3] but if i want to query on [1,1] it will output wrong answer right ?
Why taking all intervals covered doesn't lead to a quadratic complexity? — "When dealing with the first operation i.e. update on interval [p,q] with color c, take all intervals which are covered by [p,q]"
On each update every interval we iterate through we unite in one big interval. Then in the worst case we split the leftmost and the rightmost intervals, which leads to 2 extra intervals per one query. With the total of m queries and n intervals in the beginning this leads to no more than n + 2m iterations in total.
Yup, thanks!
I still dont get the n+2m argument. I get that in the worst case we create 2 extra intervals per query but what is n+2m? I solved the problem assuming it doesnt get TLE. can someone please elaborate on estimating the time complexity of the solution? EDIT: I believe it has something to do with amortized complexity. Each query appears to have O(N) complexity however intuitively I feel amortized complexity must be better but i cant prove it yet. :/
Let's say that every time we iterate over an interval completely, we destroy it. Also, every for every query, we are creating a new range to contain this new range. Now we can see that in every query, we iterate over some ranges completely and 2 ranges partially(at max).
Now let's have a look at the complexity...
We have n intervals to begin with. The total number of ranges that are created are m(one for every query).
The total number of sets that we iterate are either the partial ones, 2 per query (2m) or the ones that are created and destroyed. The ones that are created and destroyed cannot exceed (n+m) as that is the max which can be created.
Hence the total number of sets that we can ever iterate upon is (2m+ n + m). Which is amortized O(1).
Hope it helps.
It seems that DIv1-B can be solved in O(n) even if the sequence is not random
How? Can you write the rough idea?
Firstly, sort a in decreasing order and maintain the indexes in the original sequence. Let's assume that ap1 ≥ ap2 ≥ ... ≥ apn. Next, for each i (1 ≤ i ≤ n), find the smallest j (i < j ≤ n) where bj = 1 and let it zj.
To know the value of c1..n, we can apply this simple algorithm:
This is too slow to get accepted. The only thing left to make this algorithm faster is to skip js where 'c[j+k-1] == 0'. Let gi the smallest j where i ≤ j ≤ n and cj = 0. If we maintain g in every moment, the algorithm will be efficient. Fortunately, we can use disjoint-set data structure to do this. If any
c[t]becomes non-zero, we can update g by applying some operations such asg[t] = get_root_of_group(t+1).If we implement the
get_root_of_groupfunction using path-compression, the time complexity of this algorithm is O(n × α(n)).If every element in array b equals zero,then we can not skip any c[i].I think, in this case, your algorithm will TLE.
Nope. In that case, even the simple solution will work because it skips all j where bj = 0.
you are right :)
Its overall time complexity is O(NlogN) cuz it has the sorting step. That's a quite good solution though.
this is permutation,so you can sort in O(n)
Although there are so many positive votes, I have a doubt about the time complexity of the solution. We can jump to the position independently where
b[j] == 1using z, andc[j+k-1] == 0using g. But we cannot jump to the position where bothb[j] == 1andc[j+k-1] == 0in one jump. If we jump using array g, the value of j changes andb[j] == 1is not guaranteed on that point. Hence, we may jump multiple times to reach target point, which obviously takes more than O(α(N)). Therefore, I think O(N × α(N)) is not correct time complexity.I've seen your submission(7031026), and your code also jumps multiple times inside loop.(comment was added by me)
Can someone please explain Div1-A. It's not clear in the editorial how the equation leads to contradiction.
We known that for each edge we have Wu + Wv < Bc. Let's sum this over all edges from a component. We get that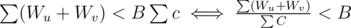 . On the other hand, the numerator of the less side is not less than numerator of the right side (because it just sums some vertices twice and more), and denominators are equal. Contradiction.
. On the other hand, the numerator of the less side is not less than numerator of the right side (because it just sums some vertices twice and more), and denominators are equal. Contradiction.
I couldn't get why order of chemicals is important in Div. 2 Problem B. And, I don't understand the contradiction in Div. 2 Problem C. Please help.
Well, the order of chemicals in problem B undoubtedly is very important. For instance, if you consider the answer "1 3 2" for the third sample, you will make sure that it's truth.
What the hell is S in FFT Problem??
S = 1e3
42
Div 1 C tutorial is very unclear for me anyone can explain what should i do in detail ?
Is the code for Div1 C really the correct? http://ideone.com/vZrnSF For me that seems like Div1B code.
Respect to editorial :P
Mail/PM the editorialist if you want to (learnt from past experience :p)
Sorry. Fixed
That will be great to include comments in judge's code.
In the div2 c problem why the third graph is not an induced graph, It satisfies all the property of the induced sub graph??
The third graph doesn't satisfy all properties of an induced subgraph. By the definition of induced subgraph, if there exists an edge from u to v and both u and v are in the subgraph, that edge has to be a part of the subgraph.
What was the significance of the number 27777500 in Div1B ?
(27777500 * 37 + 10007) mod 1000000007 = 27777500 :D
...which means that the permutations used when shuffling a and b will behave as sufficiently random ones
Test cases for DIV1 D are very weak. My solution 7030220 works in O(n) per query (always using 2 pointers/merging idea) and it passed. I've already created test that gives
in custom test.
upd. improved it to Invocation failed [TIME_LIMIT_EXCEEDED]
It can be proved intuitively that your program (hash & memorize queries) can work out the result in 1s. To hack the program, I suppose that the string consists with k repeating parts, each of which has a length of |S|/k. With memorized queries, your program will spend O(k) time on calculating only when there’s a new query. And the number of different queries is at most min{4*(|S|/k)*(|S|/k),Q}.
Let's discuss the value range of k.
Thus, min{4*(|S|/k)*(|S|/k),Q}*k is always under 1e8.
Your program will never TLE :)
Sorry, for me it is hard to understand your proof, and it might turn out that I totally misunderstood you... But I think you are wrong. Structure of testcase that you described is far from worst one.
Lets take a look at string aaaaaaaaaaaaaaaaaaa.....aaaaaaiqtgalgasuoasdklqt...iiowerioqtwyblghbzclg.
Suppose it has 35000 a at the beginning and 15000 of some random stuff after that.
First of all, how much different substrings of size 1..4 are there in second part? I am a bit tired now and too lazy to analyze hypothetical worst case, so i just ran this code few times:
And it shows that usually we will have 25000+ different substrings.
For every unique substring X we may construct 4 different queries:
a Xaa Xaaa Xaaaa XNow we have 100k+ unique queries)
How much time it takes to solve one query? We are talking about O(K) solution... And K will be ~35000 for every query (all entrances of a/aa/aaa/aaaa string + 1 or few entrances of X).
It gives us 35000*100000=3.5e9 operations. It does not looks so good as your 1e8) Also my implementation is really messy))
You may try it by yourself, it is easy to add some random build-in generator to my code in following way:
and run it in custom test — it works ~9.5 seconds even on such random testcase.
Did anyone who solved div1 A followed a more intuitive line of thought? I understand the proof by contradiction, but I can't see myself doing it during a contest (one would have to "guess" that the optimal way of choosing was choosing a single edge, and then, if needed, you'd prove it with the proof given in editorial). I'm more interested in how people developed this solution during contest.
Guessing is a good technique...
I assumed that there has to be some short greedy solution. If the subgraph would contain more than 2 nodes, the code would already become complex, so I assumed that it's enough to select 2 nodes (n = 500 also indicates that the solution should be O(n^2)). Then I tried to construct a counterexample where this doesn't work and didn't find any, so I decided to code the solution. Then I was happy to see that it passed all the pretests.
but the actual solution is only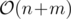 .
. 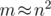 , so the solution is effectively
, so the solution is effectively 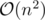 .
.
PS: ofcourse, in the worst case, we will have
Usually I think this question too. But for this contest I did't need it.
I wrote lots of code. http://mirror.codeforces.com/contest/445/submission/7030714
But it didn't work. So i printed answer step by step. Then i saw, answer of first step is equal to answer of tests, for sample tests. Then I thought adding more edges and nodes, makes answer smaller. I tried it on a paper and prove it.
Sorry for my poor English...
here's the proof.
say we have an edge of weight connecting nodes with values
connecting nodes with values  and
and  and another edge of weight
and another edge of weight 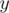 connecting nodes with values
connecting nodes with values  and
and  .
.
this is a contradiction because problem statement says that all node values and edge weights are positive. so our assumption was wrong, i.e. single edge is always the right answer.
Same with my proof...
Nice proof. the contradiction is much clearer this way.
After you cross multiply and get cx > ay + by and ay > bx + cx you can replace ay in the first inequation with bx + cx from the second one and you get cx > bx + cx + by a.k.a. bx + by < 0.
I got the idea from your proof, but it seems to me replacing stuff is more intuitive than adding stuff out of nowhere.
yes, that was what i initially did on the paper when i proved it.
but u can't always replace stuff in inequations. i have once failed a Div-1 500 because i made this mistake (replacing both ≥ with > makes it AC), so i didn't take any chances this time.
I like to make my own small cases and solve them. If you have solved 4 or 5 of your own, it's very likely that you'll realize that the solution is always a single edge.
It's also helpful to check standings. You can see there are a lot of Div 1 contestants who solved it within 10 min. That means that the coding should be very simple.
thanks for the replies pllk,kalimm and HidenoriS. I have a hard time on creating test cases and checking for a pattern on other problems than mathematical ones.
DIV2B-DZY Loves Chemistry
I found all of contestants solve it using DFS or UFDS(union find disjoint set)
am I the only one to solve it greedy ?
Can you explain how ? (I didn't solve it at all so I want to try to code all the solutions).
Why so many downvotes ? Did I say something wrong ?
Used greedy here as well. The first chemical is the one with most "connections" (number of chemicals it reacts with). After that, I just check all unused chemicals if they can make a reaction, and if there are more than 2, I just take the one with the biggest number of connections again.
Much easier solution of A div1.
I used DP on graph approarch O(n^2) or O(n^3) time and O(n^2) memory ( I can't prove both time difficulties. I am very bad at mathematichs. I fail mathematics problems at contests very often):
Lets think. First: every node of graph we my use in our answer or not. For one node answer=0. For each connected component of the graph we calculate dp indepentently and try to improve answer. For each new connected component we start our dynamics. We have array dp[i] — the best way to choose i connected nodes from graph, also we have to memyrize the set of nodes wich gives us best result. Boarder case is when we choose 2 nodes. For each new connected component we start our dfs. For each node we try to use it with other conneted node in pair and try to improve dp[2] if dp[2] is improved we should update set whitch gives us this result ( to nodes which form this pair ). We don't know how to calculate dp[i], i > 2. Don't worry. Just run on array dp[i], i from n-1 to 2 and try to improve dp[i+1]. We have a set whith shows us best result for fixed size. So try to use it. If our node is connected with one or more nodes from our set we can use this node to improve dp[i+1]. Just check dp[i+1] with result of set for i with our node. For this we should keep for each set also sum weight of edges and sum weight of nodes in two different arrays. If dp[i+1] is improved we should update value of dp[i+1], update our set and don't forget to update our two arrays with sum weight of edges and nodes. For each connected component we should destroy old array "dp" and other arrays ( it's not nessasary if you have good implementation skills ). After each connected component we should improve answer by dp[i], 2<=i<=n.
Here is my solution for better understanding:7030646
Thank you, this is the easiest solution for this problem i've ever seen :)
I don't really see the easy way to prove the fact that the best answer for i + 1 has the best answer for i as it's subset.
Edit: counterexample: graph with successively connected vertices 5-6-1-3-6-4, numbers are weights of vertices. Weights of edges are all 1. The best answer for 2 vertices is 5-6, the best answer for 3 vertices is 3-6-4.
So your algo only works because the answer is always in dp[2] :P
OMG. The solution in editorial easier in many many times. You right. I was not sure in my solution.It's a pitty for me that i can't understend the proof about dp[2] :<
Hi xyz111, thanks very much for these cool problems! I am a little confused about the solution of DIV1D. Since number of a single character (or short string) could be as many as |S|/T such that its frequency is larger than T, it is possible that the number of a pair of character/short string could be as many as (|S|/T)^2, such that at least one of their frequencies is larger than T. In this case, the time complexity would be:
O( T*Q + (|S|/T)^2 * |S|)
and of course, here we can still use the balancing idea, but the T will be |S|/(Q^1/3), then time complexity is: O(|S|*Q^2/3) Am I wrong at some point?
I'm the author of Div1D. If one of the pairs of query characters appears more than T times in S(we consider the bigger one is A),then use O(N) bruteforce.And note if we do this all the query contain A can be done.
We do the O(T) merge only if both of the two characters appear at most T times in S. So the complexity is correct.
Can someone explaine the idea of DIV1 E by using dsu? Now I have get it.
can you explain it to me?
I will write this only for unleashing my anger, and not for personal issues against this particular authors and/or round. No need to reply. The editorials of Codeforces SUCK!!! Why do they suck? Because:
they are usually fulfilled of "it's easy to find that ..." (from now on, let's call it ETF). Who cares about the ease to find something? It's a tutorial on how to solve the problem dude; it should mention AT LEAST some hint on how to solve it. Writing ETF doesn't helps, and moreover kills the inspiration to solve the problem.
in the particular case of (some) Russian authors, the use of Google Translate transforms the tutorial text into a comedy or into some misleading and confusing text (or both). Not good.
eventually, this factors cause that the solutions to the problems are mostly discussed in the forums and the messages in the editorial blog. So, the editorial blog only purpose is to gather comments about the round problems? If so, rename "editorial" to "discussion" at least, to avoid the shame.
not always the editorial are supported by source code implementing the approach described by author, which in turn, given the above arguments makes it suck infinitely more.
Ergo, the editorials really suck, and I don't see that the Codeforces fellows care about it, since it has been like that for a while. I love Codeforces; take this as a constructive critic. Suggestions would be great. Good luck!
some people solved div1 C using segement tree like this 7040202 , could someone explain that solution?
the idea for segment tree solution is to deal with every range which contains the same colour as 1 unit and of course i mean consecutive range and u will have 2 arrays 1 for current colour and the other for the sum of colourfulness and you will use lazy propagation here is my submission i hope it can make things clearer for u :) http://mirror.codeforces.com/contest/445/submission/7035631
No, your solution is different from this 7040202 solution.
You can try to solve this problem with your method.
Could someone explain more bout solution using fenwick tree on Div1 C ? Or, specifically, how can we maintain range of color if we dont use segtree? Thanks
very nice set or problems
Can someone link me to a solution for Div 2. B (DZY Loves Chemistry) that uses Disjoint-Set Datastructures?
I don't get how the STL solution works for Div1 C.
To delete a subsequence, it seems we need to know the 'width' of each element, but STL doesn't have a way to provide that..
Could someone help me figure out what "delta", "sum" and "mark" mean in the example solution for "DIV1C-DZY Loves Colors"? Thanks.
That's look like "lazy propagation of colorness", "sum of colorness", and "same color of range"
In your proposed solution to Div1-E, how do you get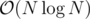 edges? If you divide and conquer on tree edges, you cannot ensure that both subtree sizes are at most some constant fraction of the total tree size. An example tree would be the one where the node 1 is connected to every other node. One of the resulting subtrees will have size N - 1, and you recurse into that. So you will have
edges? If you divide and conquer on tree edges, you cannot ensure that both subtree sizes are at most some constant fraction of the total tree size. An example tree would be the one where the node 1 is connected to every other node. One of the resulting subtrees will have size N - 1, and you recurse into that. So you will have 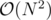 edges in total, and I feel like you are only saved by the fact that your maxflow implementation solves this particular case fast enough. Am I missing something?
edges in total, and I feel like you are only saved by the fact that your maxflow implementation solves this particular case fast enough. Am I missing something?
Can someone please explain me the solution given in the editorial for Div 1 problem C.DZY loves colors? What are the 3 arrays for?
My solution for Div1D differs from the editorial one and it's complexity $$$\mathcal{O}(N \sqrt{Q} \log{N} + Q \log{Q})$$$ is worse too. But it uses the optimization used in DSU-on-tree technique, which I've never used before outside of DSU-on-tree. I'm guessing this kind of optimizations have a general name that I'm unaware of? Kindly let me know if there is such a name. Since this solution hasn't been discussed above, I'd like to share it (Also I'll be glad if someone could verify if my complexity calculation is correct).
For a string $$$sa$$$ of length at most $$$4$$$, let's hash it with a $$$4$$$-digit number $$$a$$$. Simply, replace every character of $$$sa$$$ with the order of the corresponding digit and if $$$|sa| < 4$$$, then pad with $$$0$$$'s to fill up the rest of the digits. For example, $$$\text{hash}(aba) = 0121$$$. Now, notice that there are in total $$$27^4$$$ such hashes.
For all possible hash $$$a$$$ with corresponding string $$$sa$$$, precalculate the vector $$$pos[a]$$$ which stores the indexes of occurrences of $$$sa$$$ in the original string $$$s$$$ in sorted order.
Now, suppose that we need to solve the query $$$(sa, sb)$$$ with corresponding hashes $$$(a, b)$$$. First check if we've already solved this pair earlier, if so we're done, otherwise let's find it. WLOG assume that $$$|pos[a]| \le |pos[b]|$$$, this is important. Then iterate over $$$pos[a]$$$ to fix the position $$$i$$$ of $$$sa$$$ in the original string, then using binary search on $$$pos[b]$$$ find the closest occurrences of $$$sb$$$ in the original string after $$$i$$$ and before $$$i$$$. Update the answer using these two values.
After solving this query, store the answer in some convenient data structure (for example,
map<pair<int, int>, int>in C++) to use it for later queries if needed.I have a rough sketch of proof that the total cost of iterations over $$$pos[a]$$$ over all queries don't exceed $$$\mathcal{O}(N \sqrt{Q})$$$. And because of the binary search per iteration and
maplookup per query, overall complexity is $$$\mathcal{O}(N \sqrt{Q} \log{N} + Q \log{Q})$$$.Here's the proof:
Suppose the hashes are,
such that,
Then, for a query $$$(sa, sb)$$$ with hashes $$$(a, b)$$$, the larger $$$\min(|pos[a]|, |pos[b]|)$$$ is the more costly the iteration is going to be. So, by greedily picking the queries, worst case scenario is,
So, the worst case total iterations is,
Notice that, since $$$|pos[a_{k - (l - 1)}]|$$$ holds the maximum weight, we should maximize it to $$$\frac{N}{l}$$$. Continuing with this reasoning, we find that in the worst case $$$|pos[a_k]| = |pos[a_{k - 1}]| = \cdots = |pos[a_{k - (l - 1)}]| = \frac{N}{l}$$$.
So,
Link to my submission.