I came across an equation, but I am not able to prove it. Can somebody help me proving this equation.
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3985 |
| 2 | jiangly | 3814 |
| 3 | jqdai0815 | 3682 |
| 4 | Benq | 3529 |
| 5 | orzdevinwang | 3526 |
| 6 | ksun48 | 3517 |
| 7 | Radewoosh | 3410 |
| 8 | hos.lyric | 3399 |
| 9 | ecnerwala | 3392 |
| 9 | Um_nik | 3392 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 169 |
| 2 | maomao90 | 162 |
| 2 | Um_nik | 162 |
| 4 | atcoder_official | 161 |
| 5 | djm03178 | 158 |
| 6 | -is-this-fft- | 157 |
| 7 | adamant | 155 |
| 8 | awoo | 154 |
| 8 | Dominater069 | 154 |
| 10 | luogu_official | 150 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Dec/22/2024 09:16:45 (j1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|



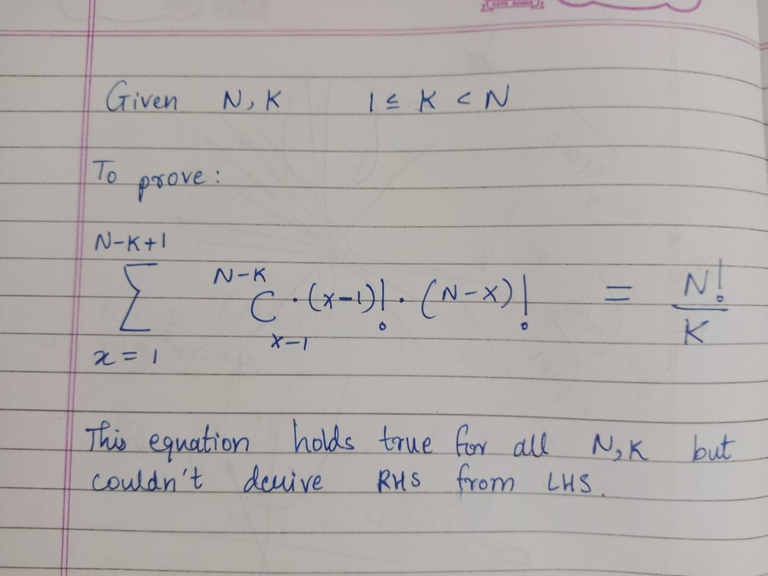







$$$\sum_{x=1}^{n-k+1} \frac{(n-k)!}{(x-1)!(n-k-x+1)!} . (x-1)!(n-x)!$$$
$$$= (n-k)!(k-1)! \sum_{x=1}^{n-k+1} \frac{(n-x)!}{(k-1)!(n-x-(k-1)!}$$$
$$$= (n-k)!(k-1)! \sum_{x=1}^{n-k+1} \binom{n-x}{k-1}$$$
$$$\sum_{x=1}^{n-k+1} \binom{n-x}{k-1} = \binom{n-1}{k-1} + \binom{n-2}{k-1} + .... + \binom{k-1}{k-1} = \binom{n}{k}$$$ (Repeatedly using $$$\binom{n+1}{r} = \binom{n}{r-1} + \binom{n}{r}$$$ on last 2 elements)
$$$=> LHS = \binom{n}{k} . (n-k)!(k-1)! = \frac{n!}{k}$$$
Reminded me of my JEE days
It is always nice to find combinatorial proofs for such equations.
Here's my proof.
Suppose $$$S = \sum_{x=1}^{n-k+1} \binom{n-k}{x-1} \cdot (x-1)! \cdot (n-x)!$$$
$$$S$$$ denotes the number of permutations $$$p$$$ of $$$[1,2,3, \ldots n]$$$ such $$$pos(p, 1) < \min\limits_{i = n-k+2}^{n} pos(p, i)$$$, where $$$pos(p, e)$$$ denotes the index at which the element $$$e$$$ is present in $$$p$$$($$$p_{pos(p, e)}=e$$$).
In other words, $$$S$$$ denotes the number of permutations of $$$[1,2,3, \ldots n]$$$ in which the element $$$1$$$ is present before $$$n-k+2, n-k+3, \ldots n$$$.
Consider an empty array $$$b$$$. First choose an integer $$$x$$$ among $$$[1,2, \ldots n-k+1]$$$. Select $$$x-1$$$ elements from $$$[2, 3, \ldots n-k+1]$$$. We have $$$\binom{n-k}{x-1}$$$ ways to select them. First, we append these $$$x-1$$$ elements to $$$b$$$ in any arbitrary order. We have $$$(x-1)!$$$ ways to do that. Now append $$$1$$$ to $$$b$$$. $$$n - x$$$ elements are remaining. We can insert them in any order. So there are $$$(n-x)!$$$ ways to append them. Thus for some $$$x$$$, we can get $$$\binom{n-k}{x-1} \cdot (x-1)! \cdot (n-x)!$$$ distinct permutations $$$b$$$. So, the total number of distinct permutations that we can get is $$$\sum_{x=1}^{n-k+1} \binom{n-k}{x-1} \cdot (x-1)! \cdot (n-x)!$$$.
Now, let us look for an easy way to find $$$S$$$. Consider an empty set $$$X$$$. We will insert permutations of length $$$n$$$ into it. Let us traverse all the valid $$$S$$$ permutations. For each permutation $$$b$$$, we will first insert $$$b$$$ into $$$X$$$. For each $$$i$$$ from $$$n-k+2$$$ to $$$n$$$, let $$$c$$$ be the permutation if we swap $$$1$$$ and $$$i$$$ in original $$$b$$$. Insert $$$c$$$ into $$$X$$$. For each $$$b$$$, we will insert $$$k$$$ distinct permutations.
It is not hard to observe that $$$X$$$ will finally contain all the $$$n!$$$ distinct permutations, and no permutation would have been inserted more than once.
So we get $$$S \cdot k = n!$$$.
Thus $$$S = \frac{n!}{k}$$$
where can i start if i'd like to learn proofs?
Thanks all...