Hi everyone!
Quite recently, a problem named Palindromes in Deque was added to the Library Checker that asks you to execute the following:
- Add a character $$$c$$$ to the beginning or the end of a string $$$s$$$;
- Remove a character from the beginning or the end of $$$s$$$.
In-between the queries you also need to maintain the number of distinct palindromes, and the size of the largest prefix- and suffix-palindromes of the current string.
The problem on Library Checker uses the approach from Double-Ended Palindromic Trees article by, presumably, liouzhou_101. The paper is quite long though, so after briefly looking through introduction part to familiarize myself with their main concepts, I decided to do something a bit different than they did. In this blog, I will explain my approach.
Recap
First, let's briefly recall what an eertree is.
If we consider all palindromes in a string $$$S$$$, we can organize them in two trees (for odd and even lengths, collectively called eertree), such that for a palindrome $$$T$$$, its children are all palindromes of form $$$cTc$$$ for any character $$$c$$$ that occur in the string.
Besides root vertices, the eertree of $$$S$$$ only has at most $$$n$$$ vertices, where $$$n = |S|$$$. This is due to the fact that whenever we add a letter $$$c$$$ to $$$S$$$, all potentially new palindromes are suffixes of $$$Sc$$$. At the same time, if one palindrome is a suffix of another, it also occurs in it as a prefix, meaning that among all suffix-palindromes of $$$Sc$$$, only the largest one is potentially new, compared to the set of palindromes of $$$S$$$.
The eertree also maintains a suffix link for each vertex, such that the suffix link of a palindrome $$$T$$$ is the largest suffix-palindrome of $$$T$$$. To put up an example, let $$$T = abacaba$$$, then the suffix link of $$$T$$$ would be $$$\operatorname{link}(T) = aba$$$.
Palindromes on stack
Consider the problem MMCC '15 P3 — Momoka, in which there is an additional constraints that we only ever append or pop characters at the back of the string. This variant of the problem is solved fairly simple, as you may maintain the stack of maximal suffix-palindromes for each prefix, and then pop states from the stack as you remove characters.
You also have to add letters in non-amortized time, which is doable
- in $$$O(\Sigma)$$$ by keeping a separate suffix link $$$\operatorname{link}(T, c)$$$ for each character $$$c$$$;
- in $$$O(\log n)$$$ by using "quick links" or "series links" from original eertree paper;
- in $$$O(\log \Sigma)$$$ by maintaining $$$\operatorname{link}(T, c)$$$ as a "persistent array".
Using the first approach, we arrive at a fairly simple and short implementation:
Now, how we can enhance this to maintain eertree on deque?
Palindromes on deque
Essentially, what we need is in one way or another be able to find the largest prefix-palindrome or the largest suffix-palindrome of a string after each operation. It may be tempting to try maintaining two stacks, one for suffix-palindromes of all prefixes, and another for prefix-palindromes of all suffixes. Unfortunately, largest prefix-palindromes of all suffixes may change a lot when we change the last character of the string. Conversely, largest suffix-palindromes of all prefixes may change a lot when we change the first character of the string.
When we maintained eertree on a stack, we additionally maintained a stack of certain states. It would be only natural to now maintain a single deque of states when we try to maintain eertree on a deque. But what kind of states do we need? If we think about maximal suffix- or prefix-palindrome, a natural way to rephrase the definition would be: a maximal palindrome that is not a prefix/suffix of another palindrome.
That being said, we can take one of the following two approaches:
- "surfaces", aka palindromic substrings that are neither a prefix, nor a suffix of another palindrome;
- "maximal palindromes", aka palindromes substrings that are not contained in any other palindromic substring.
If we consider these sets of palindromic strings, maximal prefix/suffix palindromes of the whole string will always be among them. While the paper on arxiv maintains the structure of surfaces, I felt like it's not the most natural approach, because they don't seem to form a natural deque structure. But maximal palindromes do! Indeed, no two maximal palindromes may share their center, thus we can maintain them in a deque, ordered by their center position. More importantly, only $$$O(1)$$$ of them change when we append or remove a letter on any side.
Maximal palindromes deque
Let $$$\operatorname{par}(cTc) = T$$$, that is $$$\operatorname{par}$$$ leads from $$$T$$$ to its parent in the eertree.
When we add a new character to either side of the eertree, we always create a new maximal palindrome that occurs at that side of the string as a maximal prefix/suffix palindrome. Let this new palindrome be called $$$last$$$.

$$$last$$$ covers previous occurrence of $$$\operatorname{par}(last)$$$
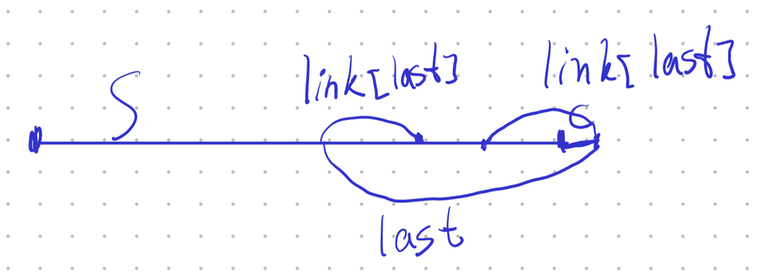
$$$last$$$ covers previous occurrence of $$$\operatorname{link}(last)$$$
At the same time, due to the addition of $$$last$$$ into the deque, we might need to remove at most two other maximal palindromes from the deque. These palindromes can only correspond to $$$\operatorname{par}(last)$$$, if it was the previous maximal prefix/suffix palindrome at that end of the string and is now consumed by $$$last$$$, or it can be $$$\operatorname{link}(last)$$$, namely its occurrence as the prefix of $$$last$$$.
Any other substring-palindrome of $$$last$$$ would be either its suffix-palindrome or prefix-palindrome, meaning that as a suffix-palindrome, it was only added right now, and couldn't have already been in the deque, and the prefix-palindrome could only be in the deque if it was $$$\operatorname{link}(last)$$$, any other prefix-palindrome would be included in $$$\operatorname{link}(last)$$$, and thus would not be covered. And all the other sub-palindromes of $$$last$$$ must also be sub-palindromes of $$$\operatorname{par}(last)$$$, so the similar reasoning applies to them.
Maintaining the deque
The results above tell us that, in essence, we can implement the operations as follows:
- Push: Find $$$last$$$, remove maximal palindromes at the corresponding end of the deque while they're covered by $$$last$$$;
- Pop: Remove $$$last$$$ from the end of the deque, add $$$\operatorname{link}(last)$$$ and $$$\operatorname{par}(last)$$$ if they're not covered by the palindromes in the deque.
Sounds simple enough, except for how do we check if two maximal palindromes cover one another?
So far, we only assumed that we store a deque of state indices, but this information is insufficient to check whether one occurs in the other. So, we need to store some kind of information about their relative positioning to each other. Moreover, we want our implementation to be uniform for doing things on either side, so we need this information to be meaningful both when it's read left-to-right and right-to-left.
To achieve this symmetry, we can not base our positioning on the positions of left or right ends of the substrings, as it would imply different things when read left-to-right or right-to-left. However, as we already mentioned, we maintain the deque of the maximal palindromic substrings, ordered by the position of their center. Well, that's it! We will keep a second deque that will store the distance between the middles of the neighboring maximal palindromes. Let's see how it works.
Assume that last two palindromes in the deque are $$$pre$$$ and $$$last$$$. We know $$$\operatorname{len}(pre)$$$ and $$$\operatorname{len}(last)$$$, and we know that $$$last$$$ occurs as a prefix/suffix of the whole string. So, if we count from the corresponding end of the string, $$$last$$$ starts at $$$0$$$ and ends at $$$\operatorname{len}(last)$$$. To check if it covers $$$pre$$$, let $$$m$$$ be the distance between farther end of $$$pre$$$ from the end of the string. We need to check whether $$$m \leq \operatorname{len}(last)$$$.
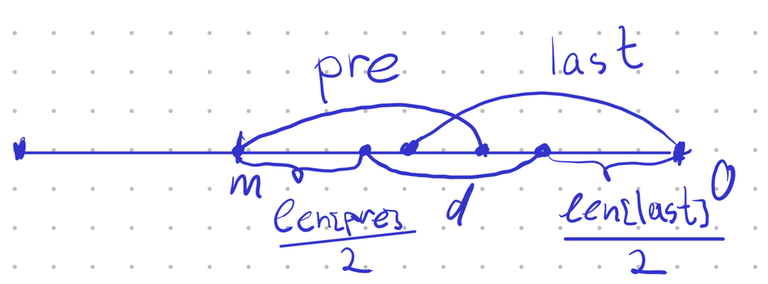
Finding $$$m$$$ from $$$d$$$
To check this, we need to express $$$m$$$ as a function of $$$\operatorname{len}(last)$$$, $$$\operatorname{len}(pre)$$$ and $$$d$$$, which is the distance between centers of $$$pre$$$ and $$$last$$$.
On the picture above, we can see that
or, equivalently,
where $$$D = 2d$$$ is the double distance between the middles. So, the condition of being nested rewrites as $$$\operatorname{len}(pre) + D \leq \operatorname{len}(last)$$$.
Note that we can also find the doubled distance between the centers of
- $$$last$$$ and $$$\operatorname{par}(last)$$$ as $$$0$$$,
- $$$last$$$ and $$$\operatorname{link}(last)$$$ as $$$\operatorname{len}(last) - \operatorname{len}(\operatorname{link}(last))$$$,
- $$$last$$$ and $$$pre$$$ as $$$2 + \operatorname{len}(pre) - \operatorname{len}(last)$$$.
Altogether, this leads to a fairly concise symmetric implementation that can be found e.g. in this submission.











Thanks sir. Loved it. Very useful.
how can i be strong like you?
++
This must be the most cursed serious blog title I've ever seen in codeforces.
very helpful.
OYZ
OYZ? tell him to put some pants on
Where would he find his pants when cp competitions only give out tshirts?
Double-ended neelbuod
The only real application of palindromes
what does neelbuod mean
drawkcab daer
are there more applications of palindromes?
are there more applications of palindromes?
Excellent
are there more applications of palindromes?
These Elden Ring references are getting out of hand.
Really good explanation