Neeki's blog

Graph theory problem
By Neeki, history, 6 months ago, In English

Given a graph G s.t. any cycle in G has length 3.
1)Find the maximum number of edges. 2)Find the maximum number of cycles.

  • Vote: I like it
  • +6
  • Vote: I do not like it

»
6 months ago, # |
  Vote: I like it -38 Vote: I do not like it
  1. What does this mean?
  2. You can do a brainless $$$O(\frac{nm}{w})$$$ solution using bitsets. Do you need something faster?
→ Reply
»
6 months ago, # |
← Rev. 2   Vote: I like it +9 Vote: I do not like it

number of cycles is floor(n/3), number of edge floor(n/3)*3 + n-(floor(n/3)*3)+(floor(n/3)-1) it will graph n3 simple loops and bridges?

→ Reply
»
6 months ago, # |
← Rev. 2   Vote: I like it +9 Vote: I do not like it

Edit: The following is not quite correct. Check the comment below from nor and the continuation.

Imagine starting with a tree. It has $$$N$$$ nodes and $$$N - 1$$$ edges. Now expand each node into a cycle of 3 nodes. You get $$$3N$$$ nodes and $$$4N - 1$$$ edges. So the number of edges for a graph with $$$3N$$$ nodes is $$$4N - 1$$$. When you remove one or two nodes, you have to break at most one cycle, thus you can get for a graph with $$$3N - 1$$$ nodes the maximum number of edges is $$$4N - 3$$$ and for $$$3N - 2$$$ nodes you have at most $$$4N - 4$$$ edges.

This I believe can be proven by an argument similar to the following:

Any two "adjacent" cycles must be connected through precisely one node. If there were two connections then there would be a cycle of length greater than 3. This structure looks like a tree, where each node is what you get when you contract each cycle to a node. Then if you focus on the tree, you get the thing above.

I am aware that it is not quite a proof, but I don't know how to state it.

For the second question, the answer is $$$\lfloor\frac{N}{3}\rfloor$$$. You can get it using a similar argument, any 3 nodes can be in at most one cycle.

→ Reply
  • »
    »
    6 months ago, # ^ |
      Vote: I like it +2 Vote: I do not like it

    The answer to the second question can be larger than $$$\lfloor N/3 \rfloor$$$. Consider a linear chain of $$$k+1$$$ nodes, and add another $$$k$$$ nodes such that the $$$i$$$-th and $$$i+1$$$-th nodes in the first set are joined to the $$$i$$$-th node in the second set. You have $$$k$$$ cycles with only $$$2k+1$$$ nodes.

    This same graph seems to provide a counterexample for the first claim too, since you have $$$3k$$$ edges with only $$$2k+1$$$ nodes.

    → Reply
    • »
      »
      »
      6 months ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Thanks for the heads up

      I assumed that such a construction would not be valid since we can find a walk that does not use the same edge twice and returns to the start and has length $$$>3$$$. I have not consulted the official definition of a cycle (which I am guilty of doing).

      Using the right definition we can see that in the tree of cycles, every edge that connects two cycles can be removed, having the two adjacent nodes get merged. This reduces the number of nodes to $$$3N - (N - 1) = 2N+1$$$ and the number of edges to $$$4N-1-(N-1)=3N$$$, which is also your construction.

      This also means that the answer for the second problem is $$$\lfloor \frac{N-1}2 \rfloor$$$ if $$$N > 0$$$

      → Reply
»
6 months ago, # |
  Vote: I like it 0 Vote: I do not like it

since there is no restriction that the graph has to be connected, the union of $$$\frac N 3$$$ triangles would have $$$N$$$ edges (and $$$\frac N 3$$$ triangles).

→ Reply
»
6 months ago, # |
← Rev. 4   Vote: I like it 0 Vote: I do not like it

if i understand your question correctly the answer of your first question is $$$\lfloor \frac{n-1}{2} \rfloor+n-1$$$ and the answer of your second question is $$$\frac{n-1}{2}$$$ example for both of them is that you connect vertex $$$(u,v)$$$ if $$$u=v-1$$$ or ($$$u=v-2$$$ && $$$ u \equiv 0 \pmod{2} $$$) (We number the vertices from 0 )like this picture $$$(n=9)$$$:$$$\newline$$$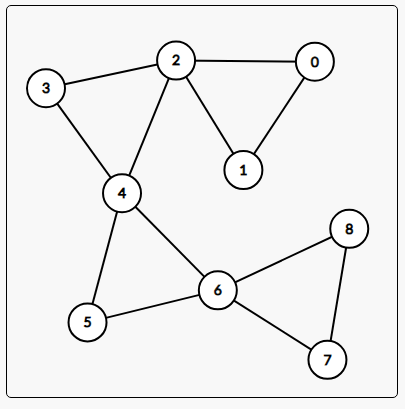 $$$\newline$$$ and we can prove first question with bfs if we run bfs from vertex $$$ u $$$ We know that a vertex cannot have 2 neighbors in the previous layer (fact 1) Because if it has We know that those two vertices have a path length of more than 1(in previous layers), so despite this vertex and the two edges it has. We will have a cycle longer than 3 and also if a vertex have $$$x$$$ child in our bfs we know that all edge between them (include between childs) can be at most $$$x+\lfloor \frac{x}{2} \rfloor $$$ because we know that in children we can't have a path with length larger than 1 . so at most we have $$$\lfloor \frac{x}{2} \rfloor$$$ edges between them . and we have at most $$$x$$$ edge between this vertex and its childs because it has $$$x$$$ child $$$\newline$$$ now with fact 1 we have : $$$\sum child_i \le n-1$$$ (it can be disconnect) so we proved that we have at most $$$\lfloor \frac{n-1}{2} \rfloor+n-1$$$ edges $$$\newline$$$ For your second question, you can prove it with dfs in a simple way (count the back edge) Finally, sorry if my English is not good

→ Reply
  • »
    »
    6 months ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I forgot to mention this fact: In bfs, for this question, there aren't any two vertices that are in the same layer and do not have a common parent and have an edge between them, because in this case we have a cycle with a length greater than 3.

    → Reply
»
6 months ago, # |
  Vote: I like it 0 Vote: I do not like it

This was a question in the endsem exam of discrete structures course i did a year ago. Still dont know how to solve it :(

→ Reply