Подскажите как решить такую задачу(http://www.e-olimp.com.ua/ru/problems/3507) с помощью дерева отрезков. Что хранить в вершине? Как прибавлять?
→ Обратите внимание
До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
19:02:20
Зарегистрироваться »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
19:02:20
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 22.11.2024 22:32:42 (l2).
Десктопная версия, переключиться на мобильную.
При поддержке
эту задачу можно решить не только деревом отрезков, но и с помощью дп.
Извините, Вы видимо видели старый вариант блога(случайно перепутал ссылки).
А, ну в этом случае Вам понадобится прибавление и обновление на отрезке. В вершине хранить 1 если на этом отрезке есть участок высоты X, и 0 в противном случае. И для каждого запроса "?" узнавать сумму на отрезке. Если сумма >0 то YES, иначе NO.
Если бы это было обычное прибавление на отрезке, а не прибавление на отрезке с поиском елемента, то я бы не создал этот блог.
неверная идея
А если мы например на подотрезке 0-1 добавили одно число, на подотрезке 2-3 добавили другое, а запрос пришел на подотрезок 0-3? Придется спускаться и проверять и там и там. Это уже будет не логарифм. Может, я что-то неверно понял?
В худшем случае мы посетим log вершин в ДО, в каждой мы можем делать поиск за log, т.е за log^2 — на запрос.
Нет, в худшем будет уже не log, что я и пытаюсь объяснить. Допустим, мы добавили 1 на отрезке 0..1, 2 на 2..3, 3 на 4..5 (...) n / 2 на n-2..n-1. Теперь пришел запрос "есть ли число X на отрезке 0..n-1". Придется спускаться в n / 2 вершин дерева отрезков и в каждой отдельно проверять.
Да, вы правы. Я это не учел.
в худшем случае мы посетим log вершин ДО, и каждую придется перестраивать — это займет O(n) времени.
Поэтому в вершинах надо хранить не мультисеты, а декартовы деревья — вот тогда действительно получится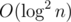
на запрос
Но как тогда быть в таком случае: Прибавить на отрезке 1..5 значение 2 Прибавить на отрезке 6..10 значение -8 Найти что-то на отрезке 1..10 Что делать в таком случае?
Эта задача решается корневой с хэш-мепом, разбиваем массив на корень отрезков для каждого из них храним хэш-меп и число на сколько нужно увеличить отрезок, изначально 0. При запросе увеличении нужно пройтись по массиву отрезков в корневой, когда отрезок полностью входит в отрезок, который нужно увеличить, то просто увеличить число на которое нужно увеличить, если же не полностью, то чистим хэш-меп этого отрезка и заново закидываем все числа, которые должны быть в этом отрезке. На запрос нахождения числа, нужно пройтись по массиву отрезков и посмотреть, если отрезок полностью входит в отрезок на котором нужно посмотреть есть ли число, то посмотреть в хэш-мепе есть ли число x — Inc(b), x — число, которое нужно найти, Inc(b) — число, на которое нужно увеличить отрезок, если же не полностью, то проходим по этому отрезку и смотрим есть ли число или нет. Как-то криво получилось написать идею, но такое решение должно зайти.
Эта задача на дерево отрезков, где в каждой вершине мы храним отсортированный массив.
Об этом можно прочитать здесь. Эта структура позволяет отвечать на следующий запрос: есть ли на отрезке число x (за log ^ 2 или за log).
Осталось научиться прибавлять на отрезке. Для этого просто храним в каждой вершине значение сколько мы прибавили в ней (никаких пушей делать не надо). Назовем это значение plus И потом когда спускаемся по дереву надо делать x -= v -> plus; И искать на отрезке x.
Написал криво, но надеюсь суть ясна
То что Вы описали не сработает на таком тесте: 5 1 2 3 4 5 Отнять на отрезке {1..3} число 3 Найти на отрезке {1..5} число 0
Ваш алгоритм 0 не найдет, хотя он есть на отрезке...
Да действительно, я написал чушь
Можно SQRT декомпозицией решить. Разбить массив на блоки, ну и хранить в блоке на сколько мы уже изменили все элементы внутри. Если запрос не полностью покрывает блок, то можно поступить так: Храним еще и стартовый массив , а внутри блока вместо массива используем std::set. Если запрос прибавления покрывает весь блок, то храним в блоке сколько мы уже добавили к этому блоку.Тогда, когда запрос частично задевает блок, и на всем блоке мы уже изменили элементы на X то идем по стартовому массиву, и заменяем в set-е стартовое число a[i]+x на новое, а в стартовый массив заносим "новое — x" число. Итоговая асимптотика — N*sqrt(N)*lg(N). За 3 секунды такое должно зайти.