Hi everyone,
I've been working on a problem involving weighted directed graphs and could use some help. The problem is as follows:
Problem Statement:
I have a weighted directed graph which may or may not contain cycles, and it can have multiple cycles. The nodes are 1-based indexed. I need to create an array cycleSum of size equal to the number of nodes. For each node i, cycleSum[i] should contain the sum of the weights of the smallest cycle in which node i is a part of. If a node is not part of any cycle, cycleSum[i] should be -1. If a node is part of multiple cycles, the array should contain the sum of weights of the cycle with the minimum sum. Example:
Node 1: Cycle 1 (weight 10)
Node 2: Cycle 1 (weight 10), Cycle 2 (weight 20)
Node 3: No cycle
cycleSum = [10, 10, -1]
Approach: I want to solve this problem using Depth-First Search (DFS). However, I'm having trouble figuring out how to correctly detect cycles and calculate the minimum cycle sum for each node.
My Questions:
How can I efficiently detect cycles in a directed graph using DFS? How should I keep track of the cycle sums and update cycleSum array with the minimum cycle sum for each node? Are there any specific edge cases I should be aware of?
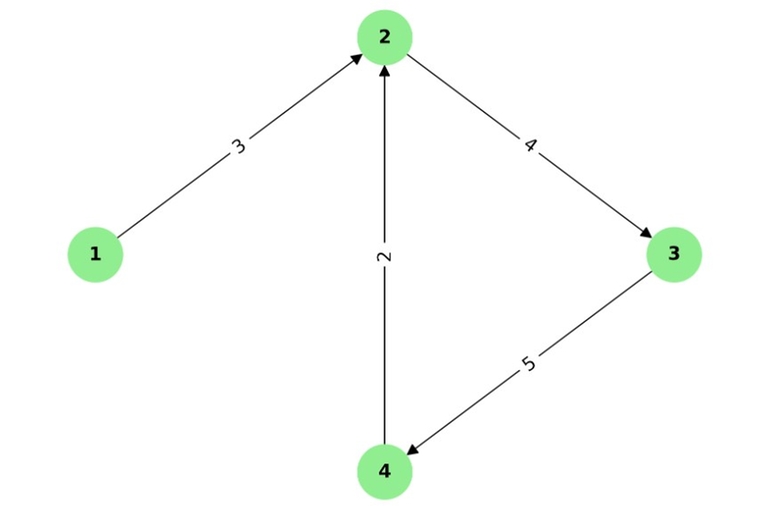
Node 1: Not part of any cycle cycleSum: -1
Node 2: Part of the cycle: 2 -> 3 -> 4 -> 2 Cycle sum: 4 + 5 + 2 = 11
Node 3: Part of the cycle: 3 -> 4 -> 2 -> 3 Cycle sum: 5 + 2 + 4 = 11
Node 4: Part of the cycle: 4 -> 2 -> 3 -> 4 Cycle sum: 2 + 4 + 5 = 11
So, the cycleSum array should be: cycleSum = [-1, 11, 11, 11]
I would appreciate any guidance or suggestions on how to approach this problem. Thanks in advance for your help!










