Problem statement A series of highways connect n cities numbered from 0 to n — 1. You are given a 2D integer array highways where highways[i] = [city1i, city2i, tolli] indicates that there is a highway that connects city1i and city2i, allowing a car to go from city1i to city2i and vice versa for a cost of tolli. You are also given an integer discounts which represents the number of discounts you have. You can use a discount to travel across the ith highway for a cost of tolli / 2 (integer division). Each discount may only be used once, and you can only use at most one discount per highway. Return the minimum total cost to go from city 0 to city n — 1, or -1 if it is not possible to go from city 0 to city n — 1.
Example 1: Input: n = 5, highways = [[0,1,4],[2,1,3],[1,4,11],[3,2,3],[3,4,2]], discounts = 1 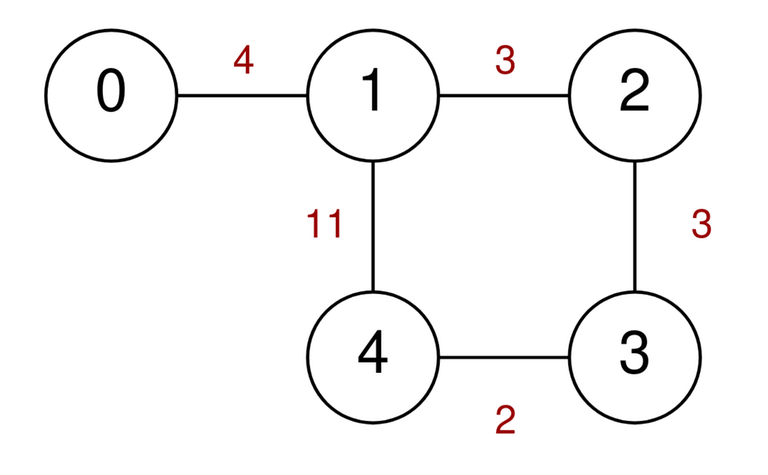 Output: 9 Explanation: Go from 0 to 1 for a cost of 4. Go from 1 to 4 and use a discount for a cost of 11 / 2 = 5. The minimum cost to go from 0 to 4 is 4 + 5 = 9.
Output: 9 Explanation: Go from 0 to 1 for a cost of 4. Go from 1 to 4 and use a discount for a cost of 11 / 2 = 5. The minimum cost to go from 0 to 4 is 4 + 5 = 9.
Time complexity As per my understanding Time complexity for this would be k * E log (V * k). Since Each edge can be reached with k different number of discount values and with decreased toll value everytime (k * E) and also this means each vertex may be present in heap k number of times (log(V * k)). Here K is the number of discounts. Is it correct ?











Auto comment: topic has been updated by acash (previous revision, new revision, compare).
make two identical graph G(u,v) and G'(u,v) such that G'(u,v) initialize to G(u,v) now for edge E(u,v) make and from node u to v with weight w/2 where u belongs to G and v belongs to G' now apply dijkstra's shortest path algorithm from node 0 and find distance of node n-1 of graph G' here is code for this problem
this is for discount = 1 if you have k number of coupons then make k+1 copies of graph
k is not required inside log as far I understand your solution
See this Click
Could you guys Please help with time complexity of this ? indresh_hErd ANIKET_IITB
I think k also come in log as well because basically we are making k copies of original graph so TC: k(E+V)log(kE)
why log(KE) ? We always insert vertex in heap a vertex can be relaxed with k different values or in other words we end up visting the same vertex with k different values. So a vertex can be present inside heap k number of times and for all vertex it is v*k shouldn't it be log(v*k) ?
we don't insert vertex in heap we insert touple ( vertex ,weight) in heap. vertex can come again in heap with different weight. so Log(EK) will come
Yes I agree with you log(kV) is correct
Regarding aniket's explanation altough we are inserting tuple but the unqiue component in it is the vertex and vertex will atmost k times as explained by you
Djikstra