Consider rotating coordinate plane by $$$45$$$ degrees when you encounter Manhattan distance problem
Before I learned this trick, I had heard this phrase several times, but I never understood what it means. Turns out it is a pretty cool and easy trick. In this blog, I explain the trick in $$$2$$$ different ways, and show how to use it in practice on one of the recent problems. I tried to make this blog approachable, tested it on a $$$1200$$$~ rated participant
Let's look at this problem. I recommend thinking about it on your own for $$$10$$$-$$$15$$$ minutes.
Summary of the statement: you are given n = $$$2e5$$$ points. You have to find $$$3$$$ points, so that the Manhattan distance between each pair is d ( d is always even). Definition of Manhattan distance: $$$dist = |x_1 - x_2| + |y_1 - y_2|$$$
The solution above, in my opinion, is not trivial to think of neither to implement. But I think the trick in a way helps with both of the issues.
There are 2 ways to think about it, in a purely algebraic, or geometrical form. I suggest you read both of them.
The Algebra form:
It is a bit hard to work with the formula of Manhattan distance $$$dist = |x_1 - x_2| + |y_1 - y_2|$$$. It has 4 variables, and 2 summands of absolute values. Let's try to simplify it.
1) Let's start with introducing 2 new variables for convenience:
- $$$x_d = x_1-x_2$$$
- $$$y_d = y_1-y_2$$$
- $$$|x_1 - x_2| + |y_1 - y_2|$$$
<=>$$$|x_d| + |y_d|$$$
2) Let's divide our formula into 2 cases:
case where signs of $$$x_d$$$ and $$$y_d$$$ are the same (for this section I treat $$$0$$$ as positive number)
- if $$$\color{green}{(x_d \geq 0 \texttt{ and } y_d \geq 0) \texttt{ or } (x_d < 0 \texttt{ and } y_d < 0)}$$$ then: $$$|x_d| + |y_d|$$$
case where signs of $$$x_d$$$ and $$$y_d$$$ are the oposite:
- if $$$\color{green}{(x_d \geq 0 \texttt{ and } y_d < 0) \texttt{ or } (x_d < 0 \texttt{ and } y_d \geq 0)}$$$ then: $$$|x_d| + |y_d|$$$
For now part after " then " is the same, but in the next step we will transform both of them.
3) Under these 2 conditions we can put everything under one $$$abs()$$$ function.
When signs of $$$x_d$$$ and $$$x_y$$$ are the same, it is clear how to do it, just summarize them inside of the $$$abs()$$$ function.
- when $$$\color{green}{(x_d \geq 0 \texttt{ and } y_d \geq 0) \texttt{ or } (x_d < 0 \texttt{ and } y_d < 0)}$$$ : $$$|x_d| + |y_d| = |x_d + y_d|$$$
And if the signs are different, let's make them the same, and then summarize them.
- when $$$\color{green}{(x_d \geq 0 \texttt{ and } y_d < 0) \texttt{ or } (x_d < 0 \texttt{ and } y_d \geq 0)}$$$ : $$$|x_d| + |y_d| = |x_d + (-y_d)| = |x_d - y_d|$$$
4) Now the most interesting part: let's try combining conditions together once again.
So we know that we can use the formula $$$|x_d + y_d|$$$ when signs of $$$x_d$$$ and $$$y_d$$$ are the same. But what happens to it when the signs are opposite?
We can see that $$$(|x_d + y_d| \color{red}{=} |x_d| + |y_d|)$$$ no longer holds true. To be more specific:
- when $$$\color{green}{(x_d \geq 0 \texttt{ and } y_d < 0) \texttt{ or } (x_d < 0 \texttt{ and } y_d \geq 0)}$$$ : $$$|x_d + y_d| \leq |x_d| + |y_d|$$$
We can make a similar statement with formula $$$|x_d - y_d|$$$: when signs of $$$x_d$$$ and $$$y_d$$$ are the same, the following is true:
- when $$$\color{green}{(x_d \geq 0 \texttt{ and } y_d \geq 0) \texttt{ or } (x_d < 0 \texttt{ and } y_d < 0)}$$$ : $$$|x_d - y_d| \leq |x_d| + |y_d|$$$
We can make a very interesting conclusion:
When signs are the same:
- $$$|x_d - y_d| \leq |x_d| + |y_d|$$$.
- $$$|x_d + y_d| = |x_d| + |y_d|$$$
- That means that $$$|x_d - y_d| \leq |x_d + y_d|$$$
- when $$$\color{green}{(x_d \geq 0 \texttt{ and } y_d \geq 0) \texttt{ or } (x_d < 0 \texttt{ and } y_d < 0)}$$$ : $$$|x_d - y_d | \leq |x_d + y_d|$$$
When signs are the opposite:
- $$$|x_d + y_d| \leq |x_d| + |y_d|$$$.
- $$$|x_d - y_d| = |x_d| + |y_d|$$$
- That means that $$$|x_d + y_d| \leq |x_d - y_d|$$$
- when $$$\color{green}{(x_d \geq 0 \texttt{ and } y_d < 0) \texttt{ or } (x_d < 0 \texttt{ and } y_d \geq 0)}$$$ : $$$|x_d + y_d | \leq |x_d - y_d|$$$
5) Now we have everything in place. Let's summarize it in human words.
- We had a formula that we divided into 2 cases, depending on $$$x_d$$$ and $$$y_d$$$ having the same or the opposite sign.
- We understood that when signs are the same, we can use formula $$$|x_d + y_d|$$$, and when they are the opposite, we can use $$$|x_d - y_d|$$$
- When the signs are the same, that $$$|x_d + y_d|$$$ gets us the biggest result out of 2 formulas, and when they are the opposite |$$$x_d - y_d$$$| gives the biggest.
So:
- signs are the same: we want to use $$$|x_d + y_d|$$$ and it is bigger (or equal)
- signs are the opposite: we want to use $$$|x_d - y_d|$$$ and it is bigger (or equal)
We can make a conclusion that to combine this 2 formulas we can always take the biggest one, and it will be the one we want to use.
So we end up with this beautiful formula
- $$$max(|x_d+y_d|, |x_d-y_d|)$$$
6) Let's rewrite it in terms of $$$x$$$ and $$$y$$$
- $$$max(|x_1-x_2+y_1-y_2|, |x_1-x_2+y_2-y_1|)$$$
And shuffle it around
- $$$max(|(x_1+y_1) - (x_2+y_2)|, |(x_1-y_1) - (x_2-y_2)|)$$$
7) lets define 2 new variables $$$s=x+y$$$ , $$$t = x-y$$$, with these variables we get:
- $$$dist = max(|s_1-s_2|, |t_1-t_2|)$$$
8) One final thing we should understand is that this formula no longer uses $$$x$$$ or $$$y$$$. It means that we can calculate values $$$s$$$ and $$$t$$$ for each point and work only with them.
As you can see, the formula became a lot more pretty. And also we can look at it in an interesting way: the distance between 2 points can be caused by the difference in coordinate $$$s$$$ or $$$t$$$ (or it can be both). This property can be used to solve the problem above.
I suggest you try to think about this problem on your own for 10-15 minutes once again, you may see this problem in a different light.
Geometric form
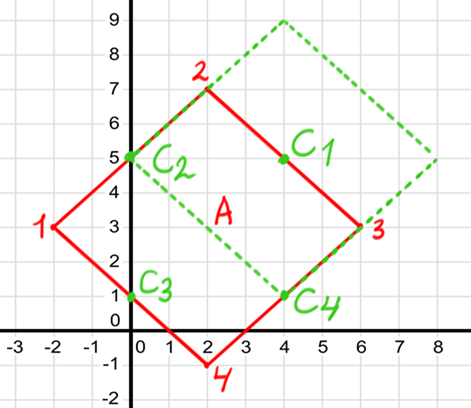
1) In the picture below you can see a random point $$$\color{#A00}{P}$$$ I chose. All points that are at a Manhattan distance of $$$3$$$ from point $$$\color{#A00}{P}$$$ are located on the red square. Also $$$\color{#A00}{W}$$$ represents one of the sides of the red square.
Notice that the red square is not parallel to $$$OX$$$ and $$$OY$$$ axes. Because of it is a bit hard to visualize how it looks without drawing.
But it should not necessarily be like that. Let's make a new coordinate system with axes $$$OS$$$ and $$$OT$$$, where sides of the square are parallel (or perpendicular) to the new axes. We can achieve that by having $$$OS$$$ go in $$$\vec{(1, 1)}$$$ direction, and $$$OT$$$ in $$$\vec{(1, -1)}$$$ direction.
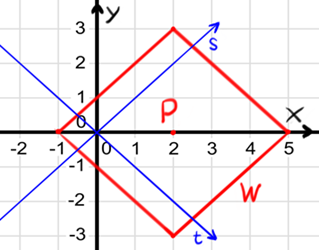
From this point I will use $$$black$$$ color to represent points in $$$XY$$$ system, and $$$\color{blue}{blue}$$$ color for $$$ST$$$ system.
2) Now let's think about the unit of measure, that we will use in our new $$$ST$$$ coordinate system. We will use $$$\color{blue}{(s, t)}$$$ notation to define points.
- Notice that side $$$\color{#A00}{W}$$$ has a distance to the point $$$(0, 0)$$$ equal to $$$3.5$$$ diagonals (of 1x1 squares). We don't want to deal with decimal numbers, so let's take as a unit of measure a half-diagonal.
- If we do that, point $$$(1, 1)$$$ in $$$XY$$$ system will be equal to $$$\color{blue}{(2, 0)}$$$ in $$$ST$$$ system
- And point $$$(1, -1)$$$ in $$$XY$$$ system will be equal to $$$\color{blue}{(0, 2)}$$$ in $$$ST$$$ system
Now we have everything ready to locate every corner of the red square and point $$$\color{#A00}{P}$$$ in our new $$$ST$$$ coordinate system.
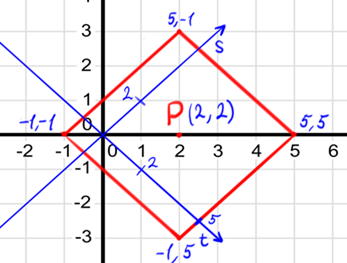
3) I think it is a good moment to learn how to transform points from $$$XY$$$ system to $$$ST$$$ system. To do that let's think in terms of vectors, I think it would be easier to understand this way.
One of the corners of the red square has coordinates $$$(2, 3)$$$ in $$$XY$$$ and coordinates $$$\color{blue}{(5, -1)}$$$ in $$$ST$$$. Let's try to make this transition between coordinate systems through formulas.
a) At first, lets understand how basis vectors of $$$XY$$$ $$$\vec{(1, 0)}$$$ and $$$\vec{(0, 1)}$$$ transfer to $$$ST$$$.
- $$$\vec{(1, 0)}$$$ in $$$XY$$$ looks like $$$\color{blue}{\vec{(1, 1)}}$$$ in $$$ST$$$
- $$$\vec{(0, 1)}$$$ in $$$XY$$$ looks like $$$\color{blue}{\vec{(1, -1)}}$$$ in $$$ST$$$
b) Then we should understand that any point can be described using basis vectors and origin point $$$(0, 0)$$$
So point $$$(2, 3)$$$ in $$$XY$$$ system can be described as
- $$$(0, 0) + 2 * \vec{(1, 0)} + 3 * \vec{(0, 1)} = (2, 3)$$$
c) And now the cool part: let's use the formula from b, but instead of using $$$XY$$$ coordinates for basis vectors, let's use their $$$ST$$$ coordinates that we got in a
- $$$\color{blue}{(0, 0)} + 2 * \color{blue}{\vec{(1, 1)}} + 3 * \color{blue}{\vec{(1, -1)}} = \color{blue}{(5, -1)}$$$
So the point $$$(2, 3)$$$ in $$$XY$$$ system converts to $$$\color{blue}{{(5, -1)}}$$$ in $$$ST$$$
It's a hustle to go though all of these operations every time we want to transfer a point from $$$XY$$$ to $$$ST$$$, so we should put all of the above into simple formula.
We can think about it like this:
- For every $$$1$$$ in $$$x$$$ coordinate, we add $$$1$$$ to $$$s$$$ and $$$1$$$ to $$$t$$$ (because basis vector $$$\vec{(1, 0)}$$$ in $$$XY$$$ translates to $$$\color{blue}{\vec{(1, 1)}}$$$ in $$$ST$$$
- For every $$$1$$$ in $$$y$$$ coordinate, we add $$$1$$$ to $$$s$$$ and $$$-1$$$ to $$$t$$$ (because basis vector $$$\vec{(0, 1)}$$$ in $$$XY$$$ translates to $$$\color{blue}{\vec{(1, -1)}}$$$ in $$$ST$$$
We can summarize it as
- $$$s = x + y$$$
- $$$t = x - y$$$
Notice that we had variables $$$s$$$ and $$$t$$$ in the algebra section that we defined exactly like that.
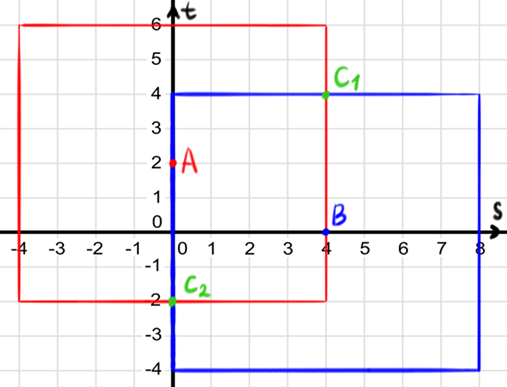
4) So now we know how to convert points from $$$XY$$$ to $$$ST$$$, but it does not help us yet. Let's redraw a picture, get rid of $$$XY$$$ coordinate system (we won't need it anymore) and make $$$OS$$$ go to the right, and $$$OT$$$ go up.
- Note that we can point the axes in any direction, I usually use $$$(s,t)$$$ notation, so I want the first coordinate to point to the right, and the second one — up, so it behaves just like regular $$$XY$$$ coordinate system with points written in $$$(x, y)$$$ notation
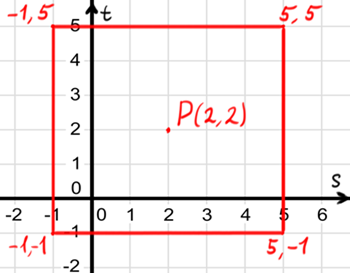
5) Now interesting things start to happen: remember that red square still represents the Manhattan distance from $$$P$$$ equal to $$$3$$$, but now it looks different. Manhattan distance formula should also look different, it should represent a square that is parallel to axes $$$S$$$ and $$$T$$$. We can try to deduce what formula it will be by analyzing the picture above.
a) At first, let's try to describe the square the most straightforward way
- $$$s = 5, -1 \leq t \leq 5$$$
- $$$s = -1, -1 \leq t \leq 5$$$
- $$$t = 5, -1 \leq s \leq 5$$$
- $$$t = -1, -1 \leq s \leq 5$$$
b) let's try to simplify equation $$$-1 \leq t \leq 5$$$
- $$$-1 \leq t \leq 5$$$
<=>$$$-3 \leq t-2 \leq 3$$$<=>$$$|t-2| \leq 3$$$ - the same goes for $$$s$$$ : $$$|s-2| \leq 3$$$
Let's right down simplified formula
- $$$s = 5, \color{green}{|t-2| \leq 3}$$$
- $$$s = -1, \color{green}{|t-2| \leq 3}$$$
- $$$t = 5, \color{green}{|s-2| \leq 3}$$$
- $$$t = -1, \color{green}{|s-2| \leq 3}$$$
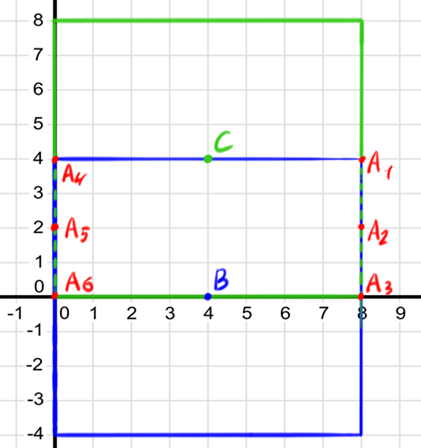
c) We should think about combining the statements together.
- $$$s = 5 \texttt{ or } s = -1$$$
<=>$$$|s-2| = 3$$$ - $$$t = 5 \texttt{ or } t = -1$$$
<=>$$$|t-2| = 3$$$
so we get this:
- $$$\color{green}{|s-2| = 3}$$$, $$$|t-2| \leq 3$$$
- $$$\color{green}{|t-2| = 3}$$$, $$$|s-2| \leq 3$$$
I think here it is clear that we can use $$$max$$$ function to combine these $$$2$$$ statements
- $$$max(|s-2|, |t-2|) = 3$$$
Values $$$(2, 2)$$$ represent coordinates of the point $$$P$$$ in $$$ST$$$ system.
- $$$max(|s-s_P|, |t-t_P|) = d$$$.
So the general formula will look like this:
- $$$d = max(|s_1-s_2|, |t_1-t_2|)$$$.
Notice that it is the exact same formula that we got in the algebra section of the blog.
From this point we can follow the editorial for the algebra approach. Or we can be more interesting: let's try to solve the problem above with visual approach (just like we did in the editorial without the trick), but this time it will be a bit different: because we don't have to deal with diagonals, the implementation will be much easier.
And also, but this is just my opinion, I find it a bit easier to come up with this approach while using the trick, I only thought of this solution after thinking in terms of $$$ST$$$ coordinates. I know that there is little difference, but I find it a lot easier to imagine it in my head.
Conclusion
I think that the approaches I provided for the problem above are not that difficult, but that task was marked as $$$\color{red}{2400}$$$ problem. When I saw that problem in the contest, I also had no idea how to solve it. But after learning this trick, it seemed pretty easy to me. I hope you also don't find this problem hard anymore after reading this blog.
Also I give online classes, $$${\$25}$$$ per hour for one on one lessons, $$${\$8}$$$ per hour for lessons in groups of 3, free trial lesson. Contact me on Codeforces if you are interested or for more info.











Distance in $$$ST$$$ coordinates has a formal name — Chebyshev distance
I think you might have over complicated your first solution (The one without the trick). Manhattan distance is very symmetric, you can take advantage of it by mapping all cases to a single case.
Assume that $$$(x_1,y_1)$$$ is the bottom-most and leftmost point of a triangle (the other two points lie in its top-right quadrant). Obs: if a triangle has no such point, the test case can be mirrored (on one or both axis) to make it so.
Given that assumption, it should be clear the other two points must be on the line $$$x+y = x_1+y_1+d$$$ and satisfy the constraints $$$x\geq x_1$$$ and $$$y\geq y_1$$$.
After these observations, the solution goes as follows:
Iterate over all points from right to left. For a given point $$$(x,y)$$$ check on diagonal $$$x+y+d$$$ if there is a pair of already-seen points with distance $$$d$$$ and where the lower y-coordinate is greater than or equal to $$$y$$$.
You can do this by maintaining a
map<int,map<int,pair<int,int>>>that mapsdiagonal -> lower y-coordinate -> pair of indices. Specifically, after looking at a point $$$(x,y)$$$ check if there exists a point $$$(x+d/2,y-d/2)$$$ and, if so, add that pair to the data structure.Run this algorithm four times, once for each combination of mirroring operations.
Implementation
I wrote this a few minutes ago. During the contest I had a similar idea but my code was a lot uglier because I special-cased some unnecessary stuff.
Wow, looks a lot easier than mine, really cool).
I struggled with the diagonals and decided to split the into 2 cases, and it made everything look pretty ugly. I think from my implementations I like the one in the algebra section the most
As a tester, I was told that they give out free contribution for testing :) As a Spanish teacher who was forced to learn about Manhattan distances by the author, lloré al final :(
Instructions unclear, I am now permanently stuck on Broadway.
This is my favorite trick. I'm so happy to see someone wrote a blog about it :)
Here are some practice problems:
Lazy Cow
Apple Catching
Isnt it like $$$s = y + x$$$ , $$$t = y - x$$$ , in the blog you say $$$s = y + x$$$ , $$$t = -y + x$$$ which is a bit confusing to think of since when we do it that way we rotate it by $$$45$$$ degrees then flip it (points on the $$$x$$$ axis go to axis $$$s$$$ and points on the $$$y$$$ axis go to axis $$$t$$$).
If we do it $$$s = y + x$$$ , $$$t + y - x$$$ , axis $$$x$$$ becomes axis $$$t$$$ , and $$$y$$$ becomes axis $$$s$$$ which is actually rotating it by $$$45$$$ degrees.
please correct me if I am wrong.
Wandoka in step 4 of algebraic solution t1+t2=2*t3 is also possible isn't?