Hello, %username%
Recently, I made a chess engine in pure C++, which I named Mufasa, making wordplay on the phrase "move faster". Here is the corresponding GitHub page (make sure you star it if you find it resourceful!)
Because of that I wanted to share what interesting things that relate to competitive programming you might come across while developing a similar project.
1. Branchless programming and bitmasks
There is a beauty in a fact that each cell on the chessboard can be represented by a long integer as there are exactly 64 cells. This concept is called bitboard and is used by almost every fast chess engine. Why? Because it allows for less branching during move generation. For example, consider we want a mask of left pawn attacks. A naive approach would be to loop through each and every pawn and get the corresponding left square. But with bitmasks we can write something like ((~a_file & wpawns) << 7), where a_file is a bitmask for the a file on the board and wpawns is a bitmask for white pawns. Here we negate a_file from wpawns because shifting a pawn on "a" file to the upper left cell may result in wrapping and we would suddenly attack cell on "h" file, which is not correct but fun to play with. For canonical initial position in chess wpawns would hold a value of 0b1111111100000000. Notice that the least significant first bit corresponds to cell a1, the second to a2, and so on. Thus we make use of less processor instructions.
2. Built-in functions
But what if we specifically wanted to loop through each piece on the board with bitboard? For that purpose we somehow need to create and loop a function that takes the least significant bit (LSB) in the bitmask and pops it. In the best case, you may find that for that purpose CPU manufacturers already created "count trailing zeros" instruction, which we can access in C++ with a built-in function __builtin_ctzll. We simply execute the function and get zero indexed position of our LSB in the long long integer. To pop that LSB we can do bitwise magic like this bits &= (bits-1). You can try to understand how that works for yourself!
But that is the best case! What if our CPU does not support such functions? Then one of the option is through the use of de Bruijn sequence. De Bruijn's sequence is just a cyclical string containing all permutations of order n of alphabet of size k. One example could be a de Bruijn sequence for binary alphabet B(2, 2), namely 0011. Notice that the sequence loops around to cover up for combination 10. How do we use that?
Firstly, we isolate the LSB through b &= (b-1). Now we have sixty four variations of our long long integer. Now comes the genius part. Notice that each lone bit represents the number that is the power of two and multiplying our isolated LSB by some number is exactly shifting that number to the right n times, where n is the position of our active bit, counting from one! We can use that information on our de Bruijn sequence of length 64 (i.e. B(2, 6)) because each part of that sequence is unique! That creates perfect hash function mapping each LSB to corresponding combination of bits! Now we just need a hash table a.k.a array which maps each combination to the index that creates it. You can read more about that technique here.
3. Graphs and DFS
Classical and time honored way to evaluate a position in general games is through minimax algorithm. To use it one must build a game tree, where each node is a position and each vertex is a move. To build it, we firstly traverse each node depth first and secondly evaluate the position at the leaf nodes, using positive score to indicate if position is better for white and negative if for black. Then in each parent node we choose the maximum score among all children nodes if the node holds position for maximizer alas white to play, or minimum score if it holds position for minimizer alas black to play.
4. Hashing
One of the disadvantages of building and evaluating such game tree is cycles. Consider this position, which can be reached through two different variations of the Sicilian:
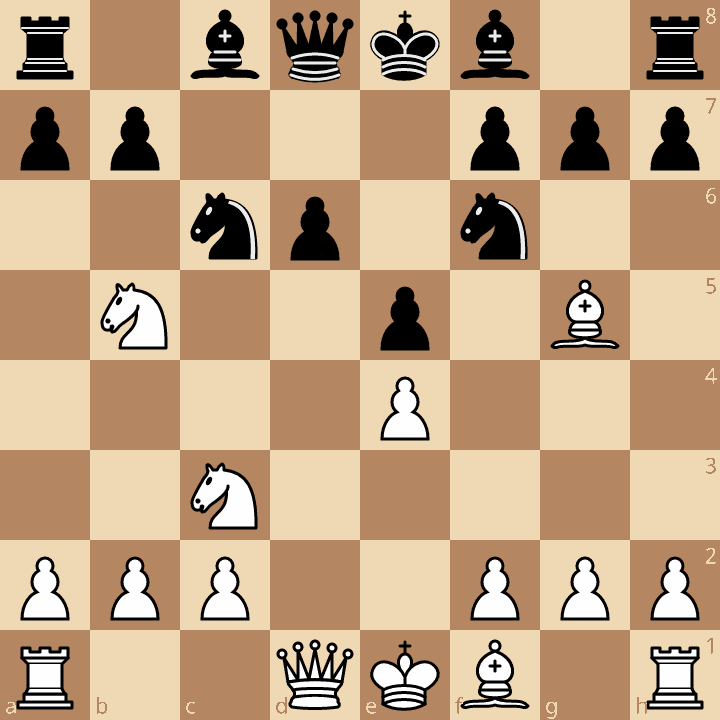
- e4 c5 2. Nf3 d6 3. d4 cxd 4. Nxd4 Nf6 5. Nc3 Nc6 6. Bg5 e5 7. Ndb5
- e4 c5 2. Nc3 e6 3. Nf3 Nc6 4. d4 cxd 5. Nxd4 Nf6 6. Ndb5 d6 7. Bf4 e5 8. Bg5
So how we can transform our tree to get a directed acyclic graph (DAG)? One of the answers is hashing: we mark which positions we already visited at what depth and thus do less work if we can. Of course, ones familiar with chess would think of FEN strings but they are slow to generate. Instead we can use zobrist hashing! What we do is associate a unique hash to each piece on a certain square and each game state (i.e. black to move, castling for black kingside, castling for white queenside, etc.), and then XOR hashes belonging to variables that describe our position (i.e black rook on e8, white to move, etc.)
Another use of hashing is to generate magic bitboards for efficient sliding piece move generation (queens, rooks, bishops.) But describing how that works is pretty mouthful and there is already a nice blog about that by analog-hors.
Fin
What has been shown is not all the chess programming but it concludes the end of this article! If you want the second part please let me know! Hope you have a great day!











Representing board with pieces as a bunch of bitmasks is brilliant!
It is nice but gets in a way when you want to check what piece resides at a certain square. For that purpose chess engines simultaneously manage a mailbox array of size 64 for quick piece access. You can check my repo for more information.