idea & solution: xcyle
Consider the case with $$$n=m=k$$$.
Generalize the solution for all $$$n,m,k$$$.
It can be shown that for any $$$k\times k$$$ subgrid, the colors we use must be pairwise distinct. Thus, we have an lower bound of $$$\min(n,k)\cdot\min(m,k)$$$. We can show that this lower bound is indeed achievable by coloring the upper-left $$$\min(n,k)\cdot\min(m,k)$$$ subgrid with distinct colors, and copy-pasting it to fill the rest of the grid.
Time complexity: $$$O(1)$$$.
#include <bits/stdc++.h>
using namespace std;
int t, n, m, k;
int main() {
scanf("%d", &t);
while (t--) {
scanf("%d%d%d", &n, &m, &k);
printf("%d\n", min(n, k)*min(m, k));
}
return 0;
}
idea & solution: xcyle
Find some conditions that Bob need to win.
A general idea is that it is very difficult for Bob to win. We make some observations regarding the case where Bob wins. It is intuitive to see that for any subarray $$$[A_l,A_{l+1},\cdots,A_r]$$$, the elements' positions in $$$B$$$ must also form an interval. If $$$A[l:r]$$$ does not form an interval in $$$B$$$, Alice can simply remove elements until only $$$A[l:r]$$$ is left, no matter how Bob plays, there must now be an element in $$$A$$$ but not in $$$B$$$ because of our previous condition. Alice can then remove everything other than this element to win.
From here, it is easy to prove by induction that for Bob to win, either $$$A=B$$$ or $$$A=\textrm{rev}(B)$$$.
Time complexity: $$$O(n)$$$.
#include <bits/stdc++.h>
#define ll long long
#define lc(x) ((x) << 1)
#define rc(x) ((x) << 1 | 1)
#define ru(i, l, r) for (int i = (l); i <= (r); i++)
#define rd(i, r, l) for (int i = (r); i >= (l); i--)
#define mid ((l + r) >> 1)
#define pii pair<int, int>
#define mp make_pair
#define fi first
#define se second
#define sz(s) (int)s.size()
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
using namespace __gnu_pbds;
#define ordered_set tree<int, null_type, less<int>, rb_tree_tag, tree_order_statistics_node_update>
using namespace std;
mt19937 Rand(chrono::steady_clock::now().time_since_epoch().count());
int read() {
int x = 0, w = 0;
char ch = getchar();
while (!isdigit(ch))
w |= ch == '-', ch = getchar();
while (isdigit(ch))
x = x * 10 + ch - '0', ch = getchar();
return w ? -x : x;
}
int main() {
int T = read();
while (T--) {
int n = read();
vector<int> a, b;
ru(i, 1, n) a.push_back(read());
ru(i, 1, n) b.push_back(read());
if (a == b) {
printf("Bob\n");
continue;
}
reverse(a.begin(), a.end());
if (a == b) {
printf("Bob\n");
continue;
}
printf("Alice\n");
}
return 0;
}
The problem can't be that hard, find some simple strategy.
We consider a simple strategy: walk towards the goal in a straight line.
If some circle reaches the goal first, it is obvious that we have no chance of succeeding, no matter what path we take.
Otherwise, it can be proven that we will not pass any circles on our way to the goal.
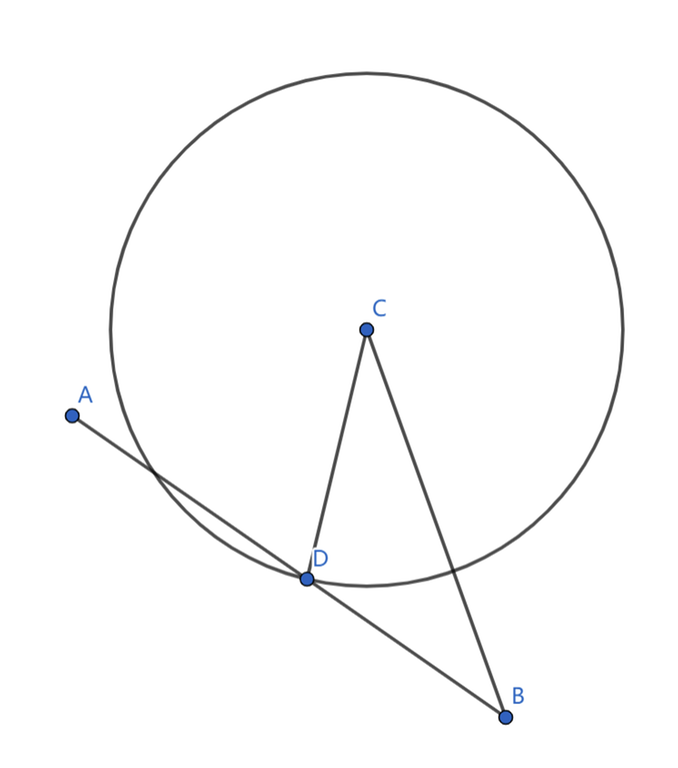
Suppose we start at $$$A$$$, our goal is $$$B$$$, and we got intercepted by some circle $$$C$$$ at the point $$$D$$$. It follows that $$$CD=AD$$$. According to the triangle inequality, $$$CD>CB-DB$$$ should hold. Thus, we have $$$CB-DB\le AD$$$, which means $$$CB\le AB$$$, proof by contradiction.
Time complexity: $$$O(n)$$$.
#include <bits/stdc++.h>
#define ll long long
using namespace std;
int t, n, x[100011], y[100011], xs, ys, xt, yt;
ll dis(int x1, int y1, int x2, int y2) {
return 1ll * (x2 - x1) * (x2 - x1) + 1ll * (y2 - y1) * (y2 - y1);
}
int main() {
scanf("%d", &t);
while (t--) {
scanf("%d", &n);
for (int i = 1; i <= n; ++i)
scanf("%d%d", x + i, y + i);
scanf("%d%d%d%d", &xs, &ys, &xt, &yt);
bool ok = 1;
for (int i = 1; i <= n; ++i) {
if (dis(xt, yt, x[i], y[i]) <= dis(xt, yt, xs, ys)) {
ok = 0;
break;
}
}
printf(ok ? "YES\n" : "NO\n");
}
fclose(stdin);
fclose(stdout);
return 0;
}
2002D1 — DFS Checker (Easy Version) and 2002D2 — DFS Checker (Hard Version)
idea & solution: xcyle
Try to find some easy checks that can be maintained.
The problem revolves around finding a check for dfs orders that's easy to maintain. We have discovered several such checks, a few checks and their proofs are described below, any one of these checks suffices to tell whether a dfs order is valid.
For every $$$u$$$, all of its children $$$v$$$ satisfies $$$[pos_v,pos_v+siz_v-1]\subseteq[pos_u,pos_u+siz_u-1]$$$. We can maintain this check by keeping track of the number of $$$u$$$ which violates this condition, and check for each $$$u$$$ using sets, when checking, we need only check the child with the minimum $$$pos_v$$$ and maximum $$$pos_v+siz_v-1$$$.
Proof: We prove by induction. When $$$u$$$'s children only consists of leaves, it is easy to see that this check ensures $$$[pos_u,pos_u+siz_u-1]$$$ is a valid dfs order of the subtree of $$$u$$$. Then, we can merge the subtree of $$$u$$$ into a large node with size $$$siz_u$$$, and continue the analysis above.
Check 2: First we check $$$p_1=1$$$. Then, for each pair of adjacent elements $$$p_i,p_{i+1}$$$, $$$fa(p_{i+1})$$$ must be an ancestor of $$$p_i$$$, where $$$fa(u)$$$ denotes the father of node $$$u$$$. We can maintain this check by keeping track of the number of $$$u$$$ which violates this condition, and check for each $$$i$$$ by checking whether $$$p_i$$$ is in the subtree of $$$fa(p_{i+1})$$$.
Proof: For any subtree $$$u$$$, we take any $$$p_i,p_{i+1}$$$ such that $$$p_i$$$ does not belong in subtree $$$u$$$, but $$$p_{i+1}$$$ does. It follows that $$$p_{i+1}=u$$$, since only the subtree of $$$fa(u)$$$ has nodes that does not belong in subtree $$$u$$$. From this, we can gather that each subtree will be entered at most once (and form a continuous interval), and that the first visited node will be $$$u$$$, which is sufficient to say that $$$p$$$ is a dfs order.
Time complexity: $$$O((n+q)\log n)/O(n+q)$$$.
#include <bits/stdc++.h>
#define ll long long
#define lc(x) ((x) << 1)
#define rc(x) ((x) << 1 | 1)
#define ru(i, l, r) for (int i = (l); i <= (r); i++)
#define rd(i, r, l) for (int i = (r); i >= (l); i--)
#define mid ((l + r) >> 1)
#define pii pair<int, int>
#define mp make_pair
#define fi first
#define se second
#define sz(s) (int)s.size()
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
using namespace __gnu_pbds;
#define ordered_set tree<int, null_type, less<int>, rb_tree_tag, tree_order_statistics_node_update>
using namespace std;
#define maxn 500005
mt19937 Rand(chrono::steady_clock::now().time_since_epoch().count());
int read() {
int x = 0, w = 0; char ch = getchar();
while(!isdigit(ch)) w |= ch == '-', ch = getchar();
while(isdigit(ch)) x = x * 10 + ch - '0', ch = getchar();
return w ? -x : x;
}
int n, Q, fa[maxn], p[maxn], q[maxn], siz[maxn];
set<int> son[maxn];
int chk(int x) {
return son[x].empty() ? 1 : (q[x] < *son[x].begin() && *--son[x].end() + siz[p[*--son[x].end()]] <= q[x] + siz[x]);
}
void solve() {
n = read(), Q = read();
ru(i, 1, n) siz[i] = 1, son[i].clear();
ru(i, 2, n) fa[i] = read();
rd(i, n, 2) siz[fa[i]] += siz[i];
ru(i, 1, n) son[fa[p[i] = read()]].insert(i), q[p[i]] = i;
int cnt = 0;
ru(i, 1, n) cnt += chk(i);
while(Q--) {
int i = read(), j = read(), x = p[i], y = p[j];
set<int> s; s.insert(x), s.insert(y), s.insert(fa[x]), s.insert(fa[y]);
for (auto x: s) if(x) cnt -= chk(x);
son[fa[x]].erase(i), son[fa[y]].erase(j);
swap(p[i], p[j]), swap(q[x], q[y]);
son[fa[x]].insert(j), son[fa[y]].insert(i);
for (auto x: s) if(x) cnt += chk(x);
puts(cnt == n ? "YES" : "NO");
}
}
int main() {
int T = read();
while(T--) solve();
return 0;
}
#include <bits/stdc++.h>
using namespace std;
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define int long long
void dbg_out() { cerr << endl; }
template <typename H, typename... T>
void dbg_out(H h, T... t) { cerr << ' ' << h; dbg_out(t...); }
#define dbg(...) { cerr << #__VA_ARGS__ << ':'; dbg_out(__VA_ARGS__); }
using ll = long long;
mt19937_64 rng(chrono::steady_clock::now().time_since_epoch().count());
const int MAXN = 3e5 + 5;
const int MOD = 1e9+7; //998244353;
const int INF = 0x3f3f3f3f;
const ll INF64 = ll(4e18) + 5;
vector<int> g[MAXN];
int tin[MAXN];
int tout[MAXN];
int id[MAXN];
int par[MAXN];
int T = 0;
void dfs(int u, int p){
id[u] = tin[u] = tout[u] = T++;
for(auto v : g[u]) if(v != p){
dfs(v,u);
par[v] = u;
tout[u] = tout[v];
}
}
void solve(){
int n,q;
cin >> n >> q;
vector<int> p(n+1);
for(int i = 0; i <= n; i++) g[i].clear();
T = 0;
for(int i = 2; i <= n; i++){
int pi;
cin >> pi;
g[pi].push_back(i);
}
for(int i = 1; i <= n; i++){
cin >> p[i];
}
dfs(1,1);
int cnt = 0;
auto ok = [&](int i){
if(p[i] == 1){
if(i == 1) return 1;
return 0;
}
int ant = p[i-1];
if(par[p[i]] == ant) return 1;
if(tin[ant] != tout[ant]) return 0;
int pa = par[p[i]];
if(tin[ant] < tin[pa] || tin[ant] > tout[pa]) return 0;
return 1;
};
for(int i = 1; i <= n; i++){
cnt += ok(i);
}
for(int qw = 0; qw < q; qw++){
int x,y;
cin >> x >> y;
set<int> in;
in.insert(x);
in.insert(y);
if(x-1 >= 1) in.insert(x-1);
if(x+1 <= n) in.insert(x+1);
if(y-1 >= 1) in.insert(y-1);
if(y+1 <= n) in.insert(y+1);
for(auto v : in){
cnt -= ok(v);
}
swap(p[x],p[y]);
for(auto v : in){
cnt += ok(v);
}
cout << (cnt == n ? "YES": "NO") << '\n';
}
}
signed main(){
ios::sync_with_stdio(false); cin.tie(NULL);
int t = 1;
cin >> t;
while(t--){
solve();
}
return 0;
}
Consider an incremental solution.
Use stacks.
The problems asks for the answer for every prefix, which hints at an incremental solution.
To add a new pair to the current prefix, we need to somehow process the new block merging with old ones. Thus, we should use some structure to store the information on the last block over time.
Namely, we use a stack to keep track of all blocks that became the last. For each block, we keep two values: its color $$$c$$$ and its lifetime $$$l$$$ (the times it takes for the block to disappear).
When inserting a new block, we pop all blocks that would be shadowed by the current one (i.e. with lifetime shorter than the current block), and merging blocks with the same $$$a$$$. When merging two blocks with length $$$x$$$ and $$$z$$$, and the maximum lifetime of blocks between them is $$$y$$$, $$$y\le\min(x,z)$$$ should hold, and the new block will have lifetime $$$x+z-y$$$.
For more details, please refer to the solution code.
There also exists $$$O(n\log n)$$$ solutions using ordered sets or heaps.
Time complexity: $$$O(n)$$$.
#include <bits/stdc++.h>
#define N 1000011
#define ll long long
#define pii pair<ll,int>
#define s1 first
#define s2 second
using namespace std;
int t, n, b[N];
ll a[N];
pii s[N];
int sn;
int main() {
scanf("%d", &t);
while (t--) {
scanf("%d", &n);
for (int i = 1; i <= n; ++i)
scanf("%lld%d", a + i, b + i);
sn = 0;
ll x = 0;
for (int i = 1; i <= n; ++i) {
ll mx = 0;
while (sn) {
if (s[sn].s2 == b[i])
a[i] += s[sn--].s1 - mx;
else if (s[sn].s1 <= a[i])
mx = max(mx, s[sn--].s1);
else
break;
}
++sn;
s[sn] = pii(a[i], b[i]);
x = max(x, s[sn].s1);
printf("%lld ", x);
}
putchar(10);
}
return 0;
}
#include <bits/stdc++.h>
#define ll long long
#define N 3000011
#define pii pair<ll,int>
#define s1 first
#define s2 second
using namespace std;
int t, n, prv[N], nxt[N], b[N];
ll a[N];
priority_queue<pair<ll, int>> pq, del;
ll sum = 0, ans[N];
int main() {
scanf("%d", &t);
while (t--) {
scanf("%d", &n);
for (int i = 1; i <= n; ++i)
scanf("%lld%d", a + i, b + i);
while (!pq.empty())
pq.pop();
while (!del.empty())
del.pop();
nxt[0] = 1;
prv[n + 1] = n;
for (int i = 1; i <= n; ++i)
pq.push({-a[i], i}), prv[i] = i - 1, nxt[i] = i + 1;
ll tim = 0;
int lst = 1;
for (int _ = 1; _ <= n; ++_) {
while (!del.empty() && pq.top() == del.top())
pq.pop(), del.pop();
pii p = pq.top();
pq.pop();
int id = p.s2;
tim = -p.s1;
if (nxt[id] <= n && b[id] == b[nxt[id]]) {
a[nxt[id]] += tim;
pq.push({-a[nxt[id]], nxt[id]});
}
if (prv[id] && nxt[id] <= n && b[prv[id]] == b[nxt[id]]) {
del.push({-a[nxt[id]], nxt[id]});
a[nxt[id]] -= tim;
}
prv[nxt[id]] = prv[id];
nxt[prv[id]] = nxt[id];
while (lst < nxt[0])
ans[lst++] = tim;
}
for (int i = 1; i <= n; ++i)
printf("%lld ", ans[i]);
putchar(10);
}
return 0;
}
2002F1 — Court Blue (Easy Version)
Primes are powerful.
Prime gaps are small.
We view the problem as a walk on grid, starting at $$$(1,1)$$$. WLOG, we suppose $$$l>f$$$, thus only cells $$$(a,b)$$$ where $$$a<b$$$ would be considered.
Notice that when $$$n$$$ is large enough, the largest prime $$$p\le n$$$ satisfies $$$2p>n$$$. As such, all cells $$$(p,i)$$$ where $$$i<p$$$ will be unblocked and reachable.
However, we've only bounded one side of the final result. We take this a step further, let $$$q$$$ be the second-largest prime $$$q\le n$$$. By the same logic, we assume that $$$2q>n$$$. As such, all cells $$$(i,q)$$$, where $$$p\le i\le n$$$ will be unblocked and reachable.
Thus, we have constructed an area where the optimal solution must be, with its dimensions bounded by $$$n-p$$$ and $$$n-q$$$. We just need to run any brute force solution (dfs with memorization or dp) on this area to find the result.
If we assume the asymptotic of prime gap is $$$O(P(n))$$$, this yields a $$$O(n\cdot P(n)^2\cdot\log P(n))$$$ solution, where the $$$\log\log n$$$ is from taking the gcd of two numbers which differ by $$$O(P(n))$$$. This can also be optimized to $$$O(n\cdot P(n)^2)$$$ by preprocessing gcd.
We added the constraints that $$$n$$$'s are pairwise distinct to avoid forcing participants to write memorizations. In fact, under the constraints of the problem, the maximum area is $$$39201$$$, and the sum of the $$$10^3$$$ largest areas is $$$2.36\times10^7$$$.
Time complexity: $$$O(P(n)^2\log P(n))/O(P(n)^2)$$$
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 2e7 + 5;
bool ntp[N];
int di[405][405];
bool bad[405][405];
int pos[N], g = 0, m = 3;
int prime[2000005], cnt = 0;
void sieve(int n) {
int i, j;
for (i = 2; i <= n; i++) {
if (!ntp[i])
prime[++cnt] = i;
for (j = 1; j <= cnt && i * prime[j] <= n; j++) {
ntp[i * prime[j]] = 1;
if (!(i % prime[j]))
break;
}
}
}
int gcd(int x, int y) {
if (!x)
return y;
if (x <= g && y <= g)
return di[x][y];
return gcd(y % x, x);
}
int main() {
sieve(2e7);
int i, j = 1, T, n, a, b, c, u, v;
ll ans;
for (i = 3; i <= 2e7; i++) {
while (j < cnt - 1 && prime[j + 2] <= i)
j++;
g = max(g, i - prime[j] + 1);
if (prime[j] * 2 <= i)
m = i;
pos[i] = j;
}
for (i = 0; i <= g; i++)
for (j = 0; j <= g; j++)
if (!i)
di[i][j] = j;
else
di[i][j] = di[j % i][i];
scanf("%d", &T);
while (T--) {
scanf("%*d%d%d%d", &n, &a, &b);
if (n <= m)
u = v = 1;
else {
u = prime[pos[n] + 1];
v = prime[pos[n]];
}
ans = 0;
for (i = u; i <= n; i++)
for (j = v; j <= i; j++) {
bad[i - u + 1][j - v + 1] = (gcd(i, j) > 1 || (bad[i - u][j - v + 1] && bad[i - u + 1][j - v]));
if (!bad[i - u + 1][j - v + 1])
ans = max(ans, max((ll)a * i + (ll)b * j, (ll)a * j + (ll)b * i));
}
printf("%lld\n", ans);
}
return 0;
}
2002F2 — Court Blue (Hard Version)
Try generalizing the solution of F1.
Write anything and pray that it will pass because of number theory magic.
We generalize the solution in F1. Let $$$p$$$ be the largest prime $$$\le m$$$ and $$$q$$$ be the largest prime $$$\le\min(n,p-1)$$$. The problem is that there might be $$$\gcd(q,i)\neq1$$$ for some $$$p+1\le i\le m$$$, thus invalidating our previous analysis.
To solve this, we simply choose $$$q$$$ to be the largest integer such that $$$q\le n$$$ and $$$\gcd(q,i)=1$$$ for all $$$p+1\le i\le m$$$. An asymptotic analysis of this solution is as follows:
As the length of $$$[p+1,m]$$$ is $$$O(P(m))$$$, and each of these integers have at most $$$O(\log_nm)$$$ prime divisors of $$$O(m)$$$ magnitude, which means that if we only restrict $$$q$$$ to primes, we will have to skip at most $$$O(P(n)\log_nm)$$$ primes to find the largest $$$q$$$. As the density of primes is $$$O(\frac1{P(n)})$$$, the asymptotic of $$$n-q$$$ will be $$$O(P(m)\log_nm\cdot P(n))=O(P(m)^2)$$$, our actual $$$q$$$ (which is not restricted to primes) will not be worse than this. Thus, our total area will be $$$O(P(m)^3)$$$, times the gcd complexity gives us an $$$O(P(m)^3\log m)$$$ solution. However, the actual area is much lower than this.
Under the constraints of the problem, when forcing $$$p,q$$$ to take primes, the maximum area is $$$39960$$$, and the sum of the $$$10^3$$$ largest areas is $$$3.44\times10^7$$$. The actual solution will not be worse than this.
Because we only need to check whether $$$\gcd(x,y)=1$$$, the complexity can actually be optimized to $$$O(P(m)^3)$$$ with some sieves. Namely, iterating over prime divisors $$$d$$$ of $$$[p,m]$$$ and $$$[q,n]$$$ and marking all cells which has $$$d$$$ as its common divisor.
This solution is by far from optimal. We invite you to continue optimizing your solutions and try to minimize the number of cells visited in each query :)
Time complexity: $$$O(P(m)^3\log m)$$$
Keep $$$p$$$ the same, set $$$q$$$ to $$$p-L$$$ and only keep reachable cells in $$$[p,n]\times [q,m]$$$. $$$L$$$ is some constant ($$$100$$$ should work).
We found this solution during testing, tried, and failed to hack it.
Keep $$$p$$$ the same, do dfs from each cell $$$(n,p),(n-1,p),\cdots$$$, prioritizing increasing $$$W_L$$$ over increasing $$$W_F$$$, and stop the process the first time you reach any cell $$$(x,m)$$$, take the maximum of all cells visited.
This should not be worse than the intended solution, and actually runs quite fast.
Simply take all cells in $$$[n-L,n]\times [m-L,m]$$$ and mark everything outside as reachable. $$$L=50$$$ works.
We found this solution the day before the round, we don't know how to hack it either.
UPD: $$$L=50$$$ was hacked. Hats off to the hacker.
Do dfs with pruning. Run dfs starting at $$$(n,m)$$$, return when the cell is $$$(p,i)$$$ (i.e. obviously reachable because of primes), or when the value of the cell is smaller than the current answer. Add some memorization and it passes.
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 2e7 + 5;
bool ntp[N];
bool bad[405][405];
int pos[N];
int prime[2000005], mn[N], cnt;
void sieve(int n) {
int i, j;
for (i = 2; i <= n; i++) {
if (!ntp[i])
prime[++cnt] = i, mn[i] = i;
for (j = 1; j <= cnt && i * prime[j] <= n; j++) {
mn[i * prime[j]] = prime[j];
ntp[i * prime[j]] = 1;
if (!(i % prime[j]))
break;
}
}
}
int gcd(int x, int y) {
return x ? gcd(y % x, x) : y;
}
bool no(int l, int r, int k) {
while (k > 1) {
int x = mn[k];
while (k % x == 0)
k /= x;
if (((l + x - 1) / x) * x <= r)
return 0;
}
return 1;
}
int main() {
sieve(20000000);
int i, j = 0, T, n, m, a, b, u, v, g = 0, S = 0, px, py, qwq = 0;
ll ans;
prime[0] = 1;
for (i = 2; i <= 20000000; i++) {
while (j < cnt && prime[j + 1] <= i)
j++;
pos[i] = j;
}
scanf("%d", &T);
while (T--) {
scanf("%d%d%d%d", &n, &m, &a, &b);
if (n < m) {
swap(n, m);
swap(a, b);
}
u = prime[pos[n]];
v = m;
while (v && !no(u, n, v))
v--;
ans = 0;
px = py = 0;
for (i = u; i <= n; i++)
for (j = v; j <= m && j <= i; j++) {
bad[i - u + 1][j - v + 1] = ((bad[i - u][j - v + 1] && bad[i - u + 1][j - v]) || gcd(i, j) > 1);
if (!bad[i - u + 1][j - v + 1]) {
ans = max(ans, (ll)a * i + (ll)b * j);
if ((ll)a * i + (ll)b * j == ans) {
px = i;
py = j;
}
if (i <= m)
ans = max(ans, (ll)a * j + (ll)b * i);
}
}
qwq = max(qwq, (n - px) + (m - py));
printf("%lld\n", ans);
}
return 0;
}
#include <bits/stdc++.h>
#define ll long long
#define N 20000011
using namespace std;
int t, n, m, a, b;
bool is[N];
int pr[N / 10];
int gcd(int a, int b) {
while (b)
a %= b, swap(a, b);
return a;
}
ll ans = 0;
bool vis[1011][1011];
pair<int, int> vv[200011];
int vn, c;
bool flg = 0;
inline ll V(int i, int j) {
return i <= n ? 1ll * max(i, j) * max(a, b) + 1ll * min(i, j) * min(a, b) : 1ll * i * b + 1ll * j * a;
}
void dfs(int i, int j) {
++c;
bool mk = gcd(i, j) == 1;
if (!mk)
return;
ans = max(ans, V(i, j));
vis[m - i][n - j] = 1;
vv[++vn] = {i, j};
if (j < n && !vis[m - i][n - j - 1])
dfs(i, j + 1);
if (i == m || flg) {
flg = 1;
return;
}
if (i < m && !vis[m - i - 1][n - j])
dfs(i + 1, j);
}
int main() {
is[0] = is[1] = 1;
for (int i = 2; i < N; ++i) {
if (!is[i])
pr[++pr[0]] = i;
for (int j = 1; j <= pr[0] && i * pr[j] < N; ++j) {
is[i * pr[j]] = 1;
if (i % pr[j] == 0)
break;
}
}
scanf("%d", &t);
while (t--) {
scanf("%d%d%d%d", &n, &m, &a, &b);
int p;
if (m <= 10)
p = 1;
else {
p = m;
while (is[p])
--p;
}
vn = 0;
ans = 0;
flg = 0;
c = 0;
for (int i = min(n, p - (p > 1));; --i) {
assert(i > 0);
ans = max(ans, V(p, i));
if (p < m)
dfs(p + 1, i);
else
break;
if (flg)
break;
}
for (int i = 1; i <= vn; ++i)
vis[m - vv[i].first][n - vv[i].second] = 0;
printf("%lld\n", ans);
}
return 0;
}
idea & solution: xcyle
We apologize for unintended solutions passing, and intended solutions failing with large constants. Brute force runs very fast on $$$n=18$$$, which forced us to increase constraints.
Meet in the middle with a twist.
Union of sets is hard. Disjoint union of sets is easy.
The problem hints strongly at meet in the middle, at each side, there will be $$$O(2^n)$$$ paths. The twist is on merging: we are given two sequence of sets $$$S_1,S_2,\cdots$$$ and $$$T_1,T_2,\cdots$$$, we have to find the maximum $$$\textrm{MEX}(S_i\cup T_j)$$$.
If we enumerate over the maximum MEX $$$P$$$, we only need to check whether there exists two sets such that $$$\{ 0,1,\cdots,P-1\} \subseteq S_i\cup T_j$$$.
Instead of meeting at $$$n$$$, we perform meet in the middle at the partition of $$$Bn$$$ and $$$(2-B)n$$$. For each $$$S_i$$$, we put all its subsets $$$S^\prime_i$$$ into a hashmap. When checking MEX $$$P$$$, we iterate over all $$$T_j$$$, and check whether $$$\{ 0,1,\cdots,P-1\} -T_j$$$ is in the hashmap. This gives us a $$$O((2^{2Bn}+2^{(2-B)n})\cdot n)$$$ solution, which is optimal at $$$B=\frac23$$$, where the complexity is $$$O(2^{\frac43}\cdot n)$$$.
We can substitute enumerating $$$P$$$ with binary search, yielding $$$O(2^{\frac43n}\cdot\log n)$$$, or checking whether $$$P$$$ can be increased each time, yielding $$$O(2^{\frac43n})$$$.
Instead of hashmaps, you can also insert all $$$S$$$ and $$$T$$$'s into a trie, and run a brute force dfs to search for MEX $$$P$$$. It can be proven that the complexity is also $$$O(2^{\frac43n}\cdot n)$$$.
The intended solution is $$$O(2^{\frac43 n})$$$, however solutions that have slightly higher complexity can pass with good optimizations.
Time complexity: $$$O(2^{\frac43n})$$$.
#include <bits/stdc++.h>
#define ll long long
using namespace std;
int D[111][111], R[111][111], n;
const int P = 30000019;
struct custom_hash {
static uint64_t splitmix64(uint64_t x) {
// http://xorshift.di.unimi.it/splitmix64.c
x += 0x9e3779b97f4a7c15;
x = (x ^ (x >> 30)) * 0xbf58476d1ce4e5b9;
x = (x ^ (x >> 27)) * 0x94d049bb133111eb;
return x ^ (x >> 31);
}
size_t operator()(uint64_t x) const {
static const uint64_t FIXED_RANDOM = chrono::steady_clock::now().time_since_epoch().count();
return splitmix64(x + FIXED_RANDOM);
}
} HH;
int sta[P], top;
struct uset {
struct edge {
pair<int, ll> v;
int next;
edge() {} edge(pair<int, ll> _v, int _next) {
v = _v;
next = _next;
}
} e[20000011];
int head[P], sz;
uset() {
memset(head, -1, sizeof(head));
sz = 0;
}
void insert(pair<int, ll> x) {
int u = HH(x.second * n + x.first) % P;
sta[++top] = u;
for (int i = head[u]; ~i; i = e[i].next)
if (e[i].v == x)
return;
e[++sz] = edge(x, head[u]);
head[u] = sz;
}
bool find(pair<int, ll> x) {
int u = HH(x.second * n + x.first) % P;
for (int i = head[u]; ~i; i = e[i].next)
if (e[i].v == x)
return 1;
return 0;
}
} st;
int B;
void dfs1(int x, int y, ll S, int tp) {
if (x + y == B) {
st.insert({x, S});
return;
}
if (y < n) {
dfs1(x, y + 1, S, 0);
dfs1(x, y + 1, S | 1ll << R[x][y], -1);
}
if (x < n) {
if (tp != 0)
dfs1(x + 1, y, S, 1);
dfs1(x + 1, y, S | 1ll << D[x][y], -1);
}
}
int ans = 0;
void dfs2(int x, int y, ll S) {
if (x + y == B) {
int res = 0;
while (ans <= 2 * n - 2) {
if (st.find({x, (~S) & (1ll << (ans + 1)) - 1}))
ans++;
else
break;
}
return;
}
if (x > 1)
dfs2(x - 1, y, S | 1ll << D[x - 1][y]);
if (y > 1)
dfs2(x, y - 1, S | 1ll << R[x][y - 1]);
}
void solve() {
while (top)
st.head[sta[top--]] = -1;
st.sz = 0;
ans = 0;
scanf("%d", &n);
for (int i = 1; i < n; ++i)
for (int j = 1; j <= n; ++j)
scanf("%d", D[i] + j);
for (int i = 1; i <= n; ++i)
for (int j = 1; j < n; ++j)
scanf("%d", R[i] + j);
B = 2 * n / 3 + 2;
dfs1(1, 1, 0, -1);
dfs2(n, n, 0);
printf("%d\n", ans);
}
int main() {
int T;
scanf("%d", &T);
while (T--)
solve();
return 0;
}
#include <bits/stdc++.h>
using namespace std;
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define int long long
void dbg_out() {
cerr << endl;
}
template <typename H, typename... T>
void dbg_out(H h, T... t) {
cerr << ' ' << h;
dbg_out(t...);
}
#define dbg(...) { cerr << #__VA_ARGS__ << ':'; dbg_out(__VA_ARGS__); }
using ll = long long;
mt19937_64 rng(chrono::steady_clock::now().time_since_epoch().count());
const int MAXN = 3e7 + 5;
const int MOD = 1e9 + 7; //998244353;
const int INF = 0x3f3f3f3f;
const ll INF64 = ll(4e18) + 5;
int D[40][40];
int R[40][40];
int L;
int32_t trie[MAXN][2];
int n;
int li = 1;
void add(int x) {
int at = 0;
int K = 2 * n - 2;
for (int i = 0; i <= K; i++) {
int id = (x >> i) & 1;
if (trie[at][id] == 0) {
trie[at][id] = li++;
}
at = trie[at][id];
}
}
void limpa() {
for (int i = 0; i < li; i++) {
trie[i][0] = trie[i][1] = 0;
}
li = 1;
}
int query(int at, int x, int dep) {
int id = (x >> dep) & 1;
if (id == 0) {
if (trie[at][1]) {
return query(trie[at][1], x, dep + 1);
}
return dep;
}
int ans = dep;
if (trie[at][0])
ans = max(ans, query(trie[at][0], x, dep + 1));
if (trie[at][1])
ans = max(ans, query(trie[at][1], x, dep + 1));
while ((x >> ans) & 1)
ans++;
return ans;
}
void rec_in(int i, int j, int tar1, int tar2, int v) {
if (i > tar1 || j > tar2)
return;
if (i == tar1 && j == tar2) {
add(v);
}
int right = v | (1ll << R[i][j]);
int down = v | (1ll << D[i][j]);
rec_in(i + 1, j, tar1, tar2, down);
rec_in(i, j + 1, tar1, tar2, right);
}
int ANS = 0;
void rec_out(int i, int j, int tar1, int tar2, int v) {
if (i < tar1 || j < tar2)
return;
if (i == tar1 && j == tar2) {
ANS = max(ANS, query(0, v, 0));
return;
}
int left = v | (1ll << R[i][j - 1]);
int up = v | (1ll << D[i - 1][j]);
rec_out(i - 1, j, tar1, tar2, up);
rec_out(i, j - 1, tar1, tar2, left);
}
void solve() {
ANS = 0;
for (int i = 1; i <= li; i++)
trie[i][0] = trie[i][1] = 0;
li = 1;
cin >> n;
L = 4 * n / 3;
for (int i = 0; i < n - 1; i++) {
for (int j = 0; j < n; j++) {
cin >> D[i][j];
}
}
if (L > n) {
L--;
}
if (L > n) {
L--;
}
if (L > n) {
L--;
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < n - 1; j++) {
cin >> R[i][j];
}
}
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
if (i + j == L) {
limpa();
rec_in(0, 0, i, j, 0);
rec_out(n - 1, n - 1, i, j, 0);
}
cout << ANS << '\n';
}
signed main() {
ios::sync_with_stdio(false);
cin.tie(NULL);
int t = 1;
cin >> t;
while (t--) {
solve();
}
return 0;
}
idea: le0n, xcyle, solution: le0n, xcyle
Try to solve Problem 101 with any approach.
Can you express the states in the solution for Problem 101 with some simple structures? Maybe dp of dp?
Try finding some unnecessary states and pruning them, to knock a $$$n$$$ off the complexity.
We analyse Problem 101 first. A dp solution will be, let $$$f_{l,r,v}$$$ be the minimum number of elements left after some operations, if we only consider elements in $$$a[l:r]$$$, without creating any elements $$$>v$$$. If $$$\max(a[l:r])<v$$$, then the answer is $$$1$$$ if $$$r-l+1$$$ is odd, and $$$2$$$ otherwise. We simply repeatedly perform operations with middle element as the center. It is easy to see that this is optimal.
If $$$\max(a[l:r])=v$$$, then $$$a[l:r]$$$ will be partitioned into blocks by elements equal to $$$v$$$. Denote the length of the blocks as $$$y_1,y_2,\cdots,y_l$$$. Let $$$b_i$$$ be the number of operations that has the $$$i$$$-th element with value $$$v$$$ as its center.
We can perform a dp as follows: let $$$g_{i,j}$$$ be the minimum number of elements left if we have already considered the first $$$i$$$ blocks, and $$$b_i=j$$$.
When adding a new block, we need to know several things:
$$$[l^\prime,r^\prime]$$$, the minimum/maximum number of elements of the new block after some operations, without creating an element greater than $$$v-1$$$.
$$$j_2$$$, the value of $$$b_{i+1}$$$.
The transition of the dp will be: $$$g_{i+1,j_2}=g_{i,j_1}+cost(j_1+j_2,l^\prime,r^\prime)$$$, where $$$cost(j,l,r)$$$ is defined as follows:
The $$$cost$$$ function follows from the case where $$$\max(a)<v$$$.
Now, we have a solution to Problem 101. We now consider generalizing it to Counting 101.
We make some observations regarding the structure of $$$g$$$. If you printed a table of $$$g$$$, you would discover that for each $$$g_i$$$, if you subtract the minimum element from all $$$g_{i,j}$$$ in this row, you will get something like: $$$[\cdots,2,1,2,1,2,1,0,1,0,1,0,1,0,1,2,1,2,\cdots]$$$.
We can prove this by induction and some casework, which is omitted for brevity. If a $$$g_i$$$ satisfies this property, then we can express it with a triple $$$(l,r,mn)$$$, where $$$mn$$$ is the minimum element of $$$g_i$$$, and $$$l,r$$$ are the minimum/maximum $$$j$$$ such that $$$g_{i,j}=mn$$$.
Now that we can express the structure of each $$$g_i$$$ with a triple $$$(l,r,mn)$$$, we can run a dp of dp. Our state will be $$$dp_{i,v,l,r,mn}$$$, where $$$i$$$ is the current length, $$$v$$$ is the upper bound, and $$$(l,r,mn)$$$ describes the current $$$g$$$. For each transition, we need to enumerate $$$l^\prime,r^\prime$$$, and the new $$$(l,r,mn)$$$ can be found in $$$O(1)$$$ with some casework. This gives us an $$$O(n^6m)$$$ solution.
Now to optimize the solution. We optimize the solution by reducing the number of viable states. Suppose we have a state $$$+(l,r,mn)$$$, we claim, that the answer will remain the same if we replace it with $$$+(l,\infty,mn)+(l\bmod2,r,mn)-(l\bmod2,\infty,mn)$$$.
We prove this by examining their behaviour when we add any number of blocks after them. If the answer remains unchanged for any blocks we can add, then the claim stands. Suppose we are at $$$g_i$$$, and we will add a sequence of blocks $$$S$$$ after $$$g_i$$$. The final answer can be found by running a backwards dp similar to $$$g$$$, on $$$\text{rev}(S)$$$, and merging with $$$g_i$$$ in the middle.
If we denote the backwards dp as $$$g^\prime$$$, then the answer will be $$$\min(g_j+g^\prime_j)$$$ over all $$$j$$$. It can be shown after some brief casework (using $$$g$$$'s structure), that there exists an optimal $$$j$$$ where $$$g_{i,j}$$$ is the minimum of $$$g_i$$$, thus the answer is just a range (with a certain parity) min of $$$g^\prime$$$, plus $$$mn$$$. Because $$$g^\prime$$$ also follow $$$g$$$'s structure, any range will be first decreasing, then increasing. It can be shown with these properties, $$$\min(g^\prime[l:r])=\min(g^\prime[l:\infty])+\min(g^\prime[l\bmod2:r])-\min(g^\prime[l\bmod2:\infty])$$$. Thus, our answer will not change when substituting the states.
After substituting, the total number of different $$$l,r$$$ pairs will be $$$O(n)$$$, which yields an $$$O(n^5m)$$$ solution.
The solution can also be optimized to $$$O(n^4m)$$$ using Lagrange Interpolation, but it actually runs slower than $$$O(n^5m)$$$ because of large constants (or bad implementation by setters).
#include <bits/stdc++.h>
#pragma comment(linker, "/stack:200000000")
#pragma GCC optimize("Ofast")
#pragma GCC target("sse,sse2,sse3,ssse3,sse4,popcnt,abm,mmx,avx,tune=native")
#define L(i, j, k) for(int i = (j); i <= (k); ++i)
#define R(i, j, k) for(int i = (j); i >= (k); --i)
#define ll long long
#define vi vector <int>
#define sz(a) ((int) (a).size())
#define me(f, x) memset(f, x, sizeof(f))
#define ull unsigned long long
#define pb emplace_back
using namespace std;
const int N = 133, mod = 1e9 + 7;
struct mint {
int x;
inline mint(int o = 0) {
x = o;
}
inline mint &operator = (int o) {
return x = o, *this;
}
inline mint &operator += (mint o) {
return (x += o.x) >= mod && (x -= mod), *this;
}
inline mint &operator -= (mint o) {
return (x -= o.x) < 0 && (x += mod), *this;
}
inline mint &operator *= (mint o) {
return x = (ll) x * o.x % mod, *this;
}
inline mint &operator ^= (int b) {
mint w = *this;
mint ret(1);
for (; b; b >>= 1, w *= w)
if (b & 1)
ret *= w;
return x = ret.x, *this;
}
inline mint &operator /= (mint o) {
return *this *= (o ^= (mod - 2));
}
friend inline mint operator + (mint a, mint b) {
return a += b;
}
friend inline mint operator - (mint a, mint b) {
return a -= b;
}
friend inline mint operator * (mint a, mint b) {
return a *= b;
}
friend inline mint operator / (mint a, mint b) {
return a /= b;
}
friend inline mint operator ^ (mint a, int b) {
return a ^= b;
}
};
inline mint qpow(mint x, int y = mod - 2) {
return x ^ y;
}
mint fac[N], ifac[N], inv[N];
void init(int x) {
fac[0] = ifac[0] = inv[1] = 1;
L(i, 2, x) inv[i] = (mod - mod / i) * inv[mod % i];
L(i, 1, x) fac[i] = fac[i - 1] * i, ifac[i] = ifac[i - 1] * inv[i];
}
mint C(int x, int y) {
return x < y || y < 0 ? 0 : fac[x] * ifac[y] * ifac[x - y];
}
inline mint sgn(int x) {
return (x & 1) ? mod - 1 : 1;
}
int n, m;
mint f[N][N];
mint g[N][N];
mint h1[N][N][N];
mint h2[N][N][N];
mint pw[N][N];
int ans[N][N][N];
int main() {
ios :: sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
n = 130, m = 30;
// n = m = 10;
L(i, 0, max(n, m)) {
pw[i][0] = 1;
L(j, 1, max(n, m)) pw[i][j] = pw[i][j - 1] * i;
}
f[0][0] = 1;
int c1 = 0, c2 = 0;
L(test, 1, m) {
me(g, 0);
int up = n;
L(i, 0, up + 1) L(j, 0, i) L(l, 0, i) h1[i][j][l] = h2[i][j][l] = 0;
h2[0][0][0] = 1;
L(i, 0, up + 1) {
L(j, 0, i) L(l, 0, i) h1[i][j][l & 1] -= h1[i][j][l];
L(j, 0, i) {
for (int l = (i - j) & 1; l <= i; l += 2)
if (h1[i][j][l].x) {
L(k, 0, up - i) {
if (l > k) {
int tr = k - !(l & 1);
if (tr < 0)
h2[i + k + 1][j + 3][0] += h1[i][j][l] * pw[test - 1][k];
else
h2[i + k + 1][j + 2][tr] += h1[i][j][l] * pw[test - 1][k];
} else {
h2[i + k + 1][j + 1][k - l] += h1[i][j][l] * pw[test - 1][k];
}
}
}
for (int r = (i - j) & 1; r <= i; r += 2)
if (h2[i][j][r].x) {
int l = r & 1;
L(k, 0, up - i) {
if (l > k) {
int tr = k - !(r & 1);
if (tr < 0)
h2[i + k + 1][j + 3][0] += h2[i][j][r] * pw[test - 1][k];
else
h2[i + k + 1][j + 2][tr] += h2[i][j][r] * pw[test - 1][k];
} else {
h2[i + k + 1][j + 1][k - l] += h2[i][j][r] * pw[test - 1][k];
L(d, r + 1, k) if (f[k][d].x)
h1[i + k + 1][j + 1][d - r] += h2[i][j][r] * f[k][d];
}
}
}
}
}
// cout << "H = " << h[1][1][0][0].x << endl;
L(i, 1, up + 1)
L(j, 1, i) {
L(l, 0, i) if (h1[i][j][l].x) {
if (!l)
g[i - 1][j - 1] += h1[i][j][l];
else
g[i - 1][j - 1 + (l % 2 == 0 ? 2 : 1)] += h1[i][j][l];
}
L(r, 0, i) if (h2[i][j][r].x) {
if (!(r & 1))
g[i - 1][j - 1] += h2[i][j][r];
else
g[i - 1][j - 1 + (r % 2 == 0 ? 2 : 1)] += h2[i][j][r];
}
}
L(i, 1, up) {
mint vl = 0;
if (i == 1)
vl = test;
else if (i % 2 == 1) {
vl += pw[test - 1][i];
L(p, 1, i - 2) {
int l = p, r = i - p - 1;
if (l > r)
swap(l, r);
L(j, 1, l) {
vl += f[r][j] * pw[test - 1][l];
}
}
}
g[i][1] = vl;
mint sum = 0;
L(j, 1, i) sum += g[i][j];
int pos = (i & 1) ? 3 : 2;
g[i][pos] += pw[test][i] - sum;
}
swap(f, g);
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= n; j++) {
ans[test][i][j] = f[i][j].x;
}
}
}
// cout << "clock = " << clock() << endl;
int T;
cin >> T;
while (T--) {
int N, M;
cin >> N >> M;
L(i, 0, (N - 1) / 2)
cout << ans[M][N][N - i * 2] << " ";
cout << '\n';
}
return 0;
}










Woah, I solved A,B,C all through guessing and became purple!
You really solved E first... :skull:
I got stuck for an hour trying to prove the earlier problems XD
I created video editorial for E: Cosmic Rays.
Why this solution of mine for C is giving WA on test5? 275844339
Check for integer overflow
sqrt can cause precision loss, i recommend you eliminate it completely
how will we check then?
My approach : If after distance(d) time, if our destination points becomes part of any of the circle then the answer is NO otherwise YES.
you can just compare the squared distance, you end up squaring it again after taking the square root anyways
thank you! it worked :)
by the way, just want to understand how to identify such things?
For me, I used long double in C++ and it worked.
lol, you can solve D1 in $$$O(N*Q)$$$ with pragmas: 275797240
Also you can use segment tree too for E: 275831791
I also tried spamming pragmas but I got TLE on pretest 13 :) https://mirror.codeforces.com/contest/2002/submission/275836926
diko hacked it. Thanks
I solved E using stack, I think E is much easier than D1, D2 took me only 15 mins to solve E. https://mirror.codeforces.com/contest/2002/submission/276392625
Can someone try hacking my solution to E? I solve for each value separately and use RMQ to keep track of merging blocks, but I believe my code is O(N^2 log N) if one value appears lots of times, the first and last occurrence of that value have high a_i, and all intermediate occurrences have very low a_i. 275860315
Only solve A, B.
I am too weak. T^T
In problem D2 check 1, can someone explain how the merge step works? ("merge the subtree of u into a large node with size siz_u")
I don't understand why it is sufficient to just maintain "bad" children, instead of maintaining information for the entire subtree.
Let's note the following $$$pos_x$$$ : position of $$$x$$$ in $$$p$$$
$$$sub_x$$$ subtree size of x
For D1 consider some node $$$x$$$ , we call node $$$x$$$ valid if the positions of its children in the permutation are $$${pos_x +1 , pos_x + t + 1}$$$ where t is the subtree size of one of the children.
A dfs order is valid iff all nodes are valid and $$$p_1 = 1$$$
So we can maintain a set for bad nodes $$$bad$$$ When we swap two values $$$p_x , p_y$$$ it only affects $$$p_x , p_y$$$ and their parents (because $$$pos_{p_x}$$$ becomes $$$y$$$ and vice versa)
So we can check easily in D1
For D2 you should maintain a set {$$$pos_{child} , child $$$} for each node $$$x$$$ . Node $$$x$$$ is valid iff (*) for each two adjacent positions of children $$$c_i$$$ , $$$c_{i+1}$$$ in the set $$$pos_{c_{i+1}} - pos_{c_i} = sub_{c_i}$$$ and $$$pos_{c_1} - pos_x = 1$$$ Thus we can maintain also a set of bad children (who don't satisfy (*)) in each node
And when we update we only remove and insert new values in the set
Finally if the set of bad children of a node is empty than erase this node from $$$bad$$$ otherwise insert it.
Thanks! While going through others' implementations I discovered that Um_nik's submission implements this idea nicely.
I suppose, this part is just about proving that subtree dfs log places next to the parent node dfs log. So there's no merging part when talking about solution.
Actually, I don't understand how to keep tracking "bad" nodes with sets on D2. I would be glad if someone would explain this part. Can't understand author's code ideas.
P.S.: Sorry, don't refresh the page too long , thaks for explaining!
the image in c's tutorial is not visible
Why this solution of mine for D1 is giving TLE on test9 and it's O(n*q)? My Solution
Because n*q is too big
i thought that too, but i asked bcos i see people saying they solved it in O(n * q)
I am really dumb .
But Why CD = AD in tutorial of C . I don't understand that
could anyone explain that pls.
I think that CD = AD represent the point where we intersect with a circle since our starting point A has the same distance to D as does the circle's center C.
understand it in a way that the speed of expansion of circles is same as walking speed of the guy and thus the circles radius at any instant would be same as the distance covered by the guy till that instant which implies AD=CD
Alternative (possibly wrong?) solution for D2:
Firstly, check that for each $$$i$$$ from $$$2$$$ to $$$n$$$ $$$p_{i - 1}$$$ is the parent of $$$p_i$$$ except the case when $$$p_{i - 1}$$$ is a leaf.
Also check that for each $$$i$$$ the position of $$$i$$$ in $$$p$$$ is greater than the position of its parent.
Check that the multiset $$$S = \{ LCA(p_1, p_2), LCA(p_2, p_3), \cdots, LCA(p_{n - 1}, p_n) \} $$$ matches with such multiset of any valid DFS order (intuition: virtual trees). It can be easily checked by maintaining the multiset hash.
Here is my implementation: 275842859. Feel free to uphack it.
UPD. It seems that the second condition is unnecessary: 275927827. Now my solution looks similar to the Check 2 in the editorial as songhongyi pointed below (thanks for it). I think the first condition is a "weaker" version of Check 2 and the third condition makes my solution work somehow by making the first one "stronger". I still don't know how to prove it though.
UPD 2. Actually the second condition is necessary but the first one isn't. Now it seems less similar to Check 2.
This solution is very similar to check2. I suspect it's correct and should be provable in a similar way.
le0n failed to hack it so it must be true.
The check2 is actually equivalent to $$$p_1=1$$$ and $$$\operatorname{LCA}(p_i,p_{i+1})=fa(p_{i+1})$$$ forall $$$1\le i\le n$$$. Your third condition is actually $$$ \{ {\operatorname{LCA}(p_i,p_{i+1})} \} =\{fa(p_{i+1})\}$$$, which is obviously weaker than check2. But I'm sure it is equivalent to check2 with your second condition.
Could anyone write out the proof by induction in B? I'm not sure how to prove it...
I didn't really understand the subarray thing in the editorial. The way I see it is:
Suppose Bob can mimic Alice's move when there are $$$n$$$ elements. There are only two ways for this to happen (let $$$A = a_1 \dots a_n$$$, $$$B = b_1 \dots b_n$$$):
If any of the above cases happen, nothing has changed in the game and we keep going, now with $$$n-1$$$ elements.
If at any moment none of the cases above match, it means Alice has at least one endpoint element which Bob does not (let it be $$$x$$$). Bob cannot pick $$$x$$$ right after Alice, so he takes any one of his endpoint elements (let it be $$$y \neq x$$$). Now Alice can easily win by picking all her left elements except $$$y$$$, because at the end of the game, Alice will have $$$y$$$ left but Bob already deleted it, so the last elements cannot be equal.
If the game keeps going with one of the two cases described initially, Bob can always mimic Alice's move, so Alice cannot win. These two cases can only happen when the whole arrays $$$A$$$ and $$$B$$$ are equal or one is the reverse of the other.
Thank you so much!
I wish they had elaborated why the interval condition was "intuitive to see".
Here is my proof. If there is a pair of neighbors in array A that are not neighbors in B then Alice wins. She just needs to remove the elements until only those two elements remain. Then after Bob's move his remaining two elements would not be the same as the two Alice's elements, and on the following move Alice can leave an element that Bob does not have. So, for Bob to win every pair of neighbors in A need to be neighbors in B. It is easy to show that it can only happen if B is equal to A or its reverse, depending on the order in B of the first two elements of A.
What is $$$fa$$$ mentioned in Problem-D Check 2?
$$$fa(p_{i+1})$$$ must be ancestor of $$$p_i$$$.
the father(parent) of $$$p_{i+1}$$$ on the tree.
My Insights for A,B,C
Observed that answer is $$$\min(n,k) \cdot \min(m,k)$$$
Total complexity is $$$\mathcal{O}(1)$$$
Since We're performing optimally we'll keep removing from left or right thus
Thus Bob can win only and only if $a$ is the same as $$$b$$$ or $$$a=b^{-1}$$$ i.e. $$$b$$$ reversed.
Total complexity is $$$\mathcal{O}(n)$$$
The $$$mindist$$$ that is possible is $$$\min_{i=1}^n \sqrt{x_i^2+y_i^2}$$$ overall points , and the distance needed to connect $$$(x_s,y_s)$$$ and $$$(x_t,y_t)$$$ is $$$\sqrt{(x_s-x_t)^2+(y_s-y_t)^2}$$$ , let's call it $$$d$$$ , we must have $$$\text{mindist} \le d$$$ so that it's possible to connect $$$(x_s,y_s)$$$ and $$$(x_t,y_t)$$$ without intersection of circles.
Don't use square root for avoiding square root errors , it's enough to store $$$(\Delta x)^2+(\Delta y)^2$$$
Total complexity is $$$\mathcal{O}(n)$$$
I didn't solve any of BC without guessing (I proved them) ; If I guessed them then specialist was in hand for real.
How did you come up with the conclusion of A? I turn to solve B/C instead.
I tried to come up with something related about multiplication of numbers
You can see the cases like this
I think the observing the thing described in the spoiler is enough to come up with
smart!
My idea for D1 was that it looks like a segment tree: Store in each node if that subtree makes sense or not, and the maximum index in that subtree, and of course the index of the node in the permutation. Then on update query, it takes at most O(log n) updates like a segment tree, by moving up and calling combine function on the 2 children of the current node until reaching root. Then the root has the answer, by just checking if it makes sense. Combine function: to get maximum index just max the maximum index of both children and your index, to see if it makes sense one of the children's index must be 1 more than the node's index, and then the other's index must be 1 more than the maximum index of the first child so it forms a dfs order that makes sense, and of course both subtrees must make sense (AND them together). Time complexity: O(n + q log n)
In D check 1 the editorial specifies this condition:
In the code solution, a different, easier check is made:
Here
son[x]includes ordered indices of $$$x$$$'s children in the permutation. Therefore, it is only checking the editorial condition for the furthest child in the permutation, and that the closest child in the permutation has an index not less than the one $$$x$$$ itself has. Can someone explain how these conditions are equivalent to the editorial? In fact I tried to check the editorial condition directly in my code but got TLE probably due to constant factor.editorial should have cared to explain that.
Nevertheless, here we go.
Lets prove it for any node $$$u$$$.
Assume that condition is satisfied for all immediate children $$$v$$$ of $$$u$$$.
it means, for any immediate child $$$v$$$ of $$$u$$$, the range $$$[posv,posv+sizv−1]$$$ will contain whole subtree of $$$v$$$, and nothing else.
So, the point is, for any two immediate child $$$v1$$$ and $$$v2$$$, their range is non intersecting. ($$$[posv1,posv1+sizv1−1]$$$ & $$$[posv2,posv2+sizv2−1]$$$). If the ranges are non intersecting, then we can just check the first and last range, and if they are contained within $$$[posu,posu+sizu−1]$$$, then all other are forced to contain within it.
Please correct me if I'm wrong, but I think you're only proving one side of the equivalence, namely editorial check implies code check. In fact we would be more interested in the other implication ( code check implies editorial check ), since the code check at first glance looks like a weaker condition. That is, for a single node it doesn't make much sense for the checks to be equivalent, but rather the fact that this weaker check works for all nodes at the same time might be what actually makes it equivalent.
May be, I should have also cared to explain more.,
I didnt prove editorial check implies code check, that is noobest thing i can comment.
Given that code check is satisfied for any $$$u$$$, and all nodes in its subtree, then it implies that
Exactly all nodes in subtree of u are within [posu,posu+sizu−1], and nothing else. And this is not just for u, but also for all nodes in subtree of u.Which also equivalent to editorial check.By induction.
Lets say code check is satisfied for all nodes in subtree of $$$u$$$, except $$$u$$$, we didnt check for $$$u$$$ yet.
So we assume that for each immediate child $$$v$$$ of $$$u$$$, all nodes in their subtree are within $$$[posv,posv+sizv−1]$$$, and nothing else.
which means each of those ranges by immediate child of $$$u$$$ are non intersecting and continous. This is the key part.
Now we are coming for $$$u$$$, Say $$$vl$$$ as leftmost position having $$$v$$$ out of all immediate child of $$$u$$$ and $$$vr$$$ as rightmost. And if $$$posvl$$$ and $$$posvr+sizvr-1$$$ are within $$$[posu,posu+sizu−1]$$$, then it indirectly implies that all other $$$[posvm,posvm+sizvm−1]$$$ are also within the $$$u$$$ range, as $$$posvl$$$ <= $$$posvm$$$ <= $$$posvr$$$ and $$$posvm+sizvm-1$$$ cant intersect and cross the $$$vr$$$.
Now, due to size constraint, if all $$$v$$$ ranges are within $$$[posu,posu+sizu−1]$$$, it means they are completely filling the range $$$[posu,posu+sizu−1]$$$ and nothing else can be inside it.
By, induction this will propagate until root node.
checking for all immediate child $$$v$$$ of $$$u$$$, whether $$$[posv,posv+sizv−1]$$$ contained within $$$[posu,posu+sizu−1]$$$
checking only for first and last $$$v$$$.
Ok I guess I didn't understand the induction right. I got it now. Thank you!
How is F2 harder than F1? I don't see any difference, only tighter time limits maybe. Can someone explain why F2 is considered harder than F1?
Quoting editorial for D2:
Can you tell me what does the notion $$$fa(p_{i+1})$$$ mean? I don't think I have seen it being declared anywhere in the tutorial. Thank you in advance.
It means the father of $$$p_{i+1}$$$. Apparently it's not as widespread as I thought. I've added an explanation.
I see, thanks.
Can anybody explain the proof for C? I get the part where CD = AD and the CD > CB-DB part, but everything else kinda just falls apart... I've forgotten everything about proofs from geometry class
I can't understand this proof either, but if you look at the conclusion directly, it will be obvious that if the distance from the center of the circle to the target is less than or equal to the distance from the starting point to the target, it is obvious that the boundary of the circle will be touched before (and when you reach this point).
Solved ABCD1 and became specialist.
what does this line mean in editorial of $$$H$$$?
Let b_i be the number of operations that has the element equal to v after block y_i as its centerI couldn't understand the rest of the editorial because of that
WOW!You are very good! But could you give me some exegesis in the H code?
why was E placed after D?
https://mirror.codeforces.com/blog/entry/132346?#comment-1182297
D1 is much easier than E, D2 is also not much harder imo but D1 is sufficient reason anyways
but shouldn't the point sums be nondecreasing? just by convention maybe
there's definitely been instances where F1 is easier than E and such
for the following test case for D2,
check 1 outputs NO NO but check 2 (and other ACs) output NO YES and i think it should be NO YES. the way siz is calculated in check 1 makes siz[1] = 6 and siz[3] = 3 but shouldn't they be siz[1] = 7 and siz[3] = 4?
Edit: nvm the constraint ai < i is not satisfied for this tree so it's a wrong tc
$$$1 \le a_i \lt i$$$, but in your case $$$a_3 = 7$$$ so it's invalid.
Solution 3 in problem F2 is interesting. Despite $$$L = 50$$$ is already hacked, higher $$$L$$$ should still yield an AC (with the cost of praying that one's code wouldn't TLE).
A loose upperbound by me, with $$$L = 125$$$: 276065570
I wonder how far could the uphack raise up "cheeseable" lowerbound value for $$$L$$$.
Could anyone explain how we are supposed to preprocess GCD as mentioned in F1 solution?
I didn't preprocess GCD, my solution got passed
My F1 also passed using the normal one. But for F2, I had to use custom binary gcd function (which I copied from one of the CF blogs). That's why I asked if it was possible to preprocess the gcd and then find them in constant time. It will be a huge optimization, nearly 20 times for the given constraints.
For problem D, the following check is also sufficient:
It's just check2 written in another form.
Hey, can you explain me how can I use segment tree to solve the problem D2. The authors solution mentions that we can impose some check on each node in the permutation.
Specifically, For every
u, all of its childrenvsatisfiesAnd, we can maintain this check by keeping track of the number of
uwhich violates this condition, and check for eachuusing sets.First of all, how can we do this using sets, and how can we do this using segment tree. I tried thinking a lot, but I could only think of maintaining a segment tree using dfs entry time. So each segment node in the segment tree contains a set/vector containing entry times for each tree node in this segment. And for swapping part, I could do it like replacing the entry time for swapped nodes in the set of their respective segments.
Then how can I perform verifying this check for each node using this segment tree? This is where I'm getting stuck. Can you help me out, Please.
Editorial should have mentioned that, they compare only smallest and largest $$$posv$$$ to see if they are within $$$[posu,posu+sizu−1]$$$, rather than all its childs. see: https://mirror.codeforces.com/blog/entry/132569?#comment-1182635
Yeah, I get it that checking the first and last child range is equivalent to checking all of children of u. Because the set stores the position of each node in sorted order.
And we can easily perform swapping by first deleting the position of a node from its parent's children set and then add the swapped node position to it, and again the set would maintain all the positions in sorted order. The number of good nodes are decreased for now, as we need to check again after swap if they become good nodes.
Now after swap, we only need to check for the (parent(a), a) and (a, children(a)) for all children of a. Similarly for (parent(b), b) and (b, children(b)) for all the children of b, for the condition of a good node. Because we want to see if after swap, the node is still contained in its parent range, and the node still contains all of its children within its range. If yes, then the number of good nodes increases by one each time for all these 4 pairs, otherwise not. And after each query, we check if all n nodes are good nodes or not. And we print the answer accordingly.
Can someone explain why this solution for D is timing out? 276371875
I am trying to implement Um_nik's idea from his submission: 275817851
Interesting, submitting your solution in GCC 7-32 yielded TLE while GCC 13-64 yielded RTE.
Huge red flag of undefined behaviors right here, though I can't yet tell where it was.
Alternative (maybe easier) solution for D :
let s[x] = {{j1,u1}, {j2,u2},... } be the set of indices and node id of the children of the node x, pos[x] the position of node x in P, and siz[x] the size of the subtree of node x.
It suffices to check that for all i from 1 to n : pos[x] = min(s[x]) + 1 , and for all i from 1, s[x].size() — 1 : Ji+1 — Ji == siz[Ui] meaning the positions of the children of x when sorted should have the difference of siz[u] where u is the node with smaller pos.
Ask a question to the time complexity of G.
this formula $$$2^{2B}+2^{2-B}$$$
but you use some calculus you know B=1/3 it's minimum. not B=2/3
for f1, if you let p be the largest prime <= n, then x<=p or y<=p is possible.