Except hints/solutions, I try to add a "general idea" section discuss about some general strategy and standard ideas used to solve the problem, hope you would like it :)
idea & solution: Misuki
What's the most obvious lower bound of the answer?
Is the lower bound achievable?
One standard way to solve optimization problem is to make observation on lower(upper) bound of the answer and prove such bound is achievable, it's useful in lot of problems.
Let $$$x$$$ be one of the most frequent elements in $$$a$$$, then the answer must be at least $$$(n - \text{frequency of } x)$$$, and this lower bound is always achievable by keep erasing a non-$$$x$$$ element from $$$a$$$, and we can prove it's always possible to do so.
proof:
If all elements of $$$a$$$ are $$$x$$$, we are done. Otherwise, let $$$y$$$ denote all the elements that are not $$$x$$$, then $$$a$$$ would have some subarray of the form $$$x \ldots x, y \ldots y, x \ldots x$$$. In this subarray, there must exist adjacent elements that satisfy $$$a_i \leq a_{(i \bmod m) + 1}$$$, otherwise we would have $$$x > y > \ldots > y > x$$$ implying $$$x > x$$$ which leads to a contradiction.
#include <algorithm>
#include <iostream>
#include <vector>
using namespace std;
int main() {
ios::sync_with_stdio(false), cin.tie(NULL);
int t; cin >> t;
while(t--) {
int n; cin >> n;
vector<int> a(n);
for(int &x : a) cin >> x;
vector<int> freq(n + 1);
for(int x : a) freq[x]++;
cout << n - (*max_element(freq.begin(), freq.end())) << '\n';
}
}
2001B - Сгенерируйте перестановку
idea & solution: Misuki
Write a few small cases (ex. $$$n = 3, 4, 5$$$) and play with it, can you notice something interesting about the cost function?
Write a few examples and play with it is a good start to solve ad-hoc problems.
Consider subtask — decision version of the problem (i.e. yes/no problem) as follow: "Given a fixed $$$p$$$, check if this permutation is valid."
The above problem would reduce to finding minimum number of carriage return operations needed for each typewriter.
Now you know how to solve above problem, do you notice something interesting about the cost function?
In lot of problems, decision version of the problem is usually a useful subtask to consider.
Consider the cost function:
Let $$$c_1, c_2$$$ denote the minimum number of carriage return operations needed to make $$$a = p$$$ if Misuki is using first/second typewritter. Let's consider how to calculate them.
For $$$c_1$$$, we need to do carriage return operation whenever the position of value $$$x + 1$$$ is before $$$x$$$, for all $$$x \in [1, n - 1]$$$, so $$$c_1 = (\text{#}x \in [1, n - 1] \text{ such that } \mathrm{pos}_x > \mathrm{pos}_{x + 1})$$$.
Similarly, $$$c_2 = (\text{#}x \in [1, n - 1] \text{ such that } \mathrm{pos}_x < \mathrm{pos}_{x + 1})$$$.
Since for $$$x \in [1, n - 1]$$$, either $$$\mathrm{pos}_x < \mathrm{pos}_{x + 1}$$$ or $$$\mathrm{pos}_x > \mathrm{pos}_{x + 1}$$$ would hold, so we have $$$c_1 + c_2 = n - 1$$$, which is a constant, and $$$c_1 = c_2 \leftrightarrow c_1 = \frac{n - 1}{2}$$$, which only has solution when $$$n$$$ is odd, and such $$$p$$$ can be constructed easily (for example, $$${n - 1, n, n - 3, n - 2, ..., 4, 5, 2, 3, 1}$$$).
#include <iostream>
#include <numeric>
#include <vector>
using namespace std;
int main() {
ios::sync_with_stdio(false), cin.tie(NULL);
int t; cin >> t;
while(t--) {
int n; cin >> n;
if (n % 2 == 0) {
cout << -1 << '\n';
} else {
vector<int> p(n);
iota(p.begin(), p.end(), 1);
for(int i = 1; i < n; i += 2)
swap(p[i], p[i + 1]);
for(int i = 0; i < n; i++)
cout << p[i] << " \n"[i + 1 == n];
}
}
}
idea: feecle6418, solution: Kaey
Imagine we have $$$n$$$ isolated vertices initially, can you find any edge connect two component using reasonable number of queries?
Use binary search.
It's easy to verify that querying $$$a$$$ and $$$b$$$ will return the midpoint of the path between $$$a$$$ and $$$b$$$. In case the path has odd length, the node closer to $$$a$$$ of the two central nodes will be returned.
We will now construct the tree by expanding a connected component. Let $$$A = \{1\}$$$ and $$$B = \{2,\ldots,n\}$$$. While $$$B$$$ is not empty, choose any $$$b \in B$$$ and $$$a \in A$$$. Let $$$P$$$ be the path between $$$a$$$ and $$$b$$$. By construction, $$$P$$$ will consist of a prefix contained in $$$A$$$ and a suffix contained in $$$B$$$. We can binary search for the first $$$i$$$ such that $$$P_i \in B$$$.
This will take at most $$$\lceil log(|P|) \rceil + 2$$$ queries. Then, $$$(P_{i-1}, P_i)$$$ will be an edge of the tree, so we will set $$$A = A \cup {P_i}$$$ and $$$B = B \backslash {P_i}$$$.
The total number of queries will be smaller than $$$n \lceil log(n) \rceil + 2n = 12000$$$.
Consider we have $$$n$$$ isolated vertices initially, and try to keep finding an edge connect two different component.
Assume $$$u, v$$$ is at different component, then we have the following possible cases for the answer $$$x$$$.
- $$$x = u$$$: which means $$$u, v$$$ are connected by an edge and we are done.
- $$$x$$$ belongs to same component of $$$u$$$, seting $$$u := x$$$.
- $$$x$$$ belongs to same component of $$$v$$$, seting $$$v := x$$$.
- $$$x$$$ belongs to other component than $$$u, v$$$, in such case, either setting $$$u := x$$$ or $$$v := x$$$.
in case 1. we are done, and in case 2, 3, 4, we shorten the distance between $$$u, v$$$ by about half while keeping them not belongs to same component, so we can find an edge connect two component in $$$O(\lg n)$$$ queries and we are done.
#include <iostream>
#include <system_error>
#include <vector>
using namespace std;
int qry(int a, int b){
cout << "? " << a+1 << ' ' << b+1 << endl;
fflush(stdout);
int r; cin >> r;
return r-1;
}
void solve(){
int N; cin >> N;
vector<int> in_tree(N, 0), stk;
for (size_t i = 1; i < N; ++i)
stk.push_back(i);
in_tree[0] = 1;
vector<pair<int, int>> edges;
while(!stk.empty()){
int n = stk.back();
stk.pop_back();
if(in_tree[n])continue;
int l = 0, r = n;
while(1){
int q = qry(l, r);
if(q == l){
in_tree[r] = 1;
edges.push_back({l, r});
break;
}
if(in_tree[q])l = q;
else r = q;
}
stk.push_back(n);
}
cout << "! ";
for(auto [x, y]: edges)cout << x+1 << ' ' << y+1 << ' ';
cout << endl;
}
int main(){
int t; cin >> t;
while(t--)solve();
}
#include <iostream>
#include <numeric>
#include <vector>
#include <array>
using namespace std;
int query(int u, int v) {
cout << "? " << u + 1 << ' ' << v + 1 << '\n';
int x; cin >> x;
return x - 1;
}
int main() {
int t; cin >> t;
while(t--) {
int n; cin >> n;
vector<array<int, 2>> e;
vector<int> c(n);
iota(c.begin(), c.end(), 0);
auto addEdge = [&](int u, int v) {
e.push_back({u, v});
vector<int> cand;
for(int i = 0; i < n; i++)
if (c[i] == c[v])
cand.emplace_back(i);
for(int i : cand)
c[i] = c[u];
};
for(int i = 0; i < n - 1; i++) {
int u = 0, v = 0;
while(c[v] == c[u]) v++;
int x;
while((x = query(u, v)) != u) {
if (c[u] == c[x]) u = x;
else v = x;
}
addEdge(u, v);
}
cout << "!";
for(auto [u, v] : e) cout << ' ' << u + 1 << ' ' << v + 1;
cout << '\n';
}
}
2001D - Самая длинная подпоследовательность
idea & solution: Misuki, tester's code: SorahISA
Forget about minimize lexicographical order. What's the size of longest $$$b$$$ we can get?
It's the number of different elements. Try to minimize/maximize first element in $$$b$$$ without reducing the max size of $$$b$$$ we can get.
When solving problem asking for minimize/maximize lexicographical order of something, we can often construct them by minimize/maximize first element greedily.
Consider subtask:
Let's ignore the constraint where $$$b$$$ should be lexicographically smallest. How can we find the length of $$$b$$$?
Apparently, it is the number of distinct elements in $$$a$$$. Let's call it $$$k$$$.
Construct $$$b$$$ from left to right without worsening the answer:
Now we know how to find the maximum possible length of $$$b$$$. Let's try to construct $$$b$$$ from left to right without worsening the answer, and greedily minimize its lexicographical order. Assume we pick $$$a_i$$$ as the $$$j$$$-th element in $$$b$$$, then there should be $$$k - j$$$ distinct elements in the subarray $$$a[i + 1, n]$$$ after deleting all elements that appear in the subarray $$$b[1, j]$$$.
Assume we already construct $$$b_1, b_2, \ldots, b_j$$$ where $$$b_j = a_i$$$ and we want to find $$$b_{j + 1}$$$, and let $$$l_x$$$ be the last position where $$$x$$$ occurs in the subarray $$$a[i + 1, n]$$$ or $$$\infty$$$ if it doesn't exist, then we can choose anything in $$$a[i + 1, \min\limits_{1 \le x \le n}(l_x)]$$$. And to minimize lexicographical order, we need to choose the maximum element in it if $$$(j + 1)$$$ is odd, or the minimum element otherwise. If there are multiple of them, choose the leftmost one of them is optimal since we would have a longer suffix of $$$a$$$ for future construction.
Then observe for the candidate window (i.e. $$$a[i + 1, \min\limits_{1 \le x \le n}(l_x)]$$$), its left bound and right bound are non-decreasing, so we can use priority queues or set to maintain all possible candidates by storing $$$(a_{pos}, pos)$$$, and another priority queue or set to maintain all $$$l_x > i$$$. And the total time complexity is $$$O(nlgn)$$$.
#include <iostream>
#include <vector>
#include <queue>
#include <array>
#include <climits>
using namespace std;
int main() {
ios::sync_with_stdio(false), cin.tie(0);
int t; cin >> t;
while(t--) {
int n; cin >> n;
vector<int> a(n);
for(int &x : a) {
cin >> x;
x--;
}
vector l(n + 1, INT_MAX);
for(int i = 0; i < n; i++)
l[a[i]] = i;
priority_queue<int, vector<int>, greater<int>> ls(l.begin(), l.end());
priority_queue<array<int, 2>, vector<array<int, 2>>, greater<array<int, 2>>> mx_cand, mn_cand;
vector<bool> used(n, false);
for(int i = 0; i <= ls.top(); i++) {
mx_cand.push({-a[i], i});
mn_cand.push({a[i], i});
}
vector<int> b;
int i = 0;
while(!mn_cand.empty()) {
auto [x, pos] = (b.size() % 2 == 0 ? mx_cand.top() : mn_cand.top());
if (b.size() % 2 == 0) {
mx_cand.pop();
x *= -1;
} else {
mn_cand.pop();
}
b.emplace_back(x);
i = pos + 1, used[x] = true;
while(ls.top() != INT_MAX and used[a[ls.top()]]) {
int j = ls.top(); ls.pop();
for(int k = j + 1; k <= min(ls.top(), n - 1); k++) {
mx_cand.push({-a[k], k});
mn_cand.push({a[k], k});
}
}
while(!mx_cand.empty() and (used[-mx_cand.top()[0]] or mx_cand.top()[1] < i)) mx_cand.pop();
while(!mn_cand.empty() and (used[mn_cand.top()[0]] or mn_cand.top()[1] < i)) mn_cand.pop();
}
cout << b.size() << '\n';
for(int i = 0; i < b.size(); i++)
cout << b[i] + 1 << " \n"[i + 1 == b.size()];
}
}
#include <cstdint>
#include <iostream>
#include <set>
#include <vector>
using namespace std;
void solve() {
int N; cin >> N;
vector<int> A(N);
for (int &x : A) cin >> x, --x;
vector<int> cnt(N, 0), is_last(N, 0), last_pos(N, -1);
for (int i = N-1; i >= 0; --i) {
if (!cnt[A[i]]++) is_last[i] = 1, last_pos[A[i]] = i;
}
vector<int> ans;
multiset<int> st;
int l = 0, r = -1, flag = 0;
while (r+1 < N) {
while (r+1 < N and (r == -1 or !is_last[r])) {
++r;
if (is_last[last_pos[A[r]]]) st.emplace(A[r]);
}
if (st.size()) {
ans.emplace_back(flag ? *begin(st) : *rbegin(st)), flag ^= 1;
is_last[last_pos[ans.back()]] = 0;
while (A[l] != ans.back()) {
if (auto it = st.find(A[l++]); it != end(st)) st.erase(it);
}
st.erase(A[l++]); // no find
}
}
int M = ans.size();
cout << M << '\n';
for (int i = 0; i < M; ++i) cout << ans[i] + 1 << " \n"[i == M-1];
}
int32_t main() {
ios_base::sync_with_stdio(0), cin.tie(0);
int t = 1; cin >> t;
for (int _ = 1; _ <= t; ++_)
solve();
return 0;
}
2001E1 - Детерминированная куча (простая версия)
idea & solution: Misuki
Consider subtask — decision version of the problem (i.e. yes/no problem) as follow: "Given a sequence $$$a$$$ resulting from $$$k$$$ operations, check whether such $$$a$$$ is a deterministic max-heap.", what property $$$a$$$ should have?
Try to fix the position of leaf being popped, what property are needed on the path from root to it?
Does it really matter where the leaf being popped lies important?
Try to count the number of $$$a$$$ where the first leaf being popped is fixed at one position using DP.
Try to use DP to track the path of elements being popped and count number of possible $$$a$$$ satisfy the property.
Again, in lot of problems, decision version of the problem is usually a useful subtask to consider. And it's especially useful in counting problems about giving some operation and ask you to count the number of possible outcomes.
Consider properties of the result sequence:
Since there may be multiple ways to apply operations to make the same heap, let's consider the decision version of the problem instead of counting the operation sequence directly. That is, "Given a sequence $$$a$$$ resulting from $$$k$$$ operations, check whether such $$$a$$$ is a deterministic max-heap.", and try to figure out what properties are needed.
Rephrase of problem:
Let $$$v = 2^{n - 1}$$$ be the only leaf such that after popping one element from the top, every element on the path between $$$1$$$ and $$$v$$$ would be moved upward, then the condition of a deterministic max-heap can be rephrased as follows:
- $$$a_1 = k$$$
- $$$a_{v} \ge a_{2v} + a_{2v + 1}$$$, for any $$$v$$$ ($$$1 \le v < 2^{n - 1}$$$)
- $$$a_{2\cdot 2^k} > a_{2 \cdot 2^k + 1}$$$, for any $$$k$$$ ($$$0 \le k \le n - 2$$$)
So we can see that for any $$$k$$$ ($$$0 \le k \le n - 2$$$), the number of operations done in the subtree of $$$2\cdot 2^k$$$ should be greater than the number of operations done in the subtree of $$$2 \cdot 2^k + 1$$$, and we don't care much about how these operations distribute in the subtree of $$$2 \cdot 2^k + 1$$$ as long as 3. holds. Let's call such subtree "uncritical".
Apply counting:
For any uncritical subtree with size $$$sz$$$, if we do $$$x$$$ operations under it, there are $$$\binom{x + (sz - 1)}{x}$$$ ways to do so.
Now we can use dp to consider all valid $$$a$$$ we can get by enumerating the number of operation done on each vertex on the path from $$$1$$$ to $$$2^{n - 1}$$$ and all uncritical subtree.
Let $$$dp[i][j]$$$ be the number of different $$$a$$$ we can get by $$$j$$$ operations on the subtree with size $$$2^i - 1$$$, then we have
base case: $$$dp[1][j] = 1, \forall j \in [0, k]$$$
transition: $$$dp[i + 1][l] \text{ += } dp[i][j] \times \binom{x + (2^i - 2)}{x} ,\forall x \in [0, j), l \in [j + x, k]$$$
using prefix sum, we can optimize the above dp to $$$O(nk^2)$$$, and the number of deterministic max-heap where vertex $$$2^{n - 1}$$$ would be pulled up is $$$dp[n][k]$$$.
Make use of symmetry:
Finally, due to the symmetry property of a perfect binary tree, the number of deterministic max-heap where $$$v$$$ would be pulled are equal for all possible $$$v$$$, so the final answer we want would be $$$dp[n][k] \times 2^{n - 1}$$$.
#include <iostream>
#include <vector>
using namespace std;
using ll = long long;
int binpow(ll a, ll b, ll p) {
ll c = 1;
while(b) {
if (b & 1) c = c * a % p;
a = a * a % p, b >>= 1;
}
return c;
}
int main() {
int t; cin >> t;
while(t--) {
int n, k, p; cin >> n >> k >> p;
vector<ll> fac(k + 1, 1);
for(int i = 1; i <= k; i++) fac[i] = fac[i - 1] * i % p;
vector<ll> faci(k + 1);
faci[k] = binpow(fac[k], p - 2, p);
for(int i = k - 1; i >= 0; i--) faci[i] = faci[i + 1] * (i + 1) % p;
vector<ll> pow2(n + 1, 1);
for(int i = 1; i <= n; i++) pow2[i] = pow2[i - 1] * 2 % p;
vector<ll> dp(k + 1, 1);
for(int i = 1; i < n; i++) {
vector<ll> binom(k + 1, 1);
for(int j = 1; j <= k; j++) binom[j] = binom[j - 1] * (pow2[i] + j - 2 + p) % p;
for(int j = 0; j <= k; j++) binom[j] = binom[j] * faci[j] % p;
vector<ll> nxt(k + 1);
for(int j = 0; j <= k; j++)
for(int x = 0; x < j and j + x <= k; x++)
nxt[j + x] = (nxt[j + x] + dp[j] * binom[x] % p) % p;
for(int j = 1; j <= k; j++)
nxt[j] = (nxt[j - 1] + nxt[j]) % p;
dp.swap(nxt);
}
cout << dp[k] * pow2[n - 1] % p << '\n';
}
}
2001E2 - Детерминированная куча (сложная версия)
idea & solution: Misuki
Fix the position of first and second leaf being popped, what's the property needed for $$$a$$$ to be determinitic?
Does the position of first leaf being popped really matters?
Fix the position of first leaf being popped, do we really need to consider all possible position of second leaf being popped?
Make good use of symmetry can reduce the complexity of problem significantly!
Make use of symmetry:
For convenience, let $$$\text{det_heap}()$$$ denote # twice-deterministic heap, $$$\text{det_heap}(v)$$$ denote # twice-deterministic heap where the first pop come from leaf $$$v$$$, $$$\text{det_heap}(v, u)$$$ denote # twice-deterministic heap where the first pop come from leaf $$$v$$$, second pop come from leaf $$$u$$$.
Similar to easier version, we have $$$\text{det_heap}() = 2^{n - 1}\cdot\text{det_heap}(2^{n - 1})$$$ because of symmetry.
Then consider enumerate $$$u$$$, the second leaf being popped, we have $$$\text{det_heap}(2^{n - 1}) = \sum\limits_{u = 2^{n - 1} + 1}^{2^n - 1}\text{det_heap}(2^{n - 1}, u)$$$
because of symmetry, again, for any $$$u_1 \neq u_2, LCA(2^{n - 1}, u_1) = LCA(2^{n - 1}, u_2)$$$, we have $$$\text{det_heap}(2^{n - 1}, u_1) = \text{det_heap}(2^{n - 1}, u_2)$$$, so for each LCA, we only need to enumerate leftmost leaf under it as second popped leaf and multiply answer with # leaves in such subtree.
Rephrase of Problem:
then consider the relation of values between vertices, we have
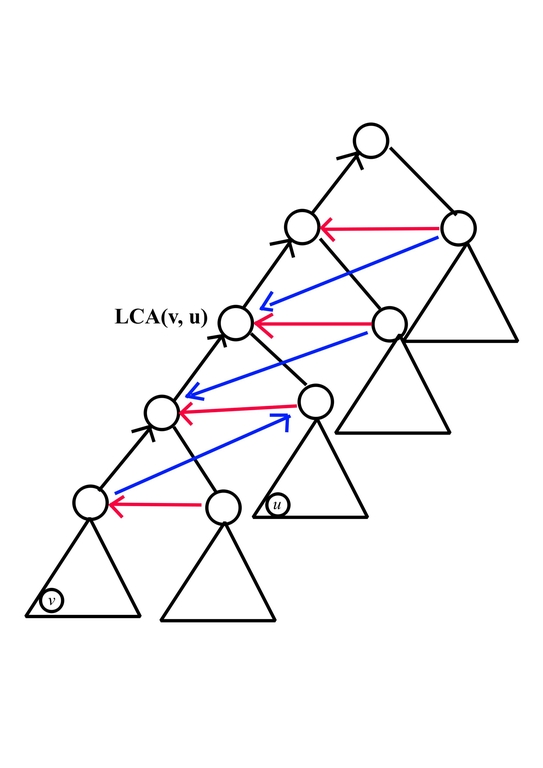
where
- black edge from $$$x$$$ to $$$y$$$ means $$$a_x \le a_y$$$, which comes from the nature of $$$\text{add}$$$ operation
- red edge from $$$x$$$ to $$$y$$$ means $$$a_x < a_y$$$, which come from the fact that $$$v$$$ should be first leaf being pulled
- blue edge from $$$x$$$ to $$$y$$$ means $$$a_x < a_y$$$, which come from the fact that $$$u$$$ should be second leaf being pulled
Eliminate Useless Conditions:
Then observe if we have some directed triangle consist of edges $$$(x, y), (y, z), (x, z)$$$, edge $$$(x, z)$$$ didn't bring extra relation so we can delete it, after that, we would have
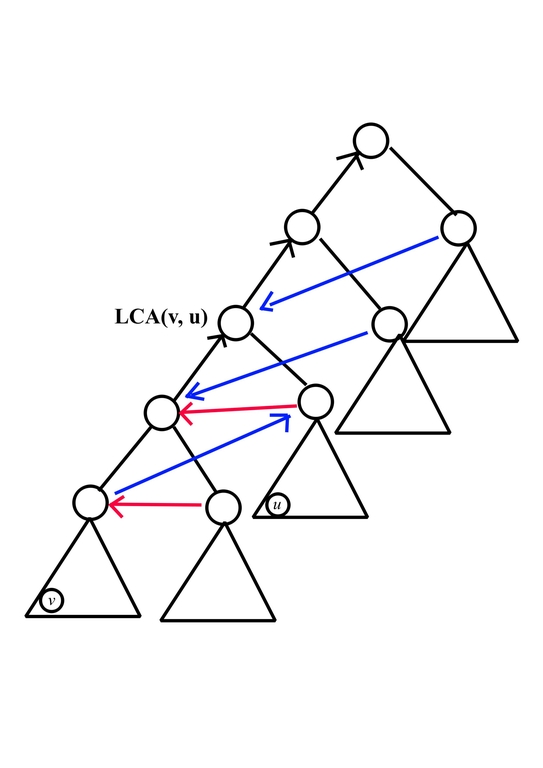
Applying Counting:
Then we can use pair of value of vertices from same depth as the state of dp, and enumerate such pair in increasing order of height while not breaking the relations, then we would have $$$dp[h][l][r]$$$ = # twice-deterministic heap when the left vertex have value $$$l$$$ and right vertex have value $$$r$$$ and the current height is $$$h$$$.
First, to handle the relation of Z shape formed by red/blue arrows and enumerate value of $$$(L, R, R')$$$, consider the following picture
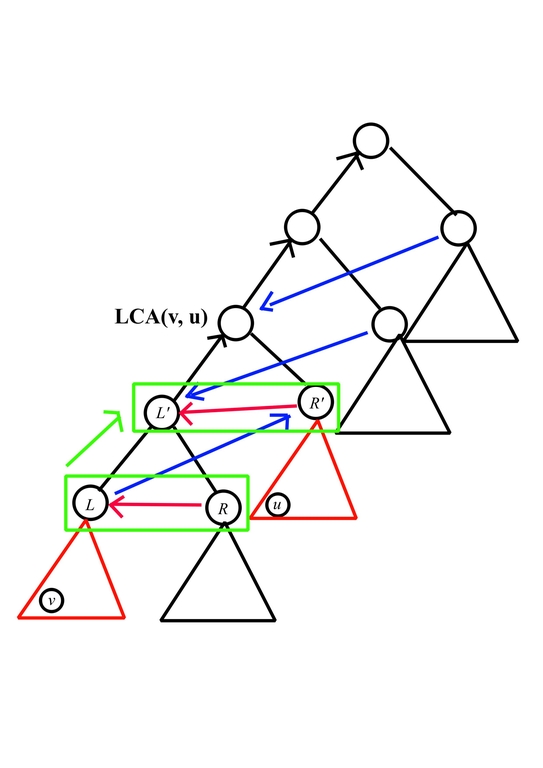
(The red subtree is one-time deterministic heap, while the other can be any heap.)
Also let $$$f(h, k)$$$ denote # deterministic heap for one time pop with height $$$h$$$ after doing operation $$$k$$$ times where the leftmost leaf being pulled, $$$g(h, k)$$$ denote # max heap with height $$$h$$$ after doing operation $$$k$$$ times (We already know how to compute them in easier version of this problem)
Let's fix the value $$$L$$$ and $$$R$$$, and push it to some $$$dp[h][L'][R']$$$, we need to satisfy
- $$$L' > R' > L > R$$$
- $$$L' \ge L + R$$$
in such case, enumerate all pair $$$(L, R), (L > R)$$$ and for all $$$L' \ge L + R, R' \ge L + 1$$$, add $$$f(h - 1, L) \cdot g(h - 1, R)$$$ to $$$dp[h][L'][R']$$$. After that, for every $$$L' \le R'$$$, eliminate its contribution, while for every $$$L' > R'$$$, multiply its contribution with $$$f(h, R') \cdot 2^h$$$. which can be done in $$$O(k^2)$$$ with the help of prefix sum.
Second, to handle the relation formed by black/blue edges and enumerate value $$$R'$$$, consider the following picture
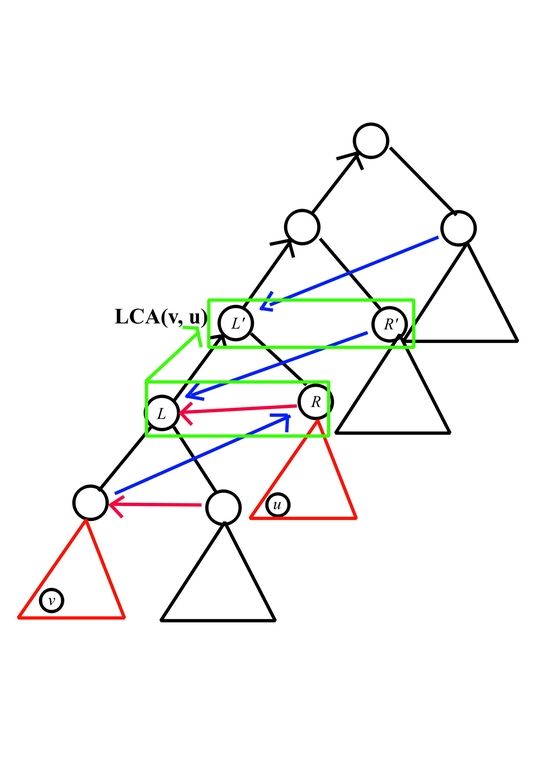
For each $$$L, R$$$, we need to push it some some $$$dp[h][L'][R']$$$ where the following conditions hold
- $$$L' \ge L > R'$$$
- $$$L' \ge L + R$$$
we can handle it by first adding $$$dp[h - 1][L][R]$$$ to $$$dp[L'][R']$$$ for all $$$L' \ge L + R, R' \le L - 1$$$. Then for all $$$L' \le R'$$$, eliminate its contribution, while for the other, multiply the contribution with $$$g(h, R')$$$, which can also be done by prefix sum in $$$O(k^2)$$$.
Then the answer would be $$$2^{n - 1} \cdot \sum\limits_{L + R \le k}dp[h - 2][L][R]$$$ and the problem has been solved in $$$O(nk^2)$$$.
#include <iostream>
#include <vector>
using namespace std;
using ll = long long;
int binpow(ll a, ll b, ll p) {
ll c = 1;
while(b) {
if (b & 1) c = c * a % p;
a = a * a % p, b >>= 1;
}
return c;
}
int main() {
int t; cin >> t;
while(t--) {
int n, k, p; cin >> n >> k >> p;
vector<ll> fac(k + 1, 1);
for(int i = 1; i <= k; i++) fac[i] = fac[i - 1] * i % p;
vector<ll> faci(k + 1);
faci[k] = binpow(fac[k], p - 2, p);
for(int i = k - 1; i >= 0; i--) faci[i] = faci[i + 1] * (i + 1) % p;
vector<ll> pow2(n + 1, 1);
for(int i = 1; i <= n; i++) pow2[i] = pow2[i - 1] * 2 % p;
vector<ll> dp(k + 1, 1);
vector dp2(k + 1, vector<ll>(k + 1));
for(int l = 0; l <= k; l++)
for(int r = 0; r < l; r++)
dp2[l][r] = 1;
for(int i = 1; i + 1 < n; i++) {
vector<ll> binom(k + 1, 1);
for(int j = 1; j <= k; j++) binom[j] = binom[j - 1] * (pow2[i] + j - 2 + p) % p;
for(int j = 0; j <= k; j++) binom[j] = binom[j] * faci[j] % p;
vector<ll> binom2(k + 1, 1);
for(int j = 1; j <= k; j++) binom2[j] = binom2[j - 1] * (pow2[i + 1] + j - 2 + p) % p;
for(int j = 0; j <= k; j++) binom2[j] = binom2[j] * faci[j] % p;
vector<ll> nxt(k + 1);
for(int j = 0; j <= k; j++)
for(int x = 0; x < j and j + x <= k; x++)
nxt[j + x] = (nxt[j + x] + dp[j] * binom[x] % p) % p;
for(int j = 1; j <= k; j++)
nxt[j] = (nxt[j - 1] + nxt[j]) % p;
vector nxt2(k + 1, vector<ll>(k + 1));
{
vector tmp(k + 1, vector<ll>(k + 1));
for(int l = 0; l < k; l++)
for(int r = 0; r < l and l + r <= k; r++)
tmp[l + r][l + 1] = (tmp[l + r][l + 1] + dp[l] * binom[r]) % p;
for(int l = 0; l <= k; l++)
for(int r = 1; r <= k; r++)
tmp[l][r] = (tmp[l][r] + tmp[l][r - 1]) % p;
for(int l = 1; l <= k; l++)
for(int r = 1; r <= k; r++)
tmp[l][r] = (tmp[l][r] + tmp[l - 1][r]) % p;
for(int l = 0; l <= k; l++)
for(int r = 0; r < l; r++)
nxt2[l][r] = (nxt2[l][r] + tmp[l][r] * nxt[r] % p * pow2[i]) % p;
}
{
vector tmp(k + 1, vector<ll>(k + 1));
for(int l = 1; l <= k; l++)
for(int r = 0; l + r <= k; r++)
tmp[l + r][l - 1] = (tmp[l + r][l - 1] + dp2[l][r]) % p;
for(int l = 0; l <= k; l++)
for(int r = k - 1; r >= 0; r--)
tmp[l][r] = (tmp[l][r] + tmp[l][r + 1]) % p;
for(int l = 1; l <= k; l++)
for(int r = 0; r <= k; r++)
tmp[l][r] = (tmp[l][r] + tmp[l - 1][r]) % p;
for(int l = 0; l <= k; l++)
for(int r = 0; r <= k; r++)
nxt2[l][r] = (nxt2[l][r] + tmp[l][r] * binom2[r]) % p;
}
dp.swap(nxt);
dp2.swap(nxt2);
}
ll ans = 0;
for(int l = 0; l <= k; l++)
for(int r = 0; l + r <= k; r++)
ans = (ans + dp2[l][r]) % p;
cout << ans * pow2[n - 1] % p << '\n';
}
}










Someone gotta explain C, cause solution above is unclear.
we can easily find if two nodes have edges or not using a divide & conquer approach. Lets say if we have two nodes $$$ x $$$ and $$$ y $$$. querying them will give us a node $$$ m $$$ such that m is the center of the distance. then we can solve it for $$$ (x, m) $$$ and $$$ (m, y) $$$ and so on until the answer of a query is either of the nodes.
The second big observation is that the root of tree is 1 so every node will be connected to 1 in some manner. so instead of applying divide & conquer between two random nodes, we can apply divide & conquer to 1 and any of the unvisited nodes yet.
Submission
You mean (x,m) and (m,y).
yes, my bad for the typo
Did they mention that the root is always 1?
any node can be the root in a tree. you can fix n to be your root node if you wish, it doesnt matter.
Any idea why I am getting RTE for same logic: https://mirror.codeforces.com/contest/2001/submission/277414456
Thank you for your excellent solution.
I tried the same way, can someone please help why it gives WA on Test 3. 280178005
For C there is a simpler solution with only n log n queries.
You can just "root" the tree in 1, and after that for each node, you'll determine is father. For each node $$$a$$$: $$$x_1$$$ = query(a,1)
$$$x_2$$$ = query(a,$$$x_1$$$) ...
$$$x_{l}$$$ = query(a,$$$x_{l-1}$$$)
When $$$x_{l}=a$$$ you stop and you know that the father of $$$a$$$ is $$$x_{l-1}$$$. $$$l<\lceil log(n)\rceil$$$ because each time you divide your path by 2. So at end it'll be n log n queries.
Hope I was clear.
Edit: Sniped above :)
Doesn't seem like a edit
Why can we root the tree at 1? Can't the root be any one of the nodes provided?
Since the edges are undirected, any node can become the root. Trying to draw a tree starting from any node at the zeroth level will help to understand this.
For instance, (1)-(2)-(3) can be (1)
|
(2)
|
(3)
or
(1)
/ \
(2) (3)
or
(3)
|
(2)
|
(1)
All these represent the same tree
Any vertex of the tree can be the root of a tree. So, the statement "the root can be any one of the nodes provided" is true. This means we can choose any node as the root and proceed with the process. Nodes 1, 2, ..., n are all valid choices. In this solution, we chose node 1 as the root, but selecting any other node would also be correct. (But please remember: you can only choose one node as the root in a solution. If you choose a different node, for example, node 3, then you need to consider nodes 1, 2, 4, 5, ..., n.)
consider a and b in a tree and distance between them is 7, so x would be some node in distance of 3 from a, and in distance of 4 from b, now you should change b to x (binary search) now you will give new x between a and new b, and distance between a and x is 1, distance between x and b is 2, that means you have an edge between a and x,
continue doing this approach for all node from 2 to n, you will find what is the parent of node i, and because we have a tree (we have n — 1 edges, that's why you should loop from 2 to n and not 1 to n), it works true.
you can see my code for better understanding,
hope it helps.
i couldn't accept it during the contest because my previous solution works in O(2*n*lon2(n)) and its more than 15*n.
Thanks for the super fast tutorial
I created video editorial for D: Longest Max Min Subsequence
I also created a practice contest with easy versions of problem D: https://mirror.codeforces.com/group/7Dn3ObOpau/contest/545195
Fast Tutorial
what can i say
i got ABSOLUTELY crushed. this contest made me rethink my life decisions and contemplate on quitting CP forever :(
gotta give props for the blazingly fast editorial though
Keep going, I had thought about that, but it is very satisfying to see your improvement over time
Well, I still try to go on even after 44 unsuccessful contests. :( Maybe, you can draw some inspiration from me and ...
"quit early! :P
Just kidding!!
I don't think I understood B, can someone please explain why for n == 4, 3 1 4 2 isn't valid? I thought that you could build on this for even n, making n==2 the only impossible input.
Forwards takes 2 passes, backwards takes 3.
a = [3, 1, 4, 2]
The typewriter 1 will go 1 and carriage return once, then go to 2 and carriage return twice and go to 3 and then to 4
So the carriage return total of typewriter 1 is 2
Now let's consider typewriter 2, typewriter 2 will go to 1 and carriage return then go to 2 and to 3 and carriage return twice and then go to 4
Both of them take 2 carriage return so it should be valid rigtht?
Typewriter 1 can go from 1 to 2 without returning in between.
"The typewriter 1 will go 1 and carriage return once, then go to 2 and carriage return twice and go to 3 and then to 4"
It is possible for typewriter A to collect 1 and 2 without returning. Since we are looking to minimize the carriage return operation, the optimal number would be 2.
if we consider minimum carriage returns in your permutation typewriter1 needs 2 returns and typewriter2 needs 3.
from the pointer facing at 1, to generate 3 1 4 2, you could do 1 2 in one traversal and then return and do 3 4 in 1 traversal. So 1 return in total.
but from the pointer facing at n, to generate 3 1 4 2, you first need to get to third poositing and make it 1 then return, then traverse to make 2 and 3 and return again and then make 4 (since 4 comes before 3 that way) so you made 2 returns in that way. Minimum of 2 isnt equal.
for left typewriter it will be 1 return pass as 1 2 return 3 4, but for right typewriter it will be 2 return pass as 1 return 2 3 return 4.
Super-fast editorial!!!
We can do binary search on trees ?!?!
Well we can use divide and conquer
this contest gave me the encourage to quit CP
Could someone tell me the prbleam about my code? ~~~~~~~~~~ //this is my code from sys import stdout def ss(x,y): if x!=y and b[x][y]==0: print('?',x,y) stdout.flush() z=int(input()) b[x][y]=z if x==z: a.append(x) a.append(y) else: if x<z: ss(x,z) else: ss(z,x) if z<y: ss(z,y) else: ss(y,z) for _ in range(int(input())): n=int(input()) a=[] b=[[0 for i in range(n+1)] for i in range(n+1)] for i in range(1,n): for j in range(i+1,n+1): if b[i][j]==0: ss(i,j) print('!',*a)
~~~~~~~~~~
this is C
Could you please put it in a code block for easier visualization?
Please use collapse/spoilers the comments are getting quite messy and lengthy.
E1 can be solved in a much simpler way (277414233) without any binomial coefficients or combinatorics.
D can be solve in O(n).
Firstly we make a frequencie array to count every element how many times it repeated.
Then we make an empty vector to store ans in it, to store answer we will walk through the elements as the input give is, we do mp[a[i]]--,if the element already in ans we continue , if not we push it in best place we can , I mean by that we keep pop back until we put it in best place but we can popback if the back element counter is it's greater than 0, and when poping it we are sure that it's the best move by some condtions.
277423267
D was pretty nice, I wish I actually knew trees, so I could attempt C as well. I think I'm gonna reach expert regardless though! very nice contest, thank you!
B was easy, If we can understand the problem and write some testcases
In most of such problems , I end up not understanding but today I did B
SUPER FAST!Thank You!
The Problem is funny.I love this round!
general idea is really useful.
Thanks.
Btw, problem D is nice
Another approach to solving problem C is to assume that the tree is rooted at vertex $$$1$$$. For each vertex $$$u = 2, 3, \ldots, n$$$, the goal is to find its parent $$$p(u)$$$.
By using the function $$$\texttt{query}(u, 1)$$$, you can get the midpoint of the path from $$$u$$$ to its ancestor $$$1$$$. Keep halving the path until $$$\texttt{query}(u, x) = u$$$, which means that $$$x$$$ must be $$$p(u)$$$. This method will find $$$p(u)$$$ in no more than $$$\lceil \log_2 (n-1) \rceil$$$ queries!
thanks your easy answer
I like that General idea,it really help me much!!!
glad you like it :)
I am sorry to bother you ,but can you tell me the General idea of promlem C
I am confused about the Solution.I cant find out the index logic.
It have less standard idea and rely on pure puzzle solving ability more in my opinion, but if you have a good perspectice about the problem it might be easier. For example, I think the problem as some kind of spanning tree problem and try to keep finding edge connect different component. (Solution2 in editorial)
I cant understand problem C .How the binary work? Why use the binary search?
Sorry, I was thinking hint for my solution when writing it but the solution part is from coordinator. I've add Soluion2 which correspond to the hint section.
Maybe I'm misreading the solution to C, but I think this is simpler. The key idea is that $$$(u, v)$$$ is an edge if and only if querying
? u vreturns $$$u$$$. Then, for each $$$2\le v\le n$$$, we can query? v 1, take the result $$$x$$$ to query? v x, etc, until we reach some node $$$u$$$ with? v ubeing $$$v$$$.In this way, you can think of this as rooting the tree at node $$$1$$$ and discovering the parent of node $$$v$$$ for each $$$v\neq 1$$$ in this rooted tree, which must by definition give $$$n - 1$$$ distinct edges.
Edit: Sniped above :)
It seems I have an alt approach for C.
Ask $$$(1,u)$$$ and $$$(u,1)$$$ for all $$$u$$$. Then, try to find $$$d(1,u)$$$.
Of course $$$d(1,1)=0$$$, and if $$$(1,u)$$$ returns $$$1$$$, $$$d(1,u)=1$$$.
Now we can restore $$$d(1,u)$$$ for all $$$u$$$.
$$$d(u,v)$$$ answers the midpoint of $$$u$$$ and $$$v$$$ (if $$$d(u,v)$$$ is odd it answers the nearest one to $$$u$$$).
Because of this, for all $$$u$$$, if $$$(1,u)$$$ returns $$$x$$$ and $$$(u,1)$$$ returns $$$y$$$, $$$d(1,u) = d(1,x) + d(1,y)$$$ is always satisfied. From the information on step 1-1, we can found all of $$$d(1,u)$$$ in a chain.
For all $$$u$$$, begin with $$$x=1$$$, repeat $$$x \leftarrow (u,x)$$$ until $$$d(1,x)+1 = d(1,u)$$$. Now, if the tree is rooted at $$$1$$$, the parent of $$$u$$$ is $$$x$$$.
277363292
Now I notice step 1 isn't needed (we can avoid the step with modifying step 2). Why?
Let's define an array $$$\text{parent}[i]$$$, initially for all $$$2 \le i \le n$$$ set $$$\text{parent}[i] = query(1, i)$$$.
Initially let node $$$1$$$ be taken and all other nodes not taken. Repeat until all nodes are taken: find any node such $$$i$$$ that $$$\text{parent}[i]$$$ is taken and ask $$$query(\text{parent}[i], i)$$$. If the result is $$$\text{parent}[i]$$$, then $$$i$$$ and $$$\text{parent}[i]$$$ are connected by an edge, so add it to the answer and set $$$i$$$ to be taken. Otherwise, set $$$\text{parent}[i]$$$ = $$$query(\text{parent}[i], i)$$$.
This works because every time we do not take a node $$$i$$$, the distance between that $$$i$$$ and $$$\text{parent}[i]$$$ halves, so for any node we only need to process it $$$log_2(n)$$$ times. I find this solution more intuitive than the editorial one personally.
Edit: seems like a few other people posted the same solution while I was typing it, lol
For C I did the following. Initialize a stack of pairs with all
(i, j)wherei < j. While the stack is empty, I pop(a, b). I check using a DSU ifaandbbelong to the same connected component (that has been discovered till now, and skip if they do. If they don't, then I query? a band push the outputxto the stack ifx != a. Otherwise, I push the found edge and merge the two components.I think this should always find all edges while remaining under the query limit. But I don't understand why this WAs. Could someone explain?
277403335
For C, I used DFS and it seems to have worked somehow. Could someone explain it?
277409228
Do anyone know a software that have a faster execution for interactive problem?
I use jdoodles but it not stable
I was unsure before submitting the code for problem C but it passed the pretests.
Problem D is nice idea but it's hard implementation!
Solution D in O(n) (attempt: 277409175)
We will store the current response in the ans array. Initially, ans is empty.
Let's build an array r, where r[x] is the maximum index i, such that c[i] = x
Let's build an array of used, where used[x] = True if the value of x is contained in ans and False otherwise. Initially, all values are False
Let's go through the c array.
Let's consider the value of c[i], if used[c[i]] = True, go ahead, otherwise we will execute the next cycle:
If ans is empty, we do nothing and exit the loop
If r[ans.back()] <= i, exit the loop
1) If ans.size() % 2 == 0, then
1.1) If c[i] < ans.back(), then delete the value of ans.back(), do not forget to put the corresponding value to the array used (used[ans.back()] = False) and return to the beginning of the cycle
1.2) Otherwise (if c[i] > ans.back()), check
1.2.1) If c[i] > ans[-2] (the penultimate element in ans), then remove the last two elements from ans, do not forget to change used, return to the beginning of the cycle
1.2.2) Otherwise (if c[i] < ans[-2]), exit the loop
2) Otherwise (if ans.size() % 2 == 1) we perform actions similar to 1), but change the signs to the opposite ones (> to <, and vice versa) After the loop, add c[i] to ans, do not forget to change used (used[c[i]] = True)
When we go through the entire c array, the ans array will be the optimal answer.
Since we add and remove each element from ans once, the asymptotics is O(n)
Reading question B reminds me of how research papers are written ;))
The problems were enjoyable, but Problem B lacked clarity. In future contests, it would be great to see more emphasis on covering more cases for such problems.
What topics should I learn to solve problem D?
greedy, implementation, sorting , optional -> (priority queue), set
I spent all my time trying to solve it with DP, segment tree.... (some advanced stuff) and now It's just greedy and implementation :(
same here
you can use segment tree
Well, it can be done using segtree
277435255
277445159 can you please help me what am i doing wrong here ?
can be done via segtrees
https://mirror.codeforces.com/contest/2001/submission/277440499
same
Don't overestimate the problem I thought about DP, but the constraint clearly will not help.
I thought about segment but i feel like the problem I would struggle with segment could be easily solved by a frequency array
C does not use binary search as mentioned in the editorial, but some version of binary lifting
Sorry, I've add binary search solution on it (Solution2)
Good quality contest, thank you !
for B we can just say if n even then not possible and if odd
we can construct like this--
for 3 -->1 3 2 for 5 -->1 3 5 4 2
for 7 -->1 3 5 7 6 4 2
and so on
A super simple way to solve C:
Please use collapse/spoilers the comments are getting quite messy and lengthy.
sry, my bad.
Awesome work! Love those general ideas!
D can be done with simple stack
First though of dp ,then greedy approach striked but wasnt able to implement it.
Can someone please help me figure out what is wrong in my soln to D link
In this:
I have a turn variable which tells us that we have to maximize or minimize the next element to be chosen.
A variable lst that keeps the last printed index.
A set st that keeps track of the elements that can be selected in future with their indices.
A map that keeps the count of elements that are left in the array and are not visited till now.
Take a look at Ticket 17476 from CF Stress for a counter example.
Thank you so much
Does anyone have test cases for D? Looks like I'm failing somewhere on Test 3.
I figured some out for my submission
Here's one that I failed on:
Answer should be:
An even simpler one I failed on:
Answer should be
off-topic but quick question: why is my activity section different for everyone except me? i see a 15 day streak when logged in while in incognito mode i see an 11 day streak, is this normal?
i think it shows it on your local time when you're not incognito, but when you use incognito, your local time defaults to whatever incognito is set to be. so for some time zones you didn't actually keep your streak.
man i was trying making a 90 day streak, sad :(
gotta start again now
i wouldnt say you have to start again, youre bound to lose the streak on some timezones that are far from yours. good job on the streak so far though, i hope you'll reach your goal
thanks, looks like you just turned expert too. congratulations!
Wasn't able to completed problem D during contest but I liked it.
And the general idea section is super useful.
Can someone please tell me what i did wrong in the 3rd question
https://mirror.codeforces.com/contest/2001/submission/277397815
It's been 1.5 hours and i have read many other solutions and even the official one, and i do not understand where my logic went wrong.
thanks
it looks like you did not flush after each output.
I thought endl automatically flushes everything
Dear tester, Kind request, when you write program to match the contestant's output, with correct output, Please give some meaningful errors, which can help the user in debugging the issue.
wrong answer 3919th numbers differ — expected: '1', found: '3'
How am I supposed to know, 3919th number is from which test case ????
It would have been great help, if you had simply put here the test case number, I could have used some tricks to find out where my solution is failing :| .
cc: Misuki
This have nothing to do with the testers, this is built in checker which compare author solution output and your output, and this is the default output when your output differs.
cool . no issues.
Actually I would recommend you to write a bruteforce and see where goes wrong with your solution. Since in contest, you can't see the hidden testcase, and it's useful to have such ability as a contestant.
sure, will adapt. <3
Take a look at Ticket 17477 from CF Stress for a counter example.
I found the error buddy. Just changing
>to>=fixed my code, and got AC.WRONG SUBMISSION : https://mirror.codeforces.com/contest/2001/submission/277418236
RIGHT SUBMISSION: https://mirror.codeforces.com/contest/2001/submission/277433853
You can put a counter, set it to zero once it reaches 3919 print that test case. (you should only apply after you tried enough to find the mistake by yourself)
What is the difference between Code and Code 2 for the C problem? I tried and was not able to find the difference :(
Both look exactly the same. I mean Letter by Letter.
when i trying to hack this submission, it shows "Unexpected verdict".
here is gen:
It seems that some code that should be TLE is incorrectly tagger correctness in polygon, please check this.
upd. physics0523 seems facing same question?
Maybe some intended solution on Polygon also gets hacked or validator is broken or something
Turns out a tester's solution TLE on the hacked test, now it should be fixed.
Let's share my generator:
Some false (and maybe too straight-forward simulation) solutions takes $$$O(N^2)$$$ in this case.
Am i missing something in D?
Here is what i did (ITS WRONG and idk y):
3 arrs:
Original and a Boolean array for the user input, (i think if we use this then we can edit and delete members from our sub array in O(1) time)
Another third array digits, which stores each digits index position, essentially this array stores the place where we picked that digit from (-1 if we didn't pick it up at all)
as we iterate over the original array, a[i], we check if digit [a[i]] == -1, if it is update digit[...] = i. (this ensures that we always pick the largest sub seq, also we toggle the boolA[i] = true)
now the other possibility is that if digit[...] != -1, this means that we did pick it up before.
If we picked it up, we check the original's location:
if it is odd, this means that we want to keep it as large as possible and hence we will only remove (and hence append) if it is smaller than the next element we have chosen.
if it is even you do the same for minimum. finally after one iteration you have the largest sub seq.
this gave me wrong answer on pretest-2 meaning that it isn't the correct logic, i just want to know why
Thanks for the general ideas, hints, and fast editorial. Really appreciate it!!
I Think in problem D it is more intuitive to think about storing range min and max in a segment tree and once an element is taken update min value to 1e9 and max value to -1e9.
Agreed, segtree was easier to think in this question.
My solution-https://mirror.codeforces.com/contest/2001/submission/277423515 I have used 2 segment trees, it can be implemented in the same tree using a structure to store min and max or as a pair.
I still can't figure out why my submission to C is incorrect and giving wrong ans. Somebody please help ,my implementation is clean
My submission
Found it! I was randomly printing the ans at the end , didnt see that we have to print serial wise 1..n-1
For A , the hint encourages us to think about the lower bound of the answer . For me it is 0 (the case where all the elements in the array are equal ) , and that doesn't help in any way . What did the author expected as an answer when they gave us this hint ?
I know this is a very silly question perhaps even meaningless but any help is appreciated
I mean the lower bound of the answer for any fixed $$$a$$$, not necessarily with all elements equal
I am new to interactive problems. My solutions got idleness limit exceeded. It is mentioned in the statement that this happens when you don't flush the output put I do. Can someone suggest what would be the problem?
If you are using c++. then please refer to this.
#define IOFLUSH fflush(stdin);fflush(stdout);Whenever you take input, or print any output. just write this statement before and after it, to avoid any sort of issues.
IOFLUSHThis should solve the issue.
I would use cout<<flush or cout.flush() instead of fflush(stdout); the latter only flushes cout if you didn't set ios::sync_with_stdio(0), because stdout and cout are not the same thing (I'm assuming you use cin and cout for I/O). I'm also pretty sure flush(stdin) doesn't do anything, but I could be wrong about that.
I got a bit confused now. If I am setting isos::sync_with_stdio(0) I should use cout << flush; or cout.flush(); ? another question doesn't cout << endl; do the work? I think after the contest when I upsolved the question I just used cout << endl; only
cout<<flush and cout.flush() do the exact same thing, so it doesn't matter. As for cout<<endl, it flushes and outputs a newline at the same time, which is often desirable and it can be the only way your code flushes, but writing something like cout << answer << '\n'; cout << endl gives you an extra newline (though I'm not sure if that actually matters). So if you want to define something like IOFLUSH to use in the way comment above says, using cout<<endl would be weird and possibly wrong, but for flushing one line, it's perfectly fine to just write cout<<endl instead of cout<<'\n' whenever printing a newline.
ok I undrsyood it, thak you bro
Can someone hack my solution for problem D 277416865. The complexity is O(nlog²) and I think the worst case is :
n , 1 , n-1 , 2 , n-3 , 4 , n-4 , 5....
Can someone explain me B? I don't think I can understand the task properly(maybe cuz im dumb ;() but why can't i just go forward without returning on bot typewriters, or maybe thats not how pointer works?
The problem states that, in a move operation:
Hence, after moving to the last position, the pointer must return to its initial position to be able to write again.
The way I understand this problem, a valid permutation should have the same number of inversions of consecutive numbers, going from left to right and from right to left. One way to achieve such a permutation is to start at the middle index and go back-and-forth in the array until it goes out of bounds (or vice-versa).
277352967
Can anyone help me find error in my code? I'm trying to solve D and it is giving wrong answer on test case 3. Here is my submission: https://mirror.codeforces.com/contest/2001/submission/277428182
Take a look at Ticket 17479 from CF Stress for a counter example.
Can anyone find my error in problem C? This is my submission 277387198, which should be quite self explanatory. I tried to find the edges on the path $$$1---u$$$ for all undiscovered node $$$u$$$ by querying $$$(1,u)$$$. If it returns $$$x$$$, query $$$(1,x)$$$ and $$$(x, u)$$$. Skip the query $$$(1,x)$$$ if x is already discovered.
The solution looks ok to me, and I got a verdict saying WA on test $$$5$$$, but seems like test $$$5$$$ is a tree with edges $$$1-2,1-3,1-4$$$ which my solution can detect. Any help with the solution or a test case that fails will be helpful. Thanks.
This looks so inefficient. I think getNew(int n) can return 1, running resolve(1,1) will add edge(1,1), which is incorrect.
My similar solution https://mirror.codeforces.com/contest/2001/submission/277595574
I solve problem D using Lazy segment tree. My solution: 277441928
I hope it is helpful.
Problem D didn't have strong enough test cases a O(n^2) approach gets ac in main test, the triggering worst case test would have been n/2 1 n/2-1 2........ repeated twice.
Came here to say that.
Sorry about that, I didn't notice such bruteforce solution during preparation, I would take more care about such thing next time :(
I am not able to understand the last paragraph of the Editorial for Problem D. Can someone explain it in detail? Also How to solve it using segment trees?
Hey,can you help me with C my solution,I used something similar to the editorial but it exceeds 15n queries however for any numbers of node it can only go upto 2^(ceil(log2(n))+1) operations. Code:277462404
In question D ,Accepted solutions of the contest are judged till only 30 test cases while judging is now taking place on more test cases. Matter of surprise is that many accepted solutions are now giving Time limit exceeded on test cases after 30.
D similar to https://open.kattis.com/problems/earlyorders
Can anybody tell me why my code gives wrong answer on test case 3 for problem C
code link: https://mirror.codeforces.com/contest/2001/submission/277440400
problem C : code for solution 1 is the same as solution 2
can someone explain d&c wtih dsu solution in problem C
My solution with divide and conquer: Submission #277404397
Why the maximum query count does not exceed 15n?
I am confuse about problem B, maybe I am wrong, I thought for all odd case, I just need to swap(a[0],a[n//2]), for example: [3,2,1,4,5] -- > type 1: 1 -->2-->3,4,5; type 2: 1,2,3 -->4-->5
In Problem C I was getting idleness limit exceeded on testcase 2 but when i corrected the logic of the code the error was gone..so i wanted to ask that can idleness limit exceeded error occur also when your code's logic wrong?
I always get hints for problems rated high like D but don't know why I didn't able to solve the problems
Both codes for C are the same...
Sorry, it should be fixed now.
Thank you for the fast editorial and I love the General idea sections.
where did the binomial coef come from in problem E1
edit : i think i get it using the stars and bars method we can move the size — 1 to a next node or increase the value at the current node till the root
For anyone else wondering about where the binomial coefficients come from, here's an alternate explanation.
Let's try to find the number of unique max heaps using the $$$k$$$ operations without worrying about the deterministic conditions. We start with a max heap (since all elements are zero), and doing an operation maintains the max heap invariant. So, we only have to blindly apply the operation on nodes.
Let $$$T = 2^{n} - 1$$$
The first thought that comes to mind is to perform the first operation on a random node, and then recurse for the same tree, with $$$k - 1$$$ ops left, i.e, something like
$$$f(k) = T\cdot f(k - 1)$$$
However, this leads to overcounting. Consider
Notice that if $$$k = 2$$$, these configurations are essentially the same. Hence, we can deduce that round number at which a particular node participated is not important, what's important is how many rounds did it participate in.
So, let's call the number of participation rounds for each node as $$$x_1, x_2 \dots x_T$$$, then, since there can only be $$$k$$$ different rounds, we should have
$$$x_1 + x_2 + \dots x_T = k$$$
So the number of unique max heaps is the non-negative integral solution for this equation, which is pretty well known via Stars and Bars to be $$$k + T - 1 \choose k$$$
Could you explain the transitions for E1 in greater detail? I've been stuck trying to understand how the previous states are used to compute the next ones.
First, let's find out the number of unique max heaps using the $$$k$$$ operations (Let's disregard deterministic properties).
$$$dp[n][k]$$$ represents the number of unique max heaps on $$$n$$$ levels perfect binary tree with $$$k$$$ operations. Then, let's think about how many operations will we use at the root, $$$root \in [0, k]$$$, and the remaining number of operations is $$$remain = k - root$$$.
Then, from the remaining number of operations, we need to distribute some operations to the left and right subtree. How many operations can left receive? $$$left \in [0, remain]$$$, Therefore, $$$right = remain - left$$$. After distributing the operations, the left and right subtree have become independent. Hence, the transitions are:
Note that $$$dp[n][k]$$$ is $$$T + k - 1 \choose k$$$, as described in my earlier comment, but I just showed you a DP instead of a combinatorics approach.
Now, how do we count unique deterministic max heaps? The first thought that comes to mind is to track the final value of each node, something like $$$dp[n][k][val]$$$. However, if you think about it, this value parameter can be inferred from other parameters. The root will always have $$$val = k$$$.
Then, you might think about blocking the transitions when $$$left = right$$$. However, that is also incorrect, because left and right child are allowed to be equal if the node is not on the path defined in the problem. This means that we need to track another DP parameter, which would be a boolean.
$$$dp[n][k][on\_path]$$$ is no. of unique max heaps on $$$n$$$ levels with $$$k$$$ operations such that $$$on\_path$$$ denotes whether root is on the path.
But since 3D DP will be hard to visualize and optimize, let's remove the boolean parameter, and maintain two 2D DP. Define $$$indp[n][k]$$$ to be the number of unique deterministic max heaps when the root is in the defined path. Similarly, define $$$outdp[n][k]$$$ to the number of such configurations when root is not on the path.
To perform the transitions,
If $$$left > right$$$
But if $$$left < right$$$
There are $$$O(N \cdot K)$$$ states and transitions are $$$O(K^2)$$$. Hence, the time complexity is $$$O(N \cdot K^3)$$$.
How to optimize it? Before we do that, let's consider the problem of finding the sum of pairwise product in an array
You immediately know a 1D DP approach. But can you optimize this 2D DP. Why or why not?
Optimization is not possible, because when a gap is fixed, there is no pattern, or any number that remains constant. However, we didn't really need to fix the gap, we could've fixed $$$a[i]$$$ and inferred all the possible gaps, and come up with $$$a[i]*suffix\_sum$$$.
We will use the same trick here. Instead of fixing $$$root$$$ and then iterating through $$$left$$$, let's directly iterate through $$$left$$$ and notice its contribution. You'll realize that $$$indp$$$ only takes contribution from a subarray sum of the previous row of $$$outdp$$$. Hence, you can optimize using prefix sums.
The time complexity is now $$$O(N \cdot K^2)$$$.
Code
Hey, thanks a lot for the quick reply and detailed explanation! I think I understand your solution, though I think there's a small typo where outdp[n — 1][k] is supposed to be outdp[n-1][left]. Would you also be able to explain the DP transition in the editorial solution?
It's the same as the transitions in my DP, except it does the heavy lifting through combinatorics (which isn't really required, it can be offloaded to DP).
Notice that my $$$outdp[n][k] = {n + T - 1 \choose k}$$$. (We can see from combinatorics above, but we also chose to calculate it using DP. Let's call it as $$$f(n, k)$$$ from now on.
If you don't want to compute it explicitly, just remove the $$$outdp$$$ matrix altogether. Then, you'll notice that the $$$dp[n][k]$$$ in editorial's solution is same as my $$$indp[n][k]$$$. Then, take my old transitions,
and let's remove all keywords that reference $$$outdp$$$ and use the combinatorics equivalent.
The editorial's transitions are written in a fancy way using $$$x \in [0, j)$$$ $$$l \in [j + x, k]$$$ But my transitions with left and right are doing the same thing, except I use Receiving DP while editorial uses Distributing DP.
If you want to visualize how trees are computed using editorial's, you can just visualize how trees are computed using left and right variables above, and apply the same thing there. The crucial idea here is that since you are calculating indp, one of the child would go to outdp, and one would remain for indp, hence that's why you see the product of binomial coefficients with DP. If you understand the above DP, you should be able to understand editorial's DP as well. Let me know if anything specific that you're confused about.
Yup, that makes a lot of sense now. Thanks a lot!
can anyone help me figure out why this solution is failing? I have tried a few different things but Im stuck and can’t seem to find the problem 277468507
Hi, what might have gone wrong here? (Problem C)
-Thank you!
Stuck with problem D still.
I get it that we wanted to greedily build the sequence by picking the best element within the set of element with the right number of distinct values goes after it,
What baffles me is that this is a changing quantity. Let's say the test case is
we can easily construct cnt (cnt is the number of distinct values goes on or after it)
At this point it is fairly obvious that we should choose 5 so that -5 is lexicographically smallest, but then the
cntchanges toThe change is that everything before the last occurrence of the removed element has to have their cnt subtracted by 1.
I don't understand how can we solve this with a priority queue (or a bunch of them).
Video editorial for D
You count array changes in each iteration, yes. But there's a smart way to do a lazy update of this count array in amortized $$$O(n)$$$.
You have already deduced that something strange happens when an element appears for the last time. So, let's mark all such indices in RED. We will mark all the other indices as green.
arr: [5, 4, 2, 1, 3, 5, 2, 1]
col: [G, R, G, G, R, R, R, R]
It's easy to see that the size of the answer is equal to the number of red indices. What more can you infer? Consider the first red index. Every green index to the left of it will have the maximum number of distinct elements to the right. Hence, all of them are possible candidates for the 1st element. However, notice that since this is the first red index, this is your last chance to take one copy of the element that it's representing. So you need to greedily construct subsequence from the prefix ending at red such that the value of the final element selected is equal to the value of the red element.
So, suppose you take 5, of course, the count array changes, but the color array gives you the required info to track this change. Specifically, all elements between the last chosen element and the second occurrence of the red index would have the maximum number of distinct elements to the right that is possible and they are the only possible candidates for the second element. (Why? Because if you go past the second red index without taking it, you will lose one element forever).
The crucial idea here is to notice that it's a hard task to update each element in the count array, so we instead focus only on the updated values of the possible candidates, and we also don't need to keep track of the number of distinct elements to the right, we only care about candidates that have the maximal number of distinct elements to the right which are not yet taken. And this can be easily maintained by that color array I showed you.
Code implementing this idea
Thanks, with your help, I finally get this accepted.
I hope the code is clear — it is basically your idea by only keeping the valid candidates, no need to worry about the number of distinct elements of any other invalid ones.
I think I might be able to simplify it a lot more if I delete the element more lazily, having to implement a priority queue that support deletion seems too much for a contest problem.
Sir, come to C++. We have priority queue that supports deletion :)
set
Yay, it worked.
This is some text. I don't understand why I exceed time limit in problem B.Can someone please tell me?
The rest of the text. close
Help needed in my C solution, according to the code as far as I can think my solution should have asked <15n queries but it isn't and is failing.someone please have a look,it's idea is somewhat similar to the editorial. Code:277462404
Here's an $$$O(n)$$$ stack solution for D.
277484094
The problem is very similar to the LeetCode problem 1081. Smallest Subsequence of Distinct Characters but this time we have two stacks, one for the even indices and odd ones.
Then, when checking to pop and replace an element in one of the stacks, we can only do so if both stacks' top elements appear later on in the sequence.$$$^{\star}$$$
There was a bit of annoying casework on the lengths of the stacks (the max stack length is always $$$\geqslant$$$ the min stack length) to get it all to work.
$$$^{\star}$$$ slightly oversimplified, if both stack sizes are equal and we wish to replace the min stack's top, we don't need to check the max stack's top since it for sure comes before the min stack's top. The max stack case is handled similarly.
I also solved that LeetCode problem before and noticed that it's very similar (unfortunately I didn't look at D during the contest because of C), but for some reason my implementation is getting "wrong answer 119167th numbers differ" on test 4, not sure if anyone had a similar problem
Take a look at Ticket 17481 from CF Stress for a counter example.
Thank you very much, found the issue very quickly from there — I didn't skip the value if it's already in the stack.
No general idea given for C, here's my suggestion: Usually half/middle indicates binary search applies to the problem.
Please continue this General idea thing for the upcoming contests on codeforces, they are really useful.
how does the calculation of NCR(x+2^i−2,x) work for E1? how to find (x+2^i-2)! %p or (2^i-2)! %p when i is up to 500?
We can write C(x+sz-1,x) = fact[x+sz-1] * ifact[x] * ifact[sz-1] = sz*(sz+1)...*(sz+x-1) * ifact[x]
sz can be up to 2^500??
Ya but we only need sz%p which can be calculated using binary exponentiation
I just tried to understand the formula and it made much more sense now. Thanks!
Finally solved C after 10 wrong submissions!
congrats
I could not understand the problem C.
Misuki
I think in E2, the first condition of the last picture's transition (the second case in counting) needs to be:
$$$L' > L > R'$$$ and $$$L' > L > R$$$
Thanks you, I've fix it. the second one is $$$L' \ge L + R$$$ because the nature of the operation (i.e. whenever you add $$$1$$$ to a node, you would also add $$$1$$$ to its ancestors)
My solution for C:
https://mirror.codeforces.com/contest/2001/submission/277413728
Idea: root the tree at 1, find the path from all nodes to 1. Mark all nodes that have found the path to 1. Let c = query(a,b), if c==a then there is a is connected to b; else recursively query(a,c) and query(c,b), then mark a and mark b. If a and b having already been marked, that mean we already found the path from 1 to a and from 1 to b, there are already a path from a to b, so we don't need to find again.
277619651
this is my submission for D. Can anybody help in finding the issue.
My approach is very similiar to that of the editorial. I iterate over the pairs (last index of x, x), and maintain a multiset of elements of "a" between any two pairs, greedily picking max or min. (WA on tc3)
Take a look at Ticket 17483 from CF Stress for a counter example.
Thanks a lot
can anybody tells me if there are any problems?wa3,i am really sick of it ~~~~~ int ask(int x, int y) { cout << '?' << ' ' << x << ' ' << y << endl; cout.flush(); int res; cin >> res; return res; }
void dfs(int x, int y) { if (x == y)return; if (mp[{x, y}])return; mp[{x, y}] = 1; int ans = ask(x, y); if (ans == -1) { return; } if (ans == x || ans == y) { res.push_back({ x,y }); } else { dfs(x, ans); dfs(ans, y); } return; }
void solve() { mp.clear(); int n; cin >> n; for (int i = 2; i <= n; i++) { dfs(1, i); } cout.flush(); cout << '!' << ' '; for (auto item : res)cout << item.first << ' ' << item.second << ' '; cout << endl; mp.clear(); res.clear(); }
~~~~~
How to efficiently calculate combinatorics in E1? I thought it takes 2^i operations to calculate
You will see we can calculate it with $$$O(X)$$$ if you see submissions or official code.
D is a tough problem but Shayan implementation is so clean and easy to understand! Thank you for your video tutorial!
Can someone help with this submission failure for problem D?
3rd test case is failing:
wrong answer 7289th numbers differ - expected: '1', found: '2'https://mirror.codeforces.com/contest/2001/submission/277681400
Take a look at Ticket 17485 from CF Stress for a counter example.
My solution for D gives me tle, but I don't think I should get tle
277711569
Help Needed with Problem D : Longest Max Min Subsequence (Codeforces Round 967 Div. 2)
Hi everyone,
I'm currently working on Problem D : Longest Max Min Subsequence from Codeforces Round 967 (Div. 2). You can find the problem here (https://mirror.codeforces.com/contest/2001/problem/D?mobile=true ).
I've been stuck with a "Wrong Answer" on test 4. You can check out my submission here(https://mirror.codeforces.com/contest/2001/submission/277854508).
The checker log says that the 79924th number is different than expected, with my code outputting '4' instead of the expected '3'. Would appreciate If someone could point out the bug or find the test case where my code is failing .
I am getting WA on test case 3
Someone please help
why this solution for C is giving TLE link
It's a great solution and tutorial!! Thank you very much!!
E2 editorial is impossible to understand even if you've already solved the problem before. (or it's just me being weak)
UPD: nah, it's ok.
getting wrong ans in tc3 at last tc..can anyone explain whats wrong in this method bcoz that tc is at very end so its hidden!
There is a simpler DP solution for E1 that does not require binomial coefficients.
Let $$$f_{i, j}$$$ be the number of different deterministic max-heaps and $$$g_{i, j}$$$ be the number of different trees, both with size $$$2^i - 1$$$ and produced by applying $$$j$$$ operations.
By using prefix sums for optimization, the total time complexity is $$$O(nk^2)$$$ with a small constant factor. Code