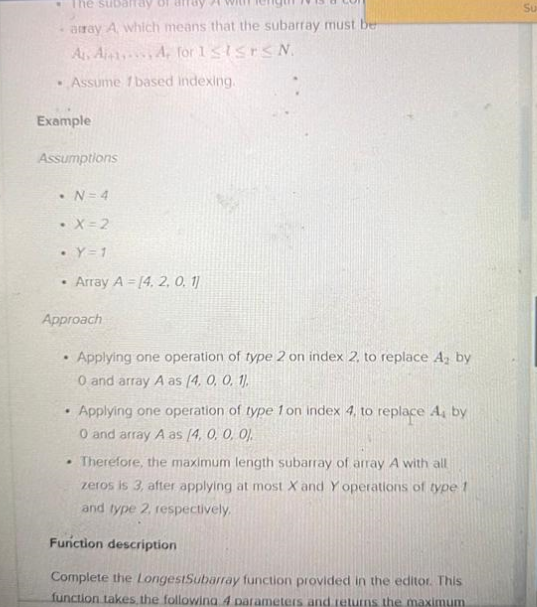
Two type of operations
Type1: replace A[i] by A[i]-1
Type2: Replace A[i] to 0.
Determine maximum length of subarray that can be obtained if all elements of subarray are zero and you can apply max operations of x and y of type 1 and 2 respectively.
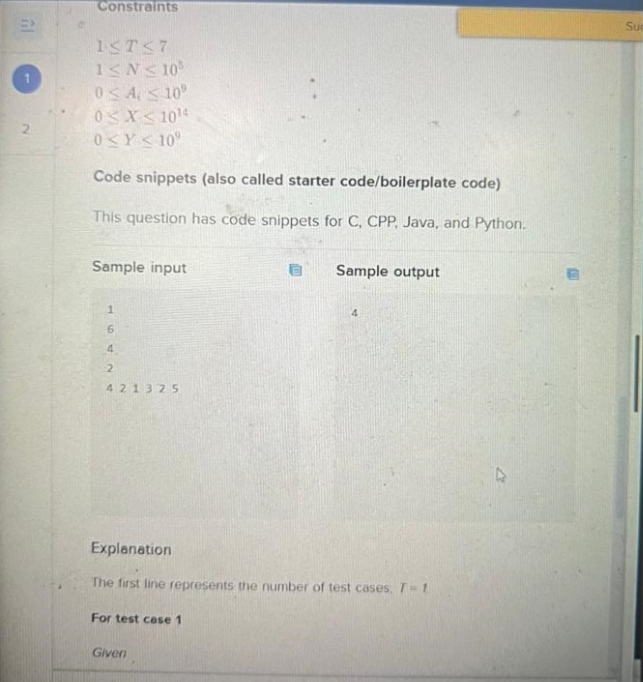
Constraints: 1<=T<=7
1<=N<=1e5
0<=A[i]<=1e9
0<=Y<=1e9
0<=X<=1e14.
Reference Images: 











we can binary search on answer length of subarray
Like yeah i got his idea but i am not getting a 0(n) solution even to check if that length mid satisfies, like in detail say me how to check that??
let's say you are checking if you can find a subarray with length of at least $$$mid$$$
iterate through all subarrays of size $$$mid$$$ and keep a $$$cnt$$$ of how many $$$0$$$ elements in each subarray
if there's a subarray with $$$mid-cnt <= x+y$$$, then you can turn that whole subarray into $$$zeros$$$
there's an edge case when $$$x=0$$$, then you can only use the subarrays that starts with a $$$0$$$
this should be $$$O(n)$$$
Like i am sorry, the initial post was wrong, like see now i have corrected the question can you explain it to me now
now i'm not sure if i understand correctly...
why does the sample test gives $$$4$$$? the way i understand it should be $$$6$$$
I have changed the question its A[i]=A[i-1], its changed to A[i]=A[i]-1.
so for every subarray of size mid, smallest elements should be used first to exhaust all ops of type 1, then after that remaining elements<=y.
Sorry for the late reply :(
Lets do a different approach. For each index $$$l$$$, let it be a potential start of our subarray and find $$$f(l)$$$ as the furthest end away from l that we can turn the subarray $$$[l,f(l)]$$$ into zeros
If $$$a[l]==0$$$ and we found a potential end $$$r$$$, we pick $$$x$$$ largest elements in $$$[l,r]$$$ and apply opertaion $$$1$$$ to turn them to zeros, and the other elements we can chip away with operation $$$2$$$. So to be able to turn $$$[l,r]$$$ into zeros, we need to satisfy $$$Sum(l,r)-SumOfBig(l,r)<=y$$$, with $$$SumOfBig$$$ meaning the sum of the X biggest elements in $$$[l,r]$$$
If $$$a[l]!=0$$$,we use up one of the first type operation to make it $$$0$$$, and find $$$f(l)$$$ similarly like case above
$$$Sum(l,r)$$$ can be done in $$$O(1)$$$ with prefix sum; and we can find $$$SumOfBig(l,r)$$$ in $$$O(log(n)^2)$$$ with binary search, combined with Persistent Segment Tree or Persistent Fenwick Tree.
Our complexity for each potential $$$r$$$ is $$$O(log(n)^2)$$$ so we cant afford another binary search. Use 2 pointers instead.
However there's an easy mistake to fall into. Unlike normal 2 pointers, here $$$f(l)$$$ can be less than $$$f(l+1)$$$ because we must waste a first type operation if the second case occurs for $$$l+1$$$. So we need to do 2 pointers seperately for the 2 cases. I guess my explanation for doing the 2 pointers seperately might be unclear, if you are not sure about it you can ask later :D
Edit: just finished dinner :) my solution above is $$$O(n*log^2)$$$ but we can inprove it to $$$O(n*log)$$$
instead of using persistent data structures combined with binary search, as you move the pointers you can insert elements into a BST(for example Treap) or a skiplist
Is this an ongoing online assessment?
No completed yesterday night.
Auto comment: topic has been updated by conan45 (previous revision, new revision, compare).
Auto comment: topic has been updated by conan45 (previous revision, new revision, compare).
You can work this with 2 pointers maintaining the start and end points of a subarray while also keeping Y largest elements that are present in that subarray which are done by type-2 operation and making sure that all the elements that are not a part of Y largest elements are done by type-1 operation.
Auto comment: topic has been updated by conan45 (previous revision, new revision, compare).
yes