Problem D2: Line of Delivery (Part 2) Link
Hello everyone, I'd like to talk about Problem D2 from the recent Meta Hacker Cup 2024 Practice Round. The solution suggests that we can use a treap data structure to efficiently handle the operations described in the problem.
Operation 1) Insert a stone at $$$E_i^{th}$$$ empty position.
Operation 2) Move all stones to the left of the inserted stone by 1 unit in the negative direction.
Yes, treaps can be used to solve this problem, but I’ve come up with a simpler solution using a vector approach. Let's maintain an array called emptyPlaces that stores information about all the empty spots. In this array, I track how many balls are located immediately to the right of each empty position. So emptyPlaces[i] denoted how many consecutive balls are immediately right towards $$$i^{th}$$$ empty slot. Additionally, I keep a start pointer to mark the current starting position in the array.
So the above 2 operations can be modified as follows:
Operation 1) emptyPlaces[start + Ei - 1]++; (0-based indexing)
Operation 2) start++; Just moving the start pointer can handle the shifting case mentioned in operation 2) above.
The key advantage of this approach is that we shift the stones to the left of the newly inserted stone by 1 unit in the negative direction. This can be visualized as adding an empty spot to the left of the inserted stone and removing the first empty position from the array.
Example:

Here in this case, the emptyPlaces array looks like $$$[0,1,2,1,0,0]$$$
Let's say a ball is thrown with $$$E = 4$$$, then the $$$4^{th}$$$ empty position is occupied by this new red ball.
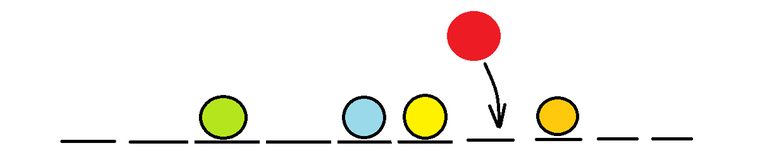
Now Since this new ball has collided with the previous 3 balls at position 3,5,6 then these balls move 1 unit towards left.
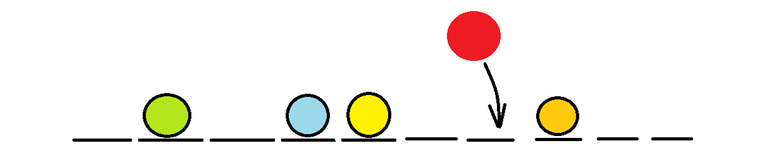
This can be visualized like adding a new empty slot on left of new ball, and deleting an empty slot at the start of the track.
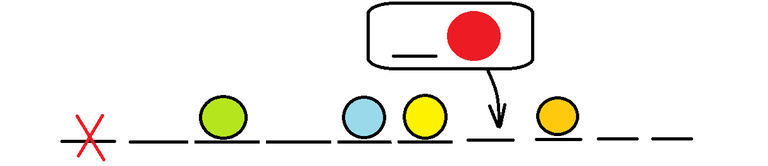
Now if we notice the emptyPlaces array, it changes to $$$[1,2,2,0,0]$$$. After adding the empty slot and new ball combined to $$$4^{th}$$$ position, the emptyPlaces array changes to $$$[0,1,2,2,0,0]$$$. Since the previuos balls move 1 unit left, we can delete the first element in emptyPlaces array and it changes to $$$[1,2,2,0,0]$$$.
Just maintaining these could get me all the distinct positions of the final balls, and since the thrown balls are in order toward the negative x direction, finding the position of each ball is relatively easy.










Auto comment: topic has been updated by ASHWANTH_K (previous revision, new revision, compare).
A simple O(n^2) solution also runs fast enough on modern CPUs. My code ran for ~50 seconds for the whole input, and for the sake of experiment I also parallelized the testcases, which decreased the runtime to ~10 seconds. If a faster input is done (buffering instead of std::cin) then it probably will run a bit faster as well!