Thanks to t.ravnushkin for helping in writing contents of this blog. Thanks to Alexdat2000 for proof-reading and to bashkort for announcing the month of blog posts. Even though I have started writing this blog before the announcement it would have probably been left in a trash bin due to my laziness.
Introduction
Matching is a beloved topic throughout competitive programming community due to its simple nature and fun applications. Matchings are not only useful in graph theory, but are also essential in topics such as game theory, partially ordered sets and combinatorics. In this blog we are gonna talk about less known applications of the subject. The main goal of the blog is explaining the intuition behind being able to associate the number of some combinatorial species to the amount of perfect matchings and understanding when it is possible to efficiently compute their counts. The blog mainly consists of two parts: one covering more general approach and the other one covering more combinatorial technique called graphical condensation which is applicable to some of the matching problems.
Prerequisites: basic linear algebra knowledge, gaussian elimination algorithm. Basically being able to compute determinant in $$$O(n^3)$$$ or having trust in possibility of doing so is enough .
Determinant and permanent of a matrix
This section can be a bit trivial if you already have some linear algebra knowledge, so feel free to skim through it.
As a reminder determinant is the following expression associated with a matrix $$$A$$$:
Here $$$S_n$$$ is the symmetric group of size $$$n$$$. You can consider $$$S_n$$$ to be a set of all permutations of size $$$n$$$. So our expression boils down to summation over all permutations. Next we define sign of a permutation $$$\text{sign}(\sigma) :=(-1)^{\text{N}(\sigma)}$$$ where $$$\text{N}(\sigma)$$$ is number of inversions in $$$\sigma$$$.
Determinant is an object of a high interest in mathematics due to its many properties. It works as an oriented multidimensional volume of parallelotopes in $$$n$$$ dimensional spaces. It is essential in classification of operators when used in characteristic polynomials. However in the blog we are only going to use the fact that determinant can be computed in $$$O(n^3)$$$ time. Fast computational time (I mean polynomial at least ugh ...) and sophisticated form is going to allow us to compute difficult things in a reasonable time.
Another expression we are going to encounter today is permanent of a matrix $$$A$$$:
Notice that the expression looks very similar to the one of determinant however we do not multiply by permutation sign. Simpler look of the formula comes with a great cost. Valiant's theorem states that even with values of $$$A$$$ being restricted to $$${0, 1}$$$ the permanent is a $$$\verb|#|P$$$-complete problem. We will actively try to overcome this obstacle.
Motivation
Let's apply these newly learned definitions to do something cool. For now we will try to learn how to find if a perfect matching exists in some bipartite graph. Obviously we will only consider graphs where sizes of both parts are equal. For now let's build adjacency matrix $$$A$$$ of the graph. Next we will use the following idea: each summant in determinant corresponds to some perfect matching in our graph.
When we will talk about some edge $$$(u,v)$$$ $$$u$$$ will denote vertex from the first part and $$$v$$$ will denote vertex from the second part. Consider the following graph on $$$8$$$ vertices:
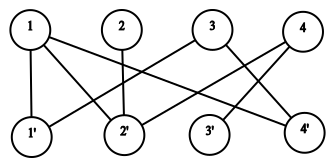
Corresponding adjacency matrix looks like this:
Then, let's consider permutation $$$\sigma = \left(4, 2, 1, 3\right)$$$. Notice that we can associate a perfect matching with it $$$(1, 4'), (2, 2'), (3, 1'), (4,3')$$$. Now we can get an idea of finding determinant of the following matrix. If it is non-zero it guarantees us that at least one summant of sum over all permutations is not zero so perfect matching exists. However it might appear that determinant becomes zero even if perfect matching exists. Counter example is very simple since we can take any full bipartite graph.
That allows us to come up with simple random algorithm for checking existence of perfect matching. We put $$$A_{i,j} = 0$$$ for non-existent edges and $$$A_{i, j} = c_{i, j}$$$ for existent edges where $$$c_{i, j}$$$ is some random value independent for each cell. We will not provide further details since further we will only need the concept of this idea but for more detailed explanation you can check out Randomized general matching with Tutte matrix
Permanent and the number of perfect matchings
Now let's take a look at the permanent again:
Notice that if $$$A$$$ is adjacency matrix of a bipartite graph then permanent counts exactly number of perfect matchings. Every perfect matching will correspond to some permutation and it will be counted in the sum only if all edges in it exist in our graph. As we have mentioned counting permanents is hard but counting determinants is easy so now we will introduce some assumptions under which we can reduce counting permanents to counting determinants. What if we somehow find a way to make entries of $$$A_i$$$ equal to $$$\pm 1$$$ in such a way that signs of permutations cancel out? Such signing is called Kasteleyn signing.
For the sake of simplicity everywhere below we will assume that graph contains no duplicate edges. First, we will show one sufficient condition for signing to be Kasteleyn:
Definition 1. Cycle $$$C$$$ in graph $$$G$$$ is called evenly-placed if there exists a perfect matching on vertices $$$G \setminus C$$$.
Notice that since perfect matching can only exist on graphs with even number of vertices we can consider $$$C$$$ to be even-lengthed in our endeavors.
Definition 2. Let $$$C$$$ be an evenly-placed cycle of length $$$2l$$$. If the number of edges with negative weight on $$$C$$$ is of the opposite parity to $$$l$$$, $$$C$$$ is called properly-signed.
Lemma 1. For a signing to be Kasteleyn it is sufficient that every evenly-placed cycle is properly-signed.
For the proof let's consider some perfect matching $$$M$$$ with corresponding permutation $$$\sigma$$$. We define sign of a matching so we need to show that
is the same for any perfect matching. In other words, we have to show that $$$\text{sign}(M)\text{sign}(M')=1$$$ for any pair of perfect matchings $$$M$$$ and $$$M'$$$. Let's rewrite the last equality as
That form gives us an idea to consider the symmetric difference (the set of all elements which are in either of the sets, but not in both simultaneously). It's a common trick used to prove matching identities and can help us here too.
Let's rewrite our equality to obtain
Let's show that $$$\displaystyle \text{sign}(\sigma) = \text{sign}(\sigma') \prod_{e \in M \triangle M'} A_{e_1, e_2}$$$ from which we get $$$\text{sign}(M)\text{sign}(M') = 1$$$ (because all integers here are either -1 or 1) and that would end the proof.

The first matching M consists of green and yellow edges, the second one — of red and yellow. Therefore, their symmetric difference consists of red and green edges.
To show the required identity let's consider $$$e \in M \triangle M'$$$. Since $$$M$$$ and $$$M'$$$ are perfect matchings, their symmetric difference only consists of even-length cycles. All these cycles are of length at least $$$4$$$ since they lie in symmetric difference. One can easily notice that any such cycle is evenly placed (ugu aga easily seen with picture). Let the length of $$$i$$$-th such cycle be $$$2l_i$$$ and the total number of those $$$c$$$.\ Let's take an arbitrary cycle $$$C$$$ of those in symmetric difference. Because $$$C$$$ is evenly-placed, $$$C$$$ is also properly-signed, which means
From which immediately follows
But notice that to make $$$\sigma$$$ from $$$\sigma'$$$ it is enough to make $$$\displaystyle \sum_{i=1}^{c} (l_i - 1)$$$ transpositions. That is so because for each cycle we can do $$$l_i - 1$$$ transpositions to fix $$$l_i-1$$$ positions and the last one will get fixed automatically. So $$$\displaystyle \text{sign}(\sigma) = \text{sign}(\sigma')\prod_{i=1}^{c}(-1)^{l_i - 1}$$$ and that concludes the proof.
Theorem 1. There exists a Kasteleyn signing for any graph $$$G$$$ satisfying all of the following properties:
$$$G$$$ is bipartite.
$$$G$$$ is planar.
$$$G$$$ is 2-connected.
For the proof of the theorem let's use the following lemma
Lemma 2. If the boundary cycle of every inner face of bipartite, planar, 2-connected graph $$$G$$$ is properly-signed then signing is Kasteleyn.
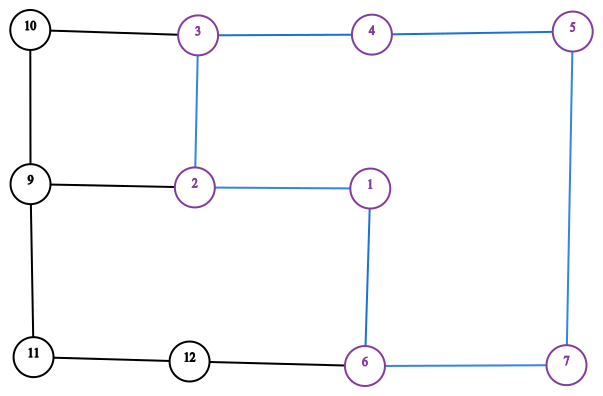
The figure shows a planar graph with the boundary cycle of one inner face of $$$G$$$.
To prove that signing is Kasteleyn, we only need to show that any evenly-placed cycle $$$C$$$ of length $$$2l$$$ is properly-signed. We will show that properly-signedness of all cycles corresponding to inner planes implies proper-signedness of any evenly-placed cycle $$$C$$$. To do so, we are going to use Euler's formula. First, let's fix some planar drawing of our graph. Then Euler's formula states that with number of faces $$$F$$$, number of vertices $$$V$$$ and number of edges $$$E$$$ holds $$$V - E + F = 2$$$. Select a cycle $$$C$$$ and take a graph located fully inside it in our planar drawing. Let $$$k$$$ be number of inner planes enclosed by our cycle $$$C$$$. Let's apply Euler's formula to our case:
$$$V = 2l + I$$$, where $$$I$$$ is the number of interior points of our graph.
$$$E = l + l_1 + \ldots + l_k$$$, where $$$l_i$$$ are the halved lengths of inner cycles. This is the place where we use 2-connectivity. Each edge is incident to exactly $$$2$$$ planes (including outer one).
$$$F = k + 1$$$ (including outer plane).
Then by Euler's formula we get:
Using that $$$C$$$ is evenly-placed we know that $$$I$$$ is even (or otherwise there would be no perfect matching). Applying this fact and doing a little rewriting we obtain:
Now just bear this formula in mind as we will use it in a moment. For now, notice that every edge is used on exactly two cycles of $$$C$$$, $$$C_1$$$, ..., $$$C_k$$$ (we consider all inner cycles which are enclosed by our composite cycle $$$C$$$) so the total number of $$$-1$$$ values on cycles is even. Let's denote $$$n_C$$$ as number of values on the cycle $$$C$$$ then:
or equivalently
By applying properly-signedness of $$$C_1, \ldots, C_n$$$ we get
In the last equivalence we applied a formula which we discovered before so we obtain that $$$C$$$ is properly-signed and this finishes the proof.
Now it becomes trivial to formulate the algorithm. First, choose any spanning tree of $$$G$$$. Second, add edges in such order that no more than $$$1$$$ new inner plane appears. After the addition of a new edge we only need to worry about signing of the cycle enclosed by this new inner plane (that statement is due to Lemma 2).
That concludes the long and elaborate part about the general idea of what we are doing here.
Some discussion and extensions.
First question that should be asked is whenever conditions could be simplified. We will start with removing 2-connectivity. I would recommend trying to coming up with solution yourself but here I provide short explanation if needed.
Next we will briefly discuss planarity. There are some extensions which allow us to count matchings in non-planar graphs. It is known that any graph which does not have $$$K_5$$$ or $$$K_{3,3}$$$ is planar. $$$K_5$$$ here means clique of $$$5$$$ vertices and $$$K_{3, 3}$$$ means complete bipartite graph with left and right parts having $$$3$$$ vertices. Most of the extensions to non-planar graphs focus on counting perfect matchings under slightly lighter conditions for example in $$$K_5$$$-free graphs (Straub et al. 2014) or counting perfect matchings in $$$K_{3,3}$$$-free graphs (Little 1974, Vazirani 1989). Those algorithms mostly rely on careful analysis of higher order connectivity properties (i.e. $$$3$$$-connectivity, $$$4$$$-connectivity etc). However planar graphs family has the least convoluted results with much more pleasant ideas behind them.
The last condition we could try to relax is bipartiteness. There exists more general version of the theorem called Kasteleyn's theorem. It allows us to count number of perfect matchings in any planar graph. May be we will write part 2 of this blog in the future but since we start to worry about length of this one we will leave this part for the curious people to read about by themselves.
Graphical condensation
In this section we will try to find some interesting relations between domino tilings of some grids with their subgrids.\ First, let's consider a usual rectangular grid (let's call it $$$F$$$). Now, let's mark its corners a, b, c and d in clockwise order, and let $$$F_{i_1,i_2,...}$$$ denote $$$F$$$ with corners $$$i_1, i_2, ...$$$ removed. Also, let's write "the number of domino tilings of $$$F$$$" as $$$\verb|#|F$$$.
Theorem 2. $$$\verb|#|F\verb|#|F_{abcd} = \verb|#|F_{ab}\verb|#|F_{cd}+\verb|#|F_{ad}\verb|#|F_{bc}$$$
As a proof we will show how one can construct a pair of tilings of either $$$F_{ab},F_{cd}$$$ or $$$F_{ad},F_{bc}$$$ from a pair of tilings of $$$F,F_{abcd}$$$, therefore showing these sets have the same number of elements.
First, consider a superimposition of a tiling of $$$F$$$ and a tiling of $$$F_{abcd}$$$. Notice that it is a graph that consists either of cycles that do not contain corners of our grid, or paths that begin in one corner and end in another. One can easily see that a path beginning in $$$a$$$ can't end in $$$c$$$, since otherwise $$$b$$$ and $$$d$$$ can't be connected with any other corners.
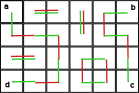
The tiling of $$$F$$$ consists of green edges whereas the tiling of $$$F_{abcd}$$$ of red ones.
Second, let's construct another pair of tilings from this superimposition — take all the edges $$$F$$$ into the first one and ones from $$$F_{abcd}$$$ into the second one, but invert the colors of the edges located on the path from $$$b$$$ to $$$c$$$ (situation of path from $$$b$$$ ending in $$$a$$$ is analogous).
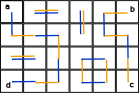
Notice that the tiling consisting of orange edges is a tiling of $$$F_{ad}$$$ and of the blue ones is of $$$F_{bc}.$$$
With this we have showed the required construction, which concludes the proof.
This theorem can be generalized to any bipartite graph with the only requirement being that $$$a,c$$$ are in the same part and $$$b,d$$$ belong to the other one. The proof of this fact uses the same technique so we will skip it to keep our blog a little shorter.
Now, let's consider a bit more interesting of a scenario.
Definition 3. An aztec diamond of order $$$n$$$ is a figure on a grid that consists of all unit squares whose centers satisfy $$$|x| + |y| \leq n$$$.
Let $$$AD(n)$$$ denote the number of domino tilings of an aztec diamond of order $$$n$$$. We'd like to prove $$$AD(n)AD(n-2) = 2AD(n - 1)^2$$$.
Take the squares located at $$$(-n+1.5,-0.5),(-0.5,n-1.5),(n-1.5,0.5),(0.5,-n+1.5)$$$ as $$$a,b,c,d$$$. One can easily notice that with such squares selected our task satisfies the constraints or the generalised version of Theorem 2.

An aztec diamond of order 4 with selected cells marked.
Now, let's find out what the tilings of our diamond with removed squares look like:
The removal of all four selected cells fixes the tiling of the entire border of our diamond, therefore is equivalent to a tiling of a diamond of order $$$n - 2$$$ (the number of these is $$$AD(n-2)$$$.
The removal of two consecutive squares (out of selected ones, of course) fixes the tiling of half the border, and the number of these is therefore $$$AD(n-1)$$$.
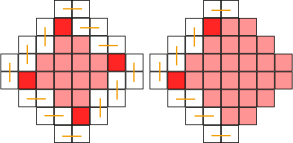
The first and second situations portrayed (red cells are the removed ones while the remaining diamond is comprised of pink ones).
Therefore, we have proven
To solve the reccurence, we can notice that taking a logarithm of both sides we obtain
Now you obtain a simple linear recurrence by solving which we obtain $$$AD(n) = 2^{n(n+1)/2}$$$ and are finished.
We end this section with a pretty funny application of the technique. It happens that the amount of plane partitions can be related to the amount of perfect matchings. For the proof using systems of paths you can check the following blog by miaowtin. To relate the amount of partitions to the number of matchings consider a hexagon with opposite sides equal to $$$r,s,t$$$. One can easily see that such a hexagon can be partitioned into a grid of right triangles. Now, consider its tilings into rhombuses comprised of two such triangles. As we already know, it corresponds to some perfect matching. One can see that this is an orthographic projection of some 3D Young tableau, and this is actually a bijective relation between the two. On the picture green tiles correspond to the top parts of cubes of the plane partition, orange ones — to the sides of cubes oriented to one side and the purple tiles — to the sides of cubes oriented to the other side.
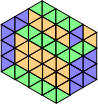 $$$~~~~~~~~~$$$
$$$~~~~~~~~~$$$ 
Notice that the angles of rhombuses define side orientation.
Since hexagonal grid is bipartite, we could count the number of partitions using the method with Kasteleyn's signings, but there exists a neat formula.
The number of such tilings (Young tableaux) is (MacMahon formula)
A very hard exercise. Prove MacMahon formula using graphical condensation for this grid of triangles. Proof using condensation is not very complex but technical and would need us to use generating functions, q-binomials and other fun stuff which is not fun to define again. Since this blog is already long enough, we might cover this in some future blog, but for now we leave you only with this cool-looking projection idea.
Applications
This blog would be total garbage if it did not have good applications. As an example of problems solveable with described techniques we list problem 1339A. After reading this blog you will hopefully know that the problem asks you to count number of plane partitions in a box $$$1 \times 1 \times n - 1$$$. To count number of such partitions you could use Kasteleyn's signings and solve it in $$$O(n^3)$$$ or use MacMahon's formula or notice that number of ways to stack cubes in a tube of height $$$n - 1$$$ is $$$n$$$. Shocking! Now you know proper way to solve the task without any ad-hoc thinking skills!











I usually don't like technical math with proofs, but this blog was honestly interesting!
As a co-author, please share contribution!
Finally, a good pancakes recipe!
deer crackers
Speaking of which, let me share something I worked on last year—a theoretical algorithm that counts perfect matchings in $$$2^{n-\Omega(\sqrt n)}$$$ time! (Unfortunately, the hidden constant behind $$$\Omega$$$ is too small to have practical implications...) Interestingly, I posted the preprint on arXiv exactly one year ago today.
I am a bit confused. Are you not aware of algorithms counting matchings in $$$O(1.618^n)$$$ and $$$O(2^{\frac{n}{2}})$$$? They seem faster than what you claim and are contests-implementable
EDIT: Ah, ok, I get it. You meant bipartite graphs that have n vertices on each side, so 2n vertices in total, while in the algorithms that I meant, n was the total number of vertices (for not necessarily bipartite graphs). I guess that makes sense as the blog is about bipartite graphs :p