Hi Codeforces!
This is my first attempt at a tutorial blog XD.
Disclaimer: No headaches occured during the making of this blog
Problem statement
Given an integer array $$$A$$$ of length $$$n$$$ and $$$q$$$ of the following 5 types of queries:
- For all $$$i \in [l,r]$$$, change $$$A_i$$$ to $$$\max(A_i, v)$$$
- For all $$$i \in [l,r]$$$, change $$$A_i$$$ to $$$\min(A_i, v)$$$
- For all $$$i \in [l,r]$$$, change $$$A_i$$$ to $$$A_i + v$$$
- For all $$$i \in [l,r]$$$, change $$$A_i$$$ to $$$v$$$
- Output $$$A_i$$$
- $$$ 1 \leq n,q \leq 10^6 $$$
- $$$ 1 \leq l \leq r \leq n $$$
- $$$ -10^9 \leq A_i, v \leq 10^9 $$$
The above is solvable with techniques like Segment Tree Beats in $$$\mathcal{O}(n+q\log^2{n})$$$, but as a binary search enthusiast, you didn't learn segment tree beats?
Don't worry, here's an easier, faster, and shorter solution that solves this particular problem in $$$\mathcal{O}(n+q\log{n})$$$
Prerequisites
You should know the following to solve the full problem:
- Basics of functions (including composite functions)
- Associative, commutative, and distributive properties of $$$\max$$$ / $$$\min$$$
- Basics of a lazy propagation segment tree (not required for some subproblems)
Assuming you know the above, let's begin! But first, I'll relax the constraints a bit...
Subproblem 1
These are the queries:
- For all $$$i \in \textbf{[1,n]}$$$, change $$$A_i$$$ to $$$\max(A_i, v)$$$
- For all $$$i \in \textbf{[1,n]}$$$, change $$$A_i$$$ to $$$\min(A_i, v)$$$
Print the final array $$$A$$$ $$$\newline$$$
We'll use the example input to try coming up with a solution to this problem.
Let $$$f_i(x)$$$ = output after applying only $$$i$$$th query to integer $$$x$$$
Let's define a composite function $$$F(x)$$$ = $$$f_Q(f_{Q-1}(\dots f_2(f_1(x))\dots))$$$
We basically want to output $$$F(x)$$$ for all $$$x \in A$$$
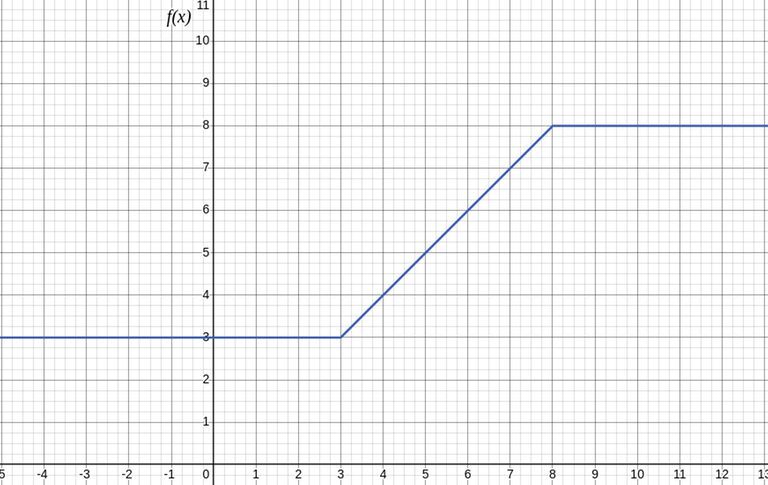
We can try plotting the graph of $$$F(x)$$$ against $$$x$$$ to hopefully find a pattern.
Some observations about the above graph.
- $$$F(x)$$$ is monotonically non-decreasing i.e. $$$F(x) \leq F(x+1)$$$
- The graph can be divided into 3 sections depending on $$$x$$$:
In other words, $$$F(x) = \min(8,\max(x,3))$$$
In fact, it can be proven that $$$F(x) = \min(a,\max(x,b))$$$ for constants $$$a$$$, $$$b$$$ in the general case.
From the mathy proof, we can repeatedly spam $$$f_{i+1}(f_i(x))$$$ till we get $$$F(x)$$$.
Our starting $$$ f_0(x) = \min( \infty , \max( x, -\infty ) ) $$$ as this does not affect $$$x$$$
Now, that we have calculated our $$$F(x)$$$ in $$$\mathcal{O}(Q)$$$ , we can use it to calculate our final array in $$$\mathcal{O}(1)$$$ per $$$x$$$.
From the intuitive proof, we can create this solution:
Bonus: Solve this subproblem using $$$\max(a,\min(x,b))$$$ instead.
Ok, that was easy enough. Let's make it a bit harder.
Subproblem 2
These are the queries:
- For all $$$i \in [l,r]$$$, change $$$A_i$$$ to $$$\max(A_i, v)$$$
- For all $$$i \in [l,r]$$$, change $$$A_i$$$ to $$$\min(A_i, v)$$$
- Output $$$A_i$$$ $$$\newline$$$
In the first subproblem (mathy solution), we applied $$$f_i(x)$$$ to the entire array for each $$$i \in [1,q]$$$, but now we want to apply $$$f_i(x)$$$ only to $$$l_i, r_i$$$ for each $$$i \in [1,q]$$$. Doing this naively will take $$$\mathcal{O}(nq)$$$ time which is too slow.
We can speed this up with lazy segment trees instead. The idea is to only apply $$$f_i(x)$$$ to the $$$\mathcal{O}(\log n)$$$ segment tree nodes and lazily push down these functions from a segtree node to its children only when necessary (to make sure we apply the functions in the correct order).
Each node in the segment tree will contain the pair of integers $$$[a,b]$$$ which determines the function that is currently applied to that node (and eventually, all its decendants). Initially, each node's $$$[a,b]$$$ represents $$$f_0(x)$$$ and hence is equal to $$$[\infty,-\infty]$$$.
We apply to the $$$\mathcal{O}(\log n)$$$ nodes in the range $$$l_i, r_i$$$ for each query. Along the route to the target nodes, we push down the current node's $$$[a,b]$$$ to both children(if it's not $$$f_0(x)$$$) (to preserve order). $$$\newline$$$
Bonus: Solve this subproblem using the intuitive solution instead.
Ok, now we're getting somewhere. It's still not hard enough though...
Subproblem 3
These are the queries:
- For all $$$i \in \textbf{[1,n]}$$$, change $$$A_i$$$ to $$$\max(A_i, v)$$$
- For all $$$i \in \textbf{[1,n]}$$$, change $$$A_i$$$ to $$$\min(A_i, v)$$$
- For all $$$i \in \textbf{[1,n]}$$$, change $$$A_i$$$ to $$$A_i + v$$$
Print the final array $$$A$$$ $$$\newline$$$
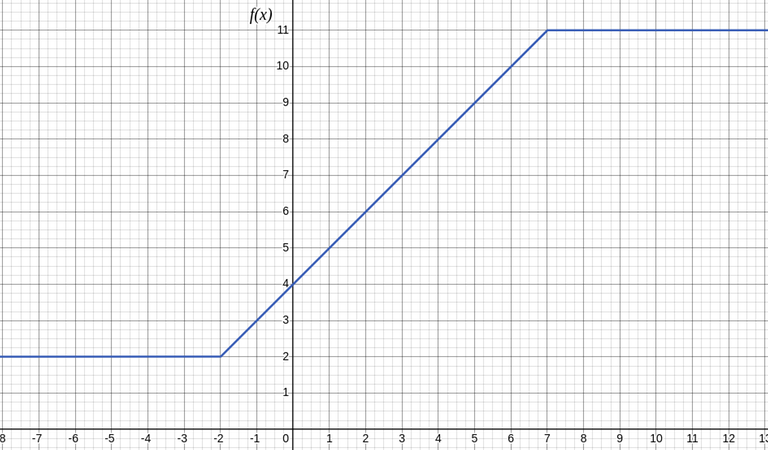
The example input3 is exactly the same as the example input1, but I added a couple of type 3 queries. We'll use example input3 to observe a pattern. On to plotting...
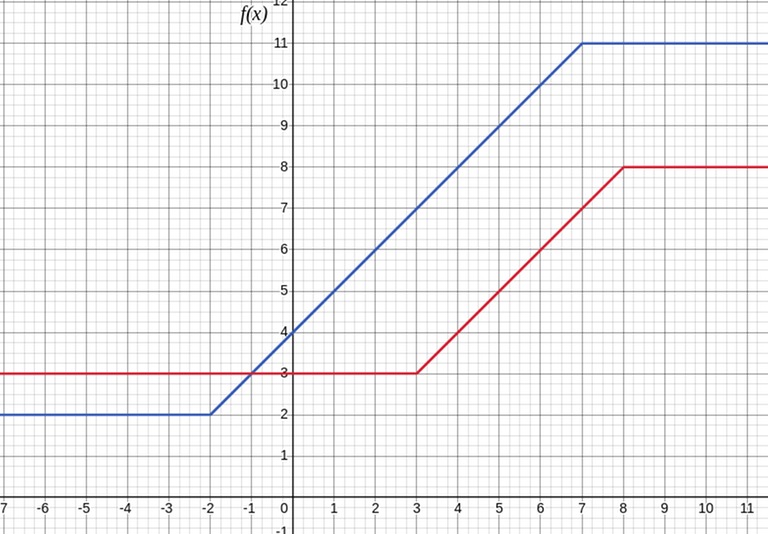
It seems both graphs have the same structure. Let's compare both of them.
The new graph has the same 3-part structure as the old one, but with a horizontal translation by some $$$c$$$ for some new constants $$$a,b,c$$$
In other words:
$$$\displaystyle F(x) = \min(a,\max(b,x+c))$$$ for constants $$$a, b, c$$$ in the general case.
Proof is quite similar to the first subproblem.
Our starting $$$ f_0(x) = \min( \infty , \max(-\infty, x+0) ) $$$ as this does not affect $$$x$$$
From the intuitive proof, we can create this solution:
Bonus: We could also interpret the new graph as a vertical translation. Solve this subproblem using $$$\max(a,\min(x,b))+c$$$ instead.
Original problem
Armed with the ability to solve subproblems 1, 2, and 3, you should now be able to solve the original problem. Try solving it first : D
How to solve? It's just subproblem 2+3 with an extra step
Bonus: Solve this problem using the intuitive solution instead.
Final time complexity: $$$\mathcal{O}(n+q\log{n})$$$
Practice problems
I'll update this list if you find any more problems
Conclusion
Thanks to madlogic for proofreading this blog and useful suggestions!
If you found this trick useful, you might as well upvote :)
In the case of any bugs or questions, feel free to let me know.











DAN4LIFE ORZ!!!!
MR.WHITEBIRD ORZ!!!!
Can you show the details for "Handle range queries?". As far as I can see it won't work and saying that this can replace seg tree beats for this type of problem is a sort of a big claim imo.
Didn't say it works for range queries, just pointed out that segtree beats can solve harder variations and is overkill in this case
Yes, lazy propagation can do many types of range-range operations — as long as you can combine updates into $$$O(1)$$$ info in a node.
But please remove the segment tree beats from the title. You're wasting time of people who think that you're proposing its easier replacement. It doesn't help that the following sentence doesn't clearly say if you can do the sum:
Sure. I've made the blog less confusing.
The idea is not related to chmin, cmax, add, and assign per se. It's just a general idea: if there is some constant $$$k$$$ such that any sequence of $$$k+1$$$ updates to a sequence of numbers can be shrunk to a sequence of $$$k$$$ updates, we can use lazy segment trees to store these updates. Then, if we only care about point queries, we can already answer them. However, if we want to answer queries of calculating some function $$$F$$$ on a segment, we also need to be able to quickly (ideally, in constant time) recalculate the value of $$$F$$$ on a segment after the application of a single update to all the elements of this segment. Hence, for example, if our query is "sum all the elements on a segment", segment trees are good to go with updates like add and assign and fail with updates like chmin and chmax. On the other hands, if our query is "find minimum on a segment", there is no trouble to add chmin and chmax updates.