Here is the Link of the topcoder problem Link i read its editorial but not able to get it would anyone like to help me to understand this ??
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3985 |
| 2 | jiangly | 3814 |
| 3 | jqdai0815 | 3682 |
| 4 | Benq | 3529 |
| 5 | orzdevinwang | 3526 |
| 6 | ksun48 | 3517 |
| 7 | Radewoosh | 3410 |
| 8 | hos.lyric | 3399 |
| 9 | ecnerwala | 3392 |
| 9 | Um_nik | 3392 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 169 |
| 2 | maomao90 | 162 |
| 2 | Um_nik | 162 |
| 4 | atcoder_official | 161 |
| 5 | djm03178 | 158 |
| 6 | -is-this-fft- | 157 |
| 7 | adamant | 155 |
| 8 | awoo | 154 |
| 8 | Dominater069 | 154 |
| 10 | luogu_official | 150 |
→ Find user
→ Recent actions
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Dec/22/2024 12:59:56 (k1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|










Take it like this:
There must be a 1-coin. Suppose you took k 1-coins, then you can't make k + 1 in any way other than by one k + 1-coin. Now, you have ways to make all values up to 2k + 1. Suppose you took l k + 1-coins. Then you can make all values up to l(k + 1) + k, each exactly once. Again, you need a coin with cost l(k + 1) + k + 1 = (l + 1)(k + 1) to achieve the next value. That looks suspicious: in fact, if you have xi coins of the i-th type, the next coin must have value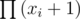 .
.
That means if we sorted the coin types that we take at least 1 coin into a sequence of xi, then xi - 1 divides xi and there must be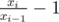 coins of type i - 1; the number of coins of the last type can be chosen easily based on the fact that if it's k, then we can make all values up to kxn - 1.
coins of type i - 1; the number of coins of the last type can be chosen easily based on the fact that if it's k, then we can make all values up to kxn - 1.
And now that we know how many coins to use, we can do a DP on the total number of coins used for types starting with the i-th, in O(N2). I leave that up to you.
thanx Xellos
TopCoder SRM 195 Div 2, Level Three, ChangePurse, Advanced Math. (written for bare purpose of web crawlers to index the page and associate it with related query. wish it was done by tags and headers)