I'm having some difficulties with this problems? Can you help me?
I think it can be solved by using Dynamic programming on tree, isn't it?
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3985 |
| 2 | jiangly | 3814 |
| 3 | jqdai0815 | 3682 |
| 4 | Benq | 3529 |
| 5 | orzdevinwang | 3526 |
| 6 | ksun48 | 3517 |
| 7 | Radewoosh | 3410 |
| 8 | hos.lyric | 3399 |
| 9 | ecnerwala | 3392 |
| 9 | Um_nik | 3392 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 169 |
| 2 | maomao90 | 162 |
| 2 | Um_nik | 162 |
| 4 | atcoder_official | 161 |
| 5 | djm03178 | 158 |
| 6 | -is-this-fft- | 157 |
| 7 | adamant | 155 |
| 8 | Dominater069 | 154 |
| 8 | awoo | 154 |
| 10 | luogu_official | 150 |
I'm having some difficulties with this problems? Can you help me?
I think it can be solved by using Dynamic programming on tree, isn't it?
| Name |
|---|



I will describe solution, which complexity seems to be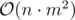 , but it passed in 0.31 sec (I don't know how, maybe tests are very weak, maybe it will pass any test).
, but it passed in 0.31 sec (I don't know how, maybe tests are very weak, maybe it will pass any test).
First, we have rooted tree, where root is vertex 1. Every vertex (except root) has a parent. We need to find subtree of out tree, which contains root, overall cost of conquering it is not more than M, and amount of oil in vertices is maximal from all situations where above conditions are satisfated.
First idea is that we can make edges [vertice — parent] rather vertices have a cost of conquering, it will not change answer (because every valid subtree, which contains root, covers all paths of type [vertice in subtree — root]. Let vertex 1 have 0 oil and cost of 0.
Now lets make problem recursion-friendy. Suppose we solve next problem : we can have any amount of money from 0 to M in budget, calculate for every 0 ≤ i ≤ M maximum amount of oil that we can conquer using not more, than i money.
If root is only vertex of tree then answer is obviously amount of oil in vertex, repeated from 0 to M. If our tree has at least one edge, we will delete one edge of type [root — vertice], calculate answers for rooted trees with roots in ends of edge we have cut. So now we can combine answer for full tree from answers for subtrees. It can be done in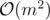 .
.
So now we can solve our problem by solving similar subproblems. There will be at most 2n - 1 recursive calls, because for every recursive call, except ones, which argument is tree with 0 edges, one edge is deleted. So runtime is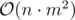 . It still is too slow, but there is one optimisation, which makes solution much faster. You can look my code for it (it is commented, though maybe not completely clearly : 7663770 .
. It still is too slow, but there is one optimisation, which makes solution much faster. You can look my code for it (it is commented, though maybe not completely clearly : 7663770 .
I hope HellKitsune can tell you better solution : he/she has solved this problem at about same time with less problems.
This is the same problem as the one discussed in http://mirror.codeforces.com/blog/entry/13168
I gave an O(nm) solution in the comments there.