Div2A
Alyona is happy when there are no unfinished layers — that is, in front of her is a perfect square with odd side length. Since the order of pieces is fixed, it is enough to keep track of the total current size $$$s$$$ of the puzzle, and after each day check, if the $$$s$$$ is a perfect square of an odd number. The easiest way to do that is to create an additional array containing $$$1^2, 3^2, 5^3, ..., 99^2$$$, and check after each day, whether $$$s$$$ is in this array.
Div2B
Find the character which appears the lowest number of times — if tied, take the earlier character in the alphabet. Find the character which appears the highest number of times — if tied, take the later character in the alphabet. Then, replace any of the lowest-occurrence characters with the highest-occurrence character.
Div2C
We can divide the columns in the matrix into three different groups:
- the columns where we go through the top cell;
- the columns where we go through the bottom cell;
- the columns where we go through both cells.
There should be exactly one column in the $$$3$$$-rd group — this will be the column where we shift from the top row to the bottom row. However, all other columns can be redistributed between groups $$$1$$$ and $$$2$$$ as we want: if we want to put a column into the $$$1$$$-st group, we put it before the column where we go down; otherwise, we put it after the column where we go down. So, we can get any distribution of columns between the $$$1$$$-st and the $$$2$$$-nd group.
Now let's consider the contribution of each column to the answer. Columns from the $$$1$$$-st group add $$$a_{1,i}$$$ to the answer, columns from the $$$2$$$-nd group add $$$a_{2,i}$$$, the column from the $$$3$$$-rd group adds both of these values. So, we can iterate on the index of the column where we go down, take $$$a_{1,i} + a_{2,i}$$$ for it, and take $$$\max(a_{1,j}, a_{2,j})$$$ for every other column. This works in $$$O(n^2)$$$, and under the constraints of the problem, it is enough.
However, it is possible to solve the problem in $$$O(n)$$$. To do so, calculate the sum of $$$\max(a_{1,j}, a_{2,j})$$$ over all columns. Then, if we pick the $$$i$$$-th column as the column where we go down, the answer be equal to this sum, plus $$$\min(a_{1,i}, a_{2,i})$$$, since this will be the only column where we visit both cells.
Div2D
The first idea is to notice, that each element is moved to the back at most once. Indeed, if we fix a subset of elements that we ever move to the back, we can perform the operation once on each of them in any order we like, and that becomes their final order with the smallest possible increase. The optimal order is, of course, the increasing order. The question is how to select this subset of elements to move to the back.
Since we need the lexicographically smallest array, we're looking for some greedy approach that chooses the smallest possible element on the next position one by one, left to right.
- What's the smallest number our resulting array can start with? Of course, the minimum. That means, all the elements in front of the minimum have to be moved to the back and be increased by one.
- What's the smallest number we can have on the second place, given that we have the minimum in the first positions? Either the smallest element to the right of the minimum, or the smallest element among those already moved to the back.
- ...
Analysing this approach, we see that as we go left to right, we keep picking elements from the suffix minima sequence, and keep growing the set of elements we have to move to the right to ''extract'' this sequence from the initial array. At one point, the next smallest element comes not from the suffix minima sequence, but from the pile of integers we move to the right. At this point, all the remaining elements have to be moved to the right once (that is, increased by $$$1$$$), and then listed in sorted order.
So, the answer is always several first elements of the suffix minima sequence, starting from the global minimum, and then all other elements, increased by $$$1$$$ and sorted in increased order. To find the point where we switch from the suffix minima sequence to the moved elements, it is convenient to precomute the minima, and keep a set of those elements we already move to the right.
This solution runs in $$$O(n \log n)$$$, along with many other.
Div1C
First, we will use the idea of binary search on the answer. Let's assume we are currently checking if we can achieve the answer $$$k$$$.
We will iterate over all the necessary coordinates of the vertical lines. To do this, we note that it makes sense to iterate only over those where the lines coincide in the Y-coordinate with at least one of the points. It is obvious that in this case, the necessary vertical lines will be on the order of $$$O(n)$$$.
During the iteration over the vertical line, we will maintain two segment trees for the sum: one for the left half of the plane and the other for the right. $$$t_y$$$ in each of the segment trees will represent how many points have a Y-coordinate of $$$y$$$ in the corresponding half of the plane. In each of the segment trees, we will check if it is possible to divide the half-plane into two parts by a line parallel to the x-axis, so that there are at least $$$k$$$ points in both parts; and if this is possible, we will find the set of suitable lines — it will obviously be some segment $$$[y_{l}, \, y_{r}]$$$. If the intersection of the resulting segments in both segment trees is not empty, then we have found the answer. This can be done by descending the tree in $$$O(\log n)$$$ time.
Thus, the total time complexity of the described solution is $$$O(n \log^2 n)$$$.
Div1D
We will compress the graph into strongly connected components. Inside a component, each runner can move between any pair of vertices and thus visit all. We will now solve the problem for a directed acyclic graph.
We will check for the existence of an answer. Suppose all runners already know the winning plan, and we will try to send them out so that each vertex is visited at least once. To do this, it is necessary to decompose the graph into paths such that:
- each vertex belongs to at least one path;
- no more than $$$a[i]$$$ paths start at each vertex (where $$$a[i]$$$ is the number of runners initially located at the vertex);
- paths may intersect.
Take the source $$$s$$$ and the sink $$$t$$$, and now a path can be represented as a sequence $$$s$$$, $$$u_1$$$, ..., $$$u_k$$$, $$$t$$$.
We will divide $$$u$$$ into $$$u_{in}$$$ and $$$u_{out}$$$ and will consider that a vertex $$$u$$$ belongs to least one transition from $$$u_{in}$$$ to $$$u_{out}$$$. We will draw the following edges:
- from $$$s$$$ to $$$u_{in}$$$ with capacity $$$cap = a[u]$$$;
- from $$$u_{in}$$$ to $$$u_{out}$$$ with $$$cap = inf$$$ and the condition of flow through the edge $$$f \geq 1$$$;
- from $$$u_{out}$$$ to $$$t$$$ with $$$cap = inf$$$;
- from $$$u_{out}$$$ to $$$v_{in}$$$ with $$$cap = inf$$$ for all edges (u, v) in the original graph.
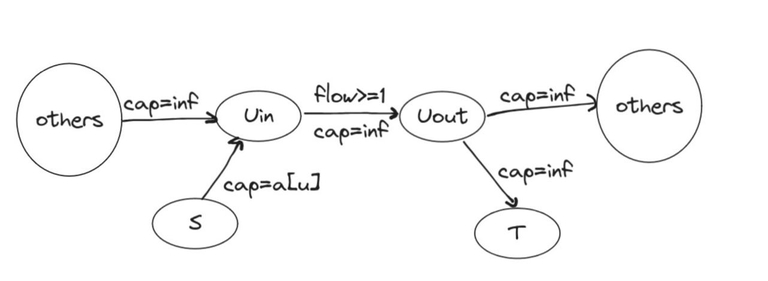This is equivalent to finding a flow with constraints in this graph.
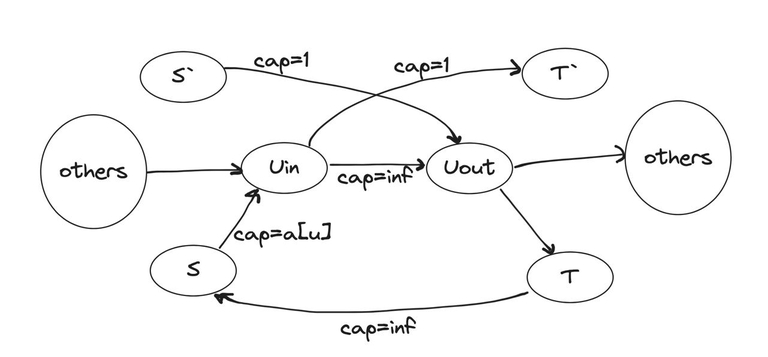
To do this, we will create a dummy source $$$s'$$$ and sink $$$t'$$$, and now for each edge $$$(u_{in}, u_{out})$$$ with flow through it $$$1 \le f \le inf$$$, we will make the following replacements by drawing edges:
- from $$$u_{in}$$$ to $$$u_{out}$$$ with $$$cap = inf - 1$$$;
- from $$$s'$$$ to $$$u_{out}$$$ with $$$cap = 1$$$;
- from $$$u_{in}$$$ to $$$t'$$$ with $$$cap = 1$$$;
- from $$$t$$$ to $$$s$$$ with $$$cap = inf$$$.
Finding a flow that satisfies the constraints is equivalent to finding the maximum flow from $$$s'$$$ to $$$t'$$$, and if it equals the number of vertices, then the answer exists; otherwise, we can output $$$-1$$$ at this step.
Now we minimize the number of runners who initially know the plan. Note that:
- it makes no sense for runners to move until they know the plan;
- it makes no sense to pass the plan to more than one runner from one city.
We try to take this into account when constructing. Instead of adding edges from the source to $$$u_{in}$$$, we will do the following:
- create a vertex $$$u_{cnt}$$$ to control the number of runners and draw edges:
- from $$$s$$$ to $$$u_{cnt}$$$ with $$$cap = a[u]$$$;
- from $$$u_{cnt}$$$ to $$$u_{out}$$$ with $$$cap = a[u]$$$;
- from $$$u_{cnt}$$$ to $$$u_{in}$$$ with $$$cap = 1$$$, $$$cost = 1$$$.
- assign zero cost to all other edges.
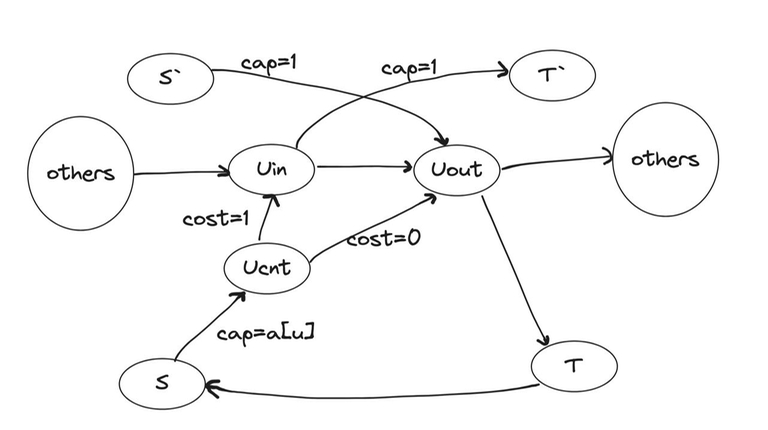This is equivalent to ensuring that all $$$a[i]$$$ runners learn the plan, but if no one comes to our city, we will personally tell exactly one runner from this number, paying $$$cost=1$$$ for that person.
The answer to the problem is the minimum cost of the maximum flow from $$$s'$$$ to $$$t'$$$ with this graph construction. The proof follows from the graph construction.
MCMF can be considered as $$$O(n^2m^2)$$$ or $$$O(n^3m)$$$ for any graphs, but it is worth noting that the flow value $$$f$$$ is limited to $$$n$$$, and we have a solution in $$$O(fnm)$$$ using Ford-Bellman or $$$O(fm\log n)$$$ using Dijkstra's algorithm with potentials.
Interestingly, we note that as a result, we obtained $$$3n$$$ vertices and $$$m + 7n$$$ edges. With careful implementation, MCMF fits well within TL.
Div1E1+E2
For convenience, we will call groups that include certain cities.
The key condition is that each specialization can correspond to no more than one task. Thus, cities from different groups must have "practically sorted" strength values as the group order increases.
Let $$$[l_i, r_i]$$$ denote the segment that includes all the strengths of the cities in group $$$i$$$, where $$$r_i$$$ is the maximum strength of a city from this group, and $$$l_i$$$ is the minimum. If $$$l_i \le r_{i+2}$$$, it is impossible to build a contest, as there must be at least a difference of 2 tasks between the cities corresponding to $$$l_i$$$ and $$$r_{i+2}$$$, but they can differ by at most 1 task in specialization. After this, the problem reduces to considering two neighboring groups and subsequently checking the task difficulties for compliance with the linear conditions of each group.
Let's consider two cases:
If $$$l_i \ge r_{i+1}$$$, it is sufficient to add a few tasks (specifically, just 2) of difficulty from the segment $$$[r_{i+1} + 1, l_i]$$$ to maintain order.
Otherwise, each city in the $$$i$$$-th group that lies in the intersection must solve a task with its specialization. In this case, no task can be in the segment $$$[l_i + 1, r_{i+1}]$$$, as the city with the highest strength in group $$$i+1$$$ will solve at least as many tasks as the weakest city in group $$$i$$$, which we cannot allow. To maintain order with the other groups, it is sufficient to add 2 tasks of difficulty $$$r_{i+1} + 1$$$ (unlike the first case, due to the fact that $$$l_i \le r_{i+2}$$$ cannot occur, we can immediately determine the appropriate task difficulty, but they can be arranged using the same algorithm as for the first case).
It can be noted that when adding pairs of tasks, they need to choose an unused specification (since we are not using it in principle, but otherwise it may cause collisions).
We conclude that we need to arrange tasks with a specified specification that a city from the intersection of groups can solve, meaning its difficulty must not exceed the wisdom of that city, and also arrange 2 tasks of certain difficulties to maintain order between groups. These difficulties arise from possible intersections with other groups when using $$$r_{i+1} + 1$$$ as the task difficulty and possible specification collisions of cities, which may allow a city from a weaker group to solve a task that we did not intend for it, thus violating the strictness conditions between groups.
Most problems cannot arise when $$$m=2$$$, so what has been said above is already a solution (without minor adjustments) to the simple version of the problem.
First, we will solve how to choose the difficulty for tasks with a specific specification. To do this, we will prohibit using the task specification corresponding to cities that form the second case (i.e., from the $$$i+1$$$-th group) with difficulty $$$[l_i, b_j]$$$, where j is the number of such a city. Also, as mentioned, we cannot have a task from the segment $$$[l_i + 1, r_{i+1}]$$$ regardless of the type. To determine the difficulty, it is sufficient to set it to the maximum possible (equal to wisdom) and then gradually decrease it until we reach an allowed difficulty.
To resolve the problem from the first case, we will place barriers with 2 tasks of difficulty equal to the strength of a certain city wherever possible.
If there exists an answer for the given configuration, we will guarantee to construct it this way, using no more than $$$3 \cdot n$$$ tasks. After all calculations, we need to check whether the contest we constructed meets the problem's conditions and output -1 otherwise.
Div1F1
It can be noted that if the string contains the correct number of symbols 'Y', 'D', 'X' and does not have two consecutive identical symbols, then it can be obtained using the given operations.
To demonstrate this, we will provide an algorithm that constructs a sequence of operations leading to the desired string. We will start from the end (from the string we want to obtain to the empty string) gradually removing symbols.
Let's look at the current string. Without loss of generality, let its first symbol be 'Y'. Then the string must contain the substring 'DX' and/or the substring 'XD'. This is true because for the absence of 'DX' and 'XD', it is necessary that between any pair of symbols not equal to 'Y', there is at least one symbol 'Y'. This can be achieved at best by placing 'Y' between every symbol. Thus, the number of symbols not equal to 'Y' with $$$n-1$$$ 'Y' can be at most $$$n$$$. But $$$3n-1>n$$$ when $$$n>0$$$.
Thus, the string has the form 'Y...ADXB...'.
If A $$$\neq$$$ B, we can remove the symbols 'Y', 'D', 'X' and nothing will break.
If A = B, then A = B = 'Y', since A != 'D' and A != 'X'.
Then the string has the form 'Y...YDXY...', and we can remove the substring 'YDX' and still have an unbroken string 'Y...Y...'.
Div1F2
We will isolate substrings from the string that consist entirely of '?'. For each, we will denote its length as $$$len_i$$$ and the two neighboring symbols (standing to the left and right) as $$$l_i$$$, $$$r_i$$$. (If the right and/or left symbol is absent, we will take it as '#', a symbol that does not match any of our interests).
We will write trivial constraints on the number of available symbols of each type on the segment. It is obvious that the number of symbols of each type cannot exceed $$$\frac{len_i+1}{2}$$$: we will place one symbol for every other symbol. But if, for example, we had a symbol 'Y' on the left, the number of positions where we can place 'Y' decreases by $$$1$$$. In total, we can place no more than $$$\frac{len+1-(l_i=b)-(r_i=b)}{2}$$$ symbols of type b. We will write such constraints for each type of symbol and denote them as $$$Y, D, X$$$ respectively.
It turns out that we can arrange $$$y$$$ symbols 'Y', $$$d$$$ symbols 'D' and $$$x$$$ symbols 'X' if and only if $$$y+d+x=len_i$$$ and $$$0\leq y \leq Y, 0 \leq d \leq D, 0 \leq x \leq X$$$. This can be proven by induction or checked with stress tests on small values. From this, we conclude that in order to be able to arrange $$$x, d, y$$$ symbols of each type, the inequalities above must hold.
From the equality $$$y+d+x=len_i$$$, we express $$$d=len_i - (x+y)$$$.
This results in three constraints: $$$0\leq x \leq X, 0 \leq y \leq Y, 0 \leq len_i - (x+y) \leq D$$$. The first two form a rectangle, and the third cuts off two corners at a $$$45$$$ degree angle. This is a convex polygon.
Thus, if for each segment of '?' we write a polygon and sum them using Minkowski sum, we will obtain constraints for the entire string.
Since in the Minkowski sum (after merging collinear consecutive segments) there will be at most 6 points, we can write a greedy algorithm that sequentially tries to match the required symbol to each '?'.
The final asymptotic complexity is $$$O(n)$$$ with some constant.
Comments (0)
