Subsequences: they’re like the wardrobe combinations of coding—every possible way to arrange your elements without messing up the order. A subsequence is any sequence derived by deleting some (or no) elements of the array without changing the order of the remaining elements. This is my first blog on Codeforces ^-^ In this blog, I’ll guide you through the process of generating all subsequences of a given array using recursion. Along the way, we’ll explore the logic, implementation, and common pitfalls, with just the right mix of fun and formality.
What Are Subsequences?
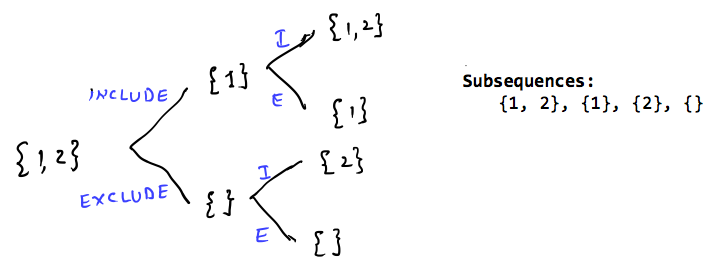
A subsequence is any sequence derived from an array by deleting some (or no) elements, without changing the order of the remaining elements.
For example, given the array [1, 2, 3], the subsequences are: [], [1], [2], [3], [1, 2], [1, 3], [2, 3], [1, 2, 3] Notice how the order is preserved, and yes, the empty set [] is part of the deal—because sometimes doing nothing is a valid choice. :P
The Recursive Approach
Recursion is basically your lazy friend—it works by delegating smaller parts of the problem to itself. For subsequences, here’s the plan:
- At every index, you have two choices: — Pick the element: Include it in the current subsequence. — Don’t pick the element: Skip it and move forward.
- Keep repeating this until you’ve processed all elements.
- At the end, print (or store) the current subsequence.
Visualizing the Recursion Tree
For the array [1, 2, 3], the recursion tree looks like this:
[]
/ \
[1] []
/ \ / \
[1,2] [1] [2] []
/ \ / \ / \ / \
[1,2,3] [1,2] [1,3] [1] [2,3] [2] [3] []
- At the root: Start with the empty set
[]. - First level: For each element, decide whether to pick or not pick it.
- Second level: Repeat the same decision for the next element.
- Third level: Continue until all elements are processed.
- Leaf nodes: Represent the final subsequences.
By the time the recursion is complete, you’ll have all possible subsequences.
Code Implementation
Here’s how to bring this concept to life with C++:
#include <iostream>
#include <vector>
using namespace std;
void generateSubsequences(int idx, int arr[], int n, vector<int> &ds) {
// Base case: If we’ve processed all elements
if (idx == n) {
if (ds.empty()) {
cout << "{}"; // Represent the empty subsequence
} else {
for (auto it : ds) {
cout << it << " ";
}
}
cout << endl;
return;
}
// Pick the current element
ds.push_back(arr[idx]);
generateSubsequences(idx + 1, arr, n, ds);
// Don’t pick the current element (backtrack)
ds.pop_back();
generateSubsequences(idx + 1, arr, n, ds);
}
int main() {
int arr[] = {1, 2, 3};
int n = sizeof(arr) / sizeof(arr[0]); // Size of the array
vector<int> ds; // To store the current subsequence, we are passing this data structure (ds)
generateSubsequences(0, arr, n, ds);
return 0;
}
How It Works
Let’s run this on the array [1, 2, 3]: 1. Start with Index 0 (1): — Pick 1 → Add 1 to the current subsequence and move forward. — Don’t Pick 1 → Skip 1 and move forward.
Move to Index 1 (
2): — For both cases from the previous step: — Pick2→ Add2to the subsequence. — Don’t Pick2→ Skip2.Move to Index 2 (
3): — Again, pick or skip3for each branch.
By the time you reach the base case (idx == n), all possible subsequences will be printed.
Output
For the input arr = [1, 2, 3], the output will be: 1 2 3 1 2 1 3 1 2 3 2 3 {}
Common Mistakes (and How to Avoid Them)
- Forgetting to Backtrack: If you don’t
pop_back()after picking an element, your subsequences will contain extra elements from previous recursive calls. Backtracking ensures each branch of the tree starts fresh. - No Base Case: Without the base case (
idx == n), your recursion will run forever and probably crash harder than your first Codeforces contest. >-< - Printing Inside Loops: Make sure to print subsequences only after reaching the base case.
>>
Try modifying this code to:
Count the number of subsequences.
Store the subsequences in a 2D vector instead of printing them directly...
Feel free to share your thoughts or questions below. Happy coding! :D











I don't want to end up as rude but, how is this useful and isn't this trivial?
I suppose OP wants some contribution points.
it's basic coding of complete search, not something unique
world's most chatgpt blog ever
Even though people might find this as a "Basic" or "Anyone could have googled this" blog. But for me it kinda makes sense tho...
ofc it's not as advanced as you want to see in a CP website's blog. But you cant deny that content like this belongs to CF. (making CF more newbie friendly).
can this be modified for contiguous subsequences?