Hello fellow problem-solvers. I am writing this post to ask a doubt I am not able to munch anymore. The problem is Double Sum 3 which came as problem F on Atcoder Beginner Contest 390. I am interested to know the knowledge gaps and thoughts which are preventing me from solving this. I don't just need the solution I want if I ever came across a situation remotely matching this, I am at least able to self realize it if not solve it.
My thoughts:
Given the relation ΣNL=1ΣNR=Lf(L,R), I was not able to come up with anything linear. So I did what is most obvious to me, created a graph out of the problem. Given the test case, I made a graph:
5
3 1 4 2 4
Now in this, starting from 3, if adding values is taken into a group, its contribution is 0 otherwise it forms a group of its own and its contribution is 1. Each value say arr[i] have an edge to arr[i], arr[i-1] and arr[i+1] because if anyone of these are present then no new component is formed. So this is the final graph: 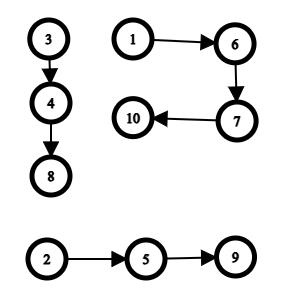
There are 3 disconnected components so the answer for F(1,10) is 3
The contribution of each index:
[1,1,1,0,0,0,0,0,0,0]
If a node is added and it reduces the number of components like [1,2] [4,5] and we add 3 then its contribution is -1 because it reduces our answer.
So now for F(1,3) the answer is 3; F(1,5) the answer is 3 So for ΣNi=1F(i,N) the answer is the sum of the array contribution across all. For this, across all these are the contributions:
[10,9,8,0,0,0,0,0,0,0] so the sum of all contributions is 27 and the answer for ΣNi=1F(i,N) is 27
Now I thought, start from index 1 and start removing the nodes and their contributions and then just sum it as usual. If my sum function is G(start,N) then I can go from ΣNi=1G(i,N) so remove the contribution of each index and add it to the sum and I got a net sum the answer.
Removing 1, makes all of its children now to form individual groups and they now contribute +1 more than their usual value. And we can just compute all G(i,N).
This logic passes all samples and permutation on Atcoder but failed on random tests here.
My code fails for this test case I found after stress-testing:
10
4 1 3 5 2 1 2 5 6 4
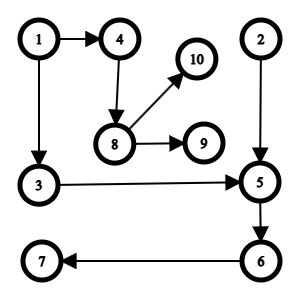
Now why this fails? The contribution of node at index 10 will become -1 after removing node at index 1 because its children are still connected by this index shown in the graph below. Now I can run an algorithm to find if the children as still connected by a bridge vertex find that bridge and decrease its value but this seems too much. What am I missing?
I don't know if this happens to higher rated or more extensive problem-solvers or not but I don't want to keep doing this more than this. I used a DSU and a lot of conditions in code which is readable and good but it seems too complex for a solution.











Guys any help on this please.
One of the strategies I follow for this kind of counting problem is see how much each individual number contributes to the asked value. For example, consider a sequence A_L, …, A_R. How much does a given A_i contribute to f(L,R)? If (A_i — 1) is not in the sequence then A_i is the smallest l of some choice (l,r) contributing +1 to f(L,R), otherwise it does not contribute, because we can extend A_i — 1 to also erase it. Then for each number A_i for i in [1,n] we count how many f(L,R) it contributes. That is, for each i we get the first index j to the left of i such that A_j = A_i — 1 and similarly we find the first index k to the right. Then each A_i contributes (i-j-1)*(k-i-1) to the final answer.
Other strategy I use for those kind of problems is counting the complement, although this strategy does not help for this specific problem I think.
Worked. Thanks.