ADJA's blog

Palindromic tree
By ADJA, 10 years ago, In English

New data structure for solving problems involving palindromes in the strings:
http://adilet.org/blog/25-09-14/

Thanks to droptable for sharing it!

  • Vote: I like it
  • +118
  • Vote: I do not like it

»
10 years ago, # |
← Rev. 3   Vote: I like it -22 Vote: I do not like it

It looks like manachers palindrome algorithm. It also works in O(N). I mean it uses the same logic. I dont say that they are completely the same.

→ Reply
»
10 years ago, # |
← Rev. 6   Vote: I like it -13 Vote: I do not like it

What about implementation ?

→ Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

This algorithms complexity is guaranteed O(n) or generally O(n). I learn algorithm but I don't understand algorithms complexity. My opinion this algorithms complexity maybe O(n*log(n)).

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I think , it is guaranteed O(n) , cause left side of 't' is always pointing to a index less than or equal to the index being added (x) & its always increasing , so it will need at most n iteration .

    → Reply
»
10 years ago, # |
← Rev. 3   Vote: I like it -8 Vote: I do not like it

For part of article that says: 'a string of length n can have at most n palindromic substrings'. Is the following how you prove it?

Pf. Worst case is characters are all different, in which case there are exactly n palindromes each of size 1. Other case is when there are at least two similar characters: suppose that string looks like **ya****ax*** where x != y. Suppose that a****ais a palindrome, so there are length(a****a)/2 palindromes in that substring. So if remaining letters are all distinct, string has: length(a****a)/2 + n - length(a****a)/2 = n palindromes.

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +8 Vote: I do not like it

    well, I didn't try to understand your proof. One easy way to prove it:

    See on the all of palindromes that ends on position i, all except largest of them appeared before (because they are also prefixes of the largest one). So adding 1 letter adds at most one new palindrome.

    → Reply
»
10 years ago, # |
  Vote: I like it +8 Vote: I do not like it

Problems recommanded:

HDOJ 3948: The Number of Palindromes

CERC14 G: Virus synthesis

Xi'an14 G: The Problem to Slow Down You

→ Reply
»
10 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

A part of the article says: "The string xAx is the only palindrome substring of p + x, that we possibly never saw in p. To understand why this is so, notice that all new palindrome substrings which we didn't meet in p must end on that last letter x, and therefore be the suffix-palindromes of p + x. Because xAx is the largest suffix-palindrome of p + x, all other smaller suffix-palindromes of it can be found in some prefix of xAx (since for any suffix of the palindrome there is a corresponding similar prefix), and therefore we alreay saw them in p". What is the meaning of this part ?

→ Reply
  • »
    »
    10 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    This part tries to tell U every time we add a letter, the number of new palindrome may increase by one or not.

    It's easy to understand since xAx is the largest suffix palindrome and if there was a new palindrome it must be ended with the letter we added now. And since xAx is the largest suffix palindrome, this new palindrome's left bound will be in the range of xAx. But if a substring Bx is a palindrome, and the left bound of B is less than xAx, we know xB'(B' is the reverse of B) is also a palindrome, and it appears in the left part of xAx, and not ended with right x. So it has appeared. So xAx is the only substring which may be a new palindrome.

    → Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I just got a nice question regarding palindromic tree in my blog

Question (if I got it right): can we produce the same arrays as Manacher's algorithm does — i.e, largest odd/even palindrome with a middle in this position — using palindromic tree?

I didn't come up with an answer right away, so do you know how to do this? You can write it here or in the blog.

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    We can. But I don't know any way to calculate it easier or faster than in Manacher's algo. The most obvious way is bin search + check if [l..r] is a palindrome. .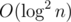

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Hi, thanks for an answer. How would you check that substring in [l..r] is palindrome using palindromic tree?

      → Reply
»
9 years ago, # |
  Vote: I like it +1 Vote: I do not like it

Palindromic tree problems: 1) http://www.spoj.com/problems/NUMOFPAL 2) http://www.spoj.com/problems/LPS

→ Reply