Following are unofficial solutions for all problems.
100499A - Cool number
Solution 1
The most obvious solution for this problem is to brute force all numbers, and check if it is a cool number. My code
After running this code for several minutes, you should be able to get results for all K ≤ 9. The only result for K = 7 is 3211000, for K = 8 is 42101000 and for K = 9 is 521001000. From these results, you should be able to guess the result for K = 10 is 6210001000.
Solution 2
There are many ways to optimize the above solution. The most standard way is to see that the sum of all digits is equal to K, thus if you restrict your brute force to exit when sum of digit is greater than K, you should get a solution which runs in around a few seconds.
100499B - K smallest numbers
Since all numbers are at most 107, you can count number of occurrence of each value.
100499C - Grid city
I don't know how to solve this problem, but following are some ideas from tester:
For each query, (x1, y1) to (x2, y2), consider following lines:
- Nearest North lines from (x1, y1) and (x2, y2)
- Nearest South lines from (x1, y1) and (x2, y2)
- Nearest East lines from (x1, y1) and (x2, y2)
- Nearest West lines from (x1, y1) and (x2, y2)
So we have 8 lines from (x1, y1) and 8 lines from (x2, y2). Consider all intersections of these lines (there are 64 of them). Then we can use Floyd to find shortest path in this new grid.
This problem has many implementation details that need to be taken care of, for example, the points in queries can be on locations that are not intersections.
Accepted code from yenthanh.t7 who implemented this idea.
100499D - Pairwise Coprime Set
To solve this problem, you must observe that the solution is always the set of primes less than or equal to N. This can be proved mathematically, but you can also observe this from playing with small cases.
To find all primes that is at most N, you can use Sieve of Eratosthenes.
100499E - Binary Search Tree
Disclaimer: I haven't coded this problem, so not sure the following will work correctly.
Since a connected component of a binary tree is also a binary tree, the only necessary condition for it to be a binary search tree is that the keys should be in increasing order.
We write a method dfs(Node u) that returns the maximum binary search tree rooted at node u. The outline of the algorithm looks like following:
Tree dfs(Node u) {
Tree left = dfs(left_child(u))
Tree right = dfs(right_child(u))
return build_result(left, right)
}
There are still two things that need to be taken care of:
How to represent a tree efficiently? Since we know that it is always a binary tree, and only the order is important, you can represent it with an array of integers, containing the keys of the tree.
How to build result for Node u from result of its left child and right child? To contain node u, we can only use nodes in left subtree having keys less than node u. Similarly, we can only use nodes in right subtree that have keys greater than node u. So, from the result of left subtree, we remove all nodes that have keys greater or equal to node u. Similar for right subtree, and then we can combine these keys to get the result for node u.
Now, we have something that can run in O(N2). To optimize it to O(N * logN), you can do the following:
When you get the 2 arrays from left subtree and right subtree, reuse the bigger one (adding necessary values to the other one, and return that array)
Code from team ThanQ+: here.
100499F - Tree again
Let's look closely at the pre-order traversal of the tree. You can see that for every subtree rooted at vertex u, all of its nodes are at adjacent positions! Using this information, the queries become:
Maintain the pre-order traversal of the tree
For query type 1, cut the segment of the pre-order traversal of sub-tree u, and put it after pre-order traversal of sub-tree v.
For query type 2, print the i-th node in the pre-order traversal.
Thus, the main idea is to use a balanced binary search tree, such as splay tree to maintain this pre-order traversal. However, there are still some implementation details that need to be take care of: For query 1 to work, you must also maintain the end-point of pre-order traversal of each subtree. This turns out to be very hard to implement.
A trick to work around this is to modify the pre-order traversal a bit: We add each vertex twice, one when entering the pre_order_traversal method, one before exiting the pre_order_traversal method. With this, you can easily maintain the end-point of pre-order traversal of each subtree, but query 2 needs some modification to work.
You can see my code for more details.
100499G - Visual Illusion
This is the most simple problem in the constest. You just need to print the board as shown in the problem statement.
Code from team ThanQ+
100499H - CCTV
Idea:
Consider only camera 1, located at (0, 0). Divide the room into smaller triangles. For each triangle, the area that is visible from camera 1 should also be a triangle.
The most difficult part in this problem is how to divide the room into smaller triangles. One way is to sort all corners of glass cases in clockwise order. Let's call these points P1, P2, ..., Pk. Now consider triangle formed by 2 rays: (0, 0) — Pi and (0, 0) — P(i + 1). The viewable area of this triangle is also a triangle. Thus, you only need to consider all edges of glass cases, and see which edge is closest to the camera.
100499I - Fraction
Some observation:
- 0.12345 = 12345 / 100000
- 0.(123) = 123 / 999
- 0.0(123) = 123 / 9990
So, to solve this problem, you need to split the number into three parts: Integer, fraction and repeated fraction. Then add these parts together. When add these fractions together, you must be careful to avoid overflow. One way to be sure is to use Java BigInteger.
100499J - Healthy Recipes
This is a knapsack problem, which can be solved using dynamic programming. However, there is one small trick in this problem: The number of meals can be exponential, and thus in the dp function, you need to reset the dp value to K when it exceeds K. See author solution for more details.











can you give me all of the test of this contest?
No.
on E:
you gotta be kitten. The most important parts are missing :D. useless.
I added some details. Is it good now?
What an unbelievable simple solution in problem C!
Can you please check if I misunderstood something? I don't believe the solution for E is correct.
However, consider the following subtree:
Node A has value 3 and left child B
Node B has value 1 and right child C
Node C has value 4 and left child D
Node D has value 2 and no children.
The best BST rooted at B is to keep all the nodes (B,C,D). Let's call this BST T. If we follow the solution described above, to compute best BST for A, we remove all nodes from T with keys greater or equal to 3, so we remove node C. This means our BST for A contains (A,B,D). However, this is not a connected tree.
Is there some other thing that needs to be done here?
Yes, when you remove a node, you must also remove its children. This can be done by, for example, keeping track of the first and last positions of a node's children.
I haven't coded this problem, so I may be wrong though.
For problem A: let xi be the number of digit i, we have
and since $k \leq 10$, this function have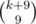 solution which is small 220, we can try all of them and you know the number of each digit, you get the number, it's easy to check if it's ok and the time complexity is about O(2k * k).
solution which is small 220, we can try all of them and you know the number of each digit, you get the number, it's easy to check if it's ok and the time complexity is about O(2k * k).
E could be solved in O(N) (if my analysis is correct).
I used a similar dp approach in the editorial. For each node, after calculating the maximal tree size for its two children, I combine those two answers by removing nodes that are inappropriate from both subtrees.
This removing step is O(N) in total if we only consider the nodes that are still present in the two children. Because every node is added and removed at most once. Therefore if we maintain an array which marks which nodes are still present this removal will take O(N) at most.
How do we know which nodes are inappropriate. We traverse down the left most path of the right child and the rightmost path of the left child. This traversal will also take O(N) in total.
Btw, why am I keep getting this when viewing the problems of the contest: