Given a Mincost Maxflow problem where all costs are non-negative integers at most K, for some small values of K (K = 1, 2, 3...)
I've heard the following claim: There is ALWAYS a conversion from this Mincost Maxflow problem to a Maxflow problem. Is this claim true? If yes, then I think it is very valuable in competitions.











Well if K is small then you can generally profit by finding a shortest path in a graph in O(V + E + K). While this isn't a reduction to MaxFlow, it does bring your time complexity to something similar.
How? Oo
Split each edge into Ki edges with cost 1 and run bfs.
It is O(V + E * K), isn't it? Also what to do on next iterations?..
Edit: wrong, of course
Something like O(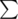 K). Not sure if I understand your question. You do the same thing on each iteration, just as you would in Min-Cost Flow with Bellman-Ford or with Dijkstra + potentials.
K). Not sure if I understand your question. You do the same thing on each iteration, just as you would in Min-Cost Flow with Bellman-Ford or with Dijkstra + potentials.
In the end, each part of the initially divided edge will be filled with the same amount of flow, so it will be easy to get back to the original graph.
klamathix saying about O(V + E + K), but your solution is O(V + E * K). Actually we can make first iteration in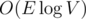 with a simple Dijkstra in this case, so...
with a simple Dijkstra in this case, so...
Question is, what it K? Since each edge has different cost. And the solution above is wrong anyway, sorry!
Maximum cost.
And then in residual graph we will have edges with -1 cost , how can you run BFS in this case?
I'm an idiot :<
I see. But there are many Max flow algorithm that is not based on finding augmenting path and are much faster, so even with this trick, Min cost is still much slower.
UPD: and as mentioned, in residual graph, there are negative edges. How to deal with that? :)