MikeMirzayanov's blog

Codeforces Round #277.5 (Div. 2) Editorial [A-D for now]
By MikeMirzayanov, 10 years ago, In English

489A - SwapSort

All you need is to swap the current minimum with the i-th element each time. You can do it with the code like:

    for (int i = 0; i < n; i++)
    {
        int j = i;
        for (int t = i; t < n; t++)
            if (a[j] > a[t])
                j = t;
        if (i != j)
            answer.push_back(make_pair(i, j));
        swap(a[i], a[j]);
    }

This solution makes at most n-1 swap operation. Also if (i != j) is not necessary.

489B - Бал в БерлГУ

There are about 100500 ways to solve the problem. You can find maximal matching in a bipartite graph boys-girls, write dynamic programming or just use greedy approach.

Let's sort boys and girls by skill. If boy with lowest skill can be matched, it is good idea to match him. It can't reduce answer size. Use girl with lowest skill to match. So you can use code like:

sort(boys.begin(), boys.end());
sort(girls.begin(), girls.end());

for (int i = 0; i < n; i++)
    for (int j = 0; j < m; j++)
        if (abs(boys[i] - girls[j]) <= 1)
        {
            girls[j] = 1000;
            result++;
            break;
        }

489C - Даны длина и сумма цифр...

There is a greedy approach to solve the problem. Just try first digit from lower values to higher (in subtask to minimize number) and check if it is possible to construct a tail in such a way that it satisfies rule about length/sum. You can use a function `can(m,s)' that answers if it is possible to construct a sequence of length m with the sum of digits s:

bool can(int m, int s)
{
    return s >= 0 && s <= 9 * m;
}

Using the function can(m,s) you can easily pick up answer digit-by-digit. For the first part of problem (to minimize number) this part of code is:

    int sum = s;
    for (int i = 0; i < m; i++)
        for (int d = 0; d < 10; d++)
            if ((i > 0 || d > 0 || (m == 1 && d == 0)) && can(m - i - 1, sum - d))
            {
                minn += char('0' + d);
                sum -= d;
                break;
            }

The equation (i > 0 || d > 0 || (m == 1 && d == 0)) is needed to be careful with leading zeroes.

489D - Невыносимая запутанность бытия

Let's iterate through all combinations of a and c just two simple nested loops in O(n2) and find all candidates for b and d inside. To find candidates you can go through all neighbors of a and check that they are neighbors of c. Among all the candidates you should choose two junctions as b and d. So just use https://en.wikipedia.org/wiki/Combination All you need is to add to the answer 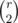, where r is the number of candidates (common neighbors of a and c). The code is:

    for (int a = 0; a < n; a++)
        for (int c = 0; c < n; c++)
            if (a != c)
            {
                int r = 0;
                for (int b = 0; b < nxt[a].size(); b++)
                    if (nxt[a][b] != a && nxt[a][b] != c && g[nxt[a][b]][c])
                        r++;
                result += r * (r - 1) / 2;
            }

It is easy to see that the total complexity is O(nm), because of sum of number of neighbors over all junctions is exactly m.

P.S. I'll be grateful if some of you will write editorial of E and F in comments because of now I should leave Codeforces and will return back some hours later. Thank you for participation!

  • Vote: I like it
  • +114
  • Vote: I do not like it

Comments Comments (62)
| Write comment?
»
10 years ago, # |
  Vote: I like it +20 Vote: I do not like it

very nice problem in this round,very thanks MikeMirzayanov :)

→ Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I needed just 2 minutes for problem D T_T

→ Reply
»
10 years ago, # |
  Vote: I like it +13 Vote: I do not like it

My solution 8732482 of D.
I use this fact:
If A is adjacency matrix and B = A ^ k then number of different path whits length = k from u to v = B[u][v]

Also i speed up matrix multiplication using fact that we have only m '1' in matrix.

→ Reply
»
10 years ago, # |
  Vote: I like it +6 Vote: I do not like it

Problem D:

Start a small ( just 2 steps ) dfs ( or bfs ) from each graph vertex, count the number of ways to get from current vertex in some other ( let it be cnt[v] ). Then add cnt[v] * ( cnt[v] - 1 ) / 2 to the answer.

My Code

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Hello! Very nice approach to the problem. I just couldn't get why do you used the combination! Could you explain me that?

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it +5 Vote: I do not like it

      Suppose that we get 3 ways of reaching a vertex X now suppose they are:

      A -> B -> X A -> C -> X A -> D -> X

      now we need to select 2 of the given 3 paths to make a rhombus ie BC or CD or BD, so total rhombus are nC2 , where n is the number of ways of reaching the vertex in one dfs (after 2 steps)

      → Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    your "used" array is useless.

    → Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

For problem D:

I went through all the nodes, and for each node, I choose 2 of its neighbors (I try them all), then add to the sum the common neighbors of those 2.

My Code

→ Reply
»
10 years ago, # |
  Vote: I like it +7 Vote: I do not like it

Here is my editorial for F:

The state of the board can be stored with three variables: The row we're on, the number of columns which have no 1s in them (call it x), and the number of columns with exactly one 1 in them (call it y). We then have the following options, depending on these counts.

For each row, we need to select two indexes to be 1s, the rest need to be zero. Here are the possible ways to do that. If x > 1, there are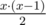 ways to choose two columns to insert a 1. This decreases x by two and increments y by 2.

If x ≥ 1 and y ≥ 1, then there are x·y ways to choose the two columns.

If y > 1, then there are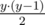 ways to choose the two columns to insert a 1. This decreases y by 2.

Combining all of these methods together yields the right answer.

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    youll need to save memory for row number when using dp

    → Reply
  • »
    »
    10 years ago, # ^ |
    ← Rev. 2   Vote: I like it +8 Vote: I do not like it

    During the contest I came up with a similar idea.(didn't submit...), but stuck with stupid thoughts T_T. So the dp should be something like: dp[line][x][y], which means at current line, after I have put 1's, when I now have x columns containing no 1s and y columns containing one 1, how many possible ways can I place 1's as the matrix from line 1 to current line.

    And current state will have effect to dp[line+1][x-2][y+2](I choose 2 no-1-columns), dp[line+1][x][y-2](I choose 2 one-1-columns), dp[line+1][x-1][y](I choose 1 one-1-column and 1 no-1-columns). This is describled by arknave.

    The result will be dp[n][0][0] since each column should contain exactly 2 ones.

    And for each line, we have to calculate all the status derived from last line, so the time complexity should be O(m*n^2).

    Here is my solution. 8740822

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Oops, O(n^3)

      → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
          Vote: I like it +16 Vote: I do not like it

        You can reduce that to O(n^2). My O(n^3) got TLE.

        Notice that you don't actually need to maintain a parameter for row. You can calculate what row you are at from number of zero-columns and one-columns you have. If you have 3 zero columns and 2 one columns, that means you have to put 3*2 + 1*2 = 8 one's inside the matrix still. That means, 8/2=4 rows have not been determined yet.

        Just remove row from memoization and solution becomes O(n^2). My Submission: 8737649

        → Reply
        • »
          »
          »
          »
          »
          10 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          You can also use a queue or sth else to maintain the actual states for the O(n^3) dp. It will reduce the complexity of your dp to n^2.

          → Reply
        • »
          »
          »
          »
          »
          9 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          Didn't realize that. Thanks a lot :)

          → Reply
  • »
    »
    10 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    why haven't we taken the case of selecting both from the no 1s or both from both one 1s in the case of x>=1 and y>=1 thus adding (x*(x-1))/2 and (y*(y-1))/2 to x.y?

    EDIT:Got it

    → Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

wait for F solution

→ Reply
  • »
    »
    10 years ago, # ^ |
    ← Rev. 2   Vote: I like it +3 Vote: I do not like it

    I use dp to solve pF. You can count the number of ones in each column, than you could use [500][500] to dp. If the first represent how many columns have 0 one, and the second means 1 one. Than you can use dp.

    for i,j:
  [i-2][j+2] += [i][j] * C(i,2)
  [i-1][j-1+1] += [i][j] * C(i,1)*C(j,1)
  [i][j-2] += [i][j] * C(j,2)

    And the answer is all columns have 2 ones (ans=[0][0])

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it +5 Vote: I do not like it

      Thank you, bro, it's a good solution!

      → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      e....it looks like you made a small mistake: [i][j] += [i — 2][j + 2] * C(i, 2); [i][j] += ... [i][j] += ...

      → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it 
        [i-2][j+2] += [i][j] * C(i,2)

        means we choose two in i columns who have 0 one to two columns who have 1 one.

        And this is the same:

        [i][j]+=[i+2][j-2]*C(i+2,2)
[i][j]+=...

        It have many ways to get the answer, you can choose your way.

        → Reply
»
10 years ago, # |
  Vote: I like it +58 Vote: I do not like it

Solution for E: The idea is to binary search for the best ratio. So now, this problem reduces to checking if a certain ratio is possible. Let K be the optimal ratio.

First, add a dummy node at x=0, and between every pair of nodes with x_i < x_j, add an edge with cost sqrt(|x_j-x_i-L|) — R * b_j. We will now show that if the shortest path from x=0 to x_n is negative, then we have (sum of frustrations) — R * (sum of picturesqueness) < 0, so (sum of frustrations) / (sum of picturesquness) < R. We know that K <= (sum of frustrations) / (sum of picturesquness), thus, we get that R > K. On the other hand, if the shortest path is positive, then this implies R < K. Thus, we can binary search for the optimal K. Once we've found K, we can then just do the standard dp while keeping prev pointers to reconstruct the path.

→ Reply
  • »
    »
    10 years ago, # ^ |
    ← Rev. 3   Vote: I like it +19 Vote: I do not like it

    I have a question. If (sum of frustrations) — R * (sum of picturesqueness) < 0 then R > (sum of frustrations) / (sum of picturesquness) > K leads to R > K. But if (sum of frustrations) — R * (sum of picturesqueness) > 0 then R < (sum of frustrations) / (sum of picturesquness), i cant find out why this leads to R < K.

    EDIT : I have found out why that leads to R < K. Tks for a nice solution :)

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Why it leads to R<K ? Would you please explain .

      → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
        ← Rev. 2   Vote: I like it +3 Vote: I do not like it

        Let f be the sum of frustrations, p be the sum of picturesqueness. When the shortest path is positive => all path from x1 to xn is positive => f — R*p is positive for all f and all p => with EVERY pair of f and p we have f/p > R => K > R.

        → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
        ← Rev. 4   Vote: I like it 0 Vote: I do not like it

        (a1+a2)/(b1+b2) = R

        (a1+a2) -R*(b1+b2) = 0 // if and only if R is the answer

        → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      What is the meaning of shortest path in this question?

      → Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Since we did a binary search, we can only check down to a certain finitely small resolution of the ratio. How can we be sure that there does not exist another answer which actually has a better ratio, but due to our resolution in binary search, was ignored? Plus, I think since the problem deals with real number, there should be a limit on the resolution of the answer. For example, if the optimal ratio is 1.000001, the solution which yields 1.000002 should also be correct. Or maybe in this case, we can; with the given constraints; prove that two solutions must differ by at least some value.

    → Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Some other similar problems: http://poj.org/problem?id=2728 http://poj.org/problem?id=3621

    → Reply
  • »
    »
    10 years ago, # ^ |
    ← Rev. 3   Vote: I like it 0 Vote: I do not like it

    .

    → Reply
  • »
    »
    10 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    Good tutorial

    → Reply
  • »
    »
    5 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Nice Idea. We could somehow deal with fractions as one value whose optimal can be found out easily with dynamic programming (shortest paths).

    I have one doubt in its implementation. How do we decide the needed precision for binary search in such problems ? Or do we just keep it very low, but not low enough for Time Limit to be issue.

    → Reply
  • »
    »
    5 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Excellent idea. Thanks for sharing!

    → Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Editorial for D: What i did is a DFS but checking whether a edge is visted or not if edge is not visted. if(edge is visted ) i do nothing else what i do is dfs(current parent) and before entering the dfs i upadte all paths from let say parent to child(current) Link for Solution: Solution

→ Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

My solution for D is to iterate through every possible start and stop point (a and d) and then calculate the number of b and c respectively. I made a mistake that in the O(n^2) loop, i used the memset() function to memset an O(n) array. Expected to be O(n^3) but still AC. Could anyone explain? The link to my code is below http://mirror.codeforces.com/contest/489/submission/8728972

→ Reply
»
10 years ago, # |
← Rev. 3   Vote: I like it 0 Vote: I do not like it

It's a nice Round ! That helps me get more than 300 ratings ! Thanks for MikeMirzayanov !

→ Reply
»
10 years ago, # |
← Rev. 2   Vote: I like it +3 Vote: I do not like it

Life of real man according to MikeMirzayanov

for (int i = 0; i < n; i++)
    for (int j = 0; j < m; j++)
        if( ... )
        {
            girls[j] = 1000;
            result++;
            break;
        }

- live in O(nm), be a man

→ Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Would someone mind to share the DP solution for problem B? :)

→ Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can anybody tell me why this code is giving TLE ??

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    most O(n^3) solution for C got TLE because of strict time limit. The mod function take more time than + — * and /.

    You can reduce it to O(n^2) by the fact that remain_row=2*(no_of_zero)+(no_of_one)

    → Reply
»
10 years ago, # |
← Rev. 3   Vote: I like it 0 Vote: I do not like it

Can someone explain why the complexity is O(mn) and not O(n^2 m) At least the j++ in the second loop does get executed n^2 times. So how can we give the argument that the second loop is only executed m times?

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it 
    for (int b = 0; b < nxt[a].size(); b++)

    this only enumerate all adjacent vertices of 'a' there are degree(a) 'b's

    O(n*n*Sigma_a(deg(a))) =O(n*m)

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I think O(n*n + Signma_a(deg(a)) ) == O(n*n + m) at max.. Correct me if i am wrong. How will O(n*n*Sigma_a(deg(a))) make O(n*m)

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
        ← Rev. 2   Vote: I like it 0 Vote: I do not like it

        Each node is accessed only n times and whenever a node is accessed loop runs for deg(a) times.

        consider outer loop to be loop of reference starting points for 'damn rhombi'.

        consider 1st inner loop to be ending point. Now 1st inner loop runs for O(n).

        Now, 2nd inner loop that finds candidates run for O(deg(a)).

        Hence, total complexity would be O(sum_over_all_a(n*deg(a))).

        this would be O(2*n*m)=O(n*m).

        If you want to implement this solution you would need to make both adjacency matrix as well as adjacency list.

        → Reply
»
10 years ago, # |
  Vote: I like it -8 Vote: I do not like it

It is not clear to me why the total complexity for D is O(mn). Could somebody explain it to me?

→ Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can someone give the DP solution for Problem C? Thanks :D

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

http://mirror.codeforces.com/contest/489/submission/19787251

I don't see why my adjacency matrix approach didn't fit in the time limit for problem D, it should takes O(n) for each new path and O(nm) in total for solving the problem, which is the same as the editorial's solution.

Could any help please? Thanks in advance, any suggestions would be appreciated. =D

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

in problem B.

how to apply maximum flow.

→ Reply
»
6 years ago, # |
  Vote: I like it +1 Vote: I do not like it

Can somebody explain BerSU Ball's recursive DP solution?

→ Reply
»
6 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Just in case there is a harder variation of 489A — SwapSort, there is an O(n * log(n)) method (that kinda resembles using a linked list to me): 53566076

→ Reply
»
5 years ago, # |
  Vote: I like it 0 Vote: I do not like it

What is the complexity of D solution? I'm pretty confused it. My opinion is (n^2 +m). Is that right?

→ Reply
»
5 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can problem B be done Online ?

→ Reply
»
5 years ago, # |
  Vote: I like it 0 Vote: I do not like it

My code for C fails on case 4 not sure why... Any help would be much appreciated

→ Reply
»
2 years ago, # |
  Vote: I like it 0 Vote: I do not like it

https://mirror.codeforces.com/contest/489/submission/176150923

This is my solution to the D problem,
Any idea why this fails
I did it in O(nm + n^2) = O(nm)

→ Reply