onlydmc123's blog

How to find prime numbers in some interval?
By onlydmc123, 10 years ago, In English

I know that you can use sieve of Eratosthenes for finding all prime numbers in (1,N) interval, but can you suggest algorithm that can do that for (N,M) interval, when N,M are large, for instance 10^9 and N=500,000,000; M=501,000,000.

  • Vote: I like it
  • +3
  • Vote: I do not like it

Comments Comments (10)
| Write comment?
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

If the difference between N and M is less (about 10^5), then a modified sieve will work.
You need to cancel out all multiples of 2, 3, 5, and so on upto prime just less than or euqal to sqrt(M).

→ Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Are you talking about this problem?

→ Reply
»
10 years ago, # |
← Rev. 3   Vote: I like it 0 Vote: I do not like it

Hi, you could search about segmented sieve, look this problem http://goo.gl/6nlsFP and its respective editorial http://goo.gl/oAjzCT both resources belong to codeforces user lbv, I hope that this has been helpful.

→ Reply
»
10 years ago, # |
← Rev. 3   Vote: I like it 0 Vote: I do not like it

Find all prime numbers between 1 and sqrt(10^9), and for all numbers between m and n look by sieve, all numbers that divisible for this primes(except this primes) is not prime. Аsymptotic will be O(N(log(log(N)))+(n-m)*mehrunesartem(n-m)). If you want, I can write pseudocode.

→ Reply
»
10 years ago, # |
← Rev. 3   Vote: I like it +1 Vote: I do not like it

I solved it in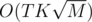 , where K = M - N

If there's no divisor of X, which is not greater than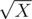 , then, there's no divisor, which is greater than 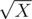, so X is prime.

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Can you explain how you do it?


    T <= 10
K <= 10^5
Sqrt(M)<=sqrt(10^9)

    I think it will be TLE.

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Hmm, then I'm not sure :)

      Actually, I think that was O(TKlogM). Half of all numbers divide by 2, 1/3 divide by 3, etc.

      → Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I know, that in java there is method n.nextProbablePrime(), that find first prime number after n and it's complexity is like O(n^(1/3)), but I don't know, how it works.

→ Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

You can use the Miller-Rabin test, which applies Fermat's Little Theorem to test whether a number is prime. So if we're given n, the number we're testing, we write n - 1 = 2ab, and take some integer k and look at kb, k2b, k4b and so on up to k2ab, all modulo p. If we ever have a residue not equal to  ± 1 that squares to become 1 modulo p, we know n can't be prime. This is because if p were prime and x2 ≡ 1 modulo p, then x ≡  ± 1 modulo p. More details can be found in the second half of this PDF.

If the numbers we are all testing are less than 4.7 billion, it suffices to test k = 2, 7, 61, according to this page. And for each test, we can do exponentiation by squaring to get all the needed powers of k in time. So each primality test can be done time, which should be fast enough for the problem. (They usually call Rabin-Miller a 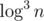time algorithm, but I'm pretty sure that's only after considering implementing bignum multiplication, which we don't have to do because we can just use long long's for everything).

Also, look at this.

→ Reply