Let's restate the problem statement:
- You need to maintain a set of alive soldiers.
- You are asked to perform some queries [L, R]: remove all soldiers with index in range [L, R]. And then find the soldier with maximum index which is still less than L, and the soldier with minimum index which is still greater than R.
The most simple way to implement this is to use C++ set. For each query:
- Find one soldier whose index is in range [L, R].
- Remove that soldier
- Repeat until there is no soldier in range [L, R].
This implementation runs in O(N * logN), because:
- For each soldier, he is only removed once from the set.
- For each query, if we remove k soldiers, we need to do binary search (lower_bound) on the set k+1 times. So the total number of times we binary search is at most N + Q.
Consider the figure in the problem statement. In here we have 4 columns:
- Column 1: 3, -5, -8, 3
- Column 2: 3, 2, 9
- Column 3: -8, -2
- Column 4: 7
Consider a possible configuration of choosing balls.
Let's call the number of balls chosen for at each column xi, where i = 1..N. In the example, we have:
- x1 = 4
- x2 = 3
- x3 = 0
- x4 = 0
It is easy to see that x1 ≥ x2 ≥ ... ≥ xN.
From this observation, we have the following DP:
f(j, k) = maximum value, if we consider the first j columns, and at column j, we choose at least k balls.
f(j, k) = max(f(j - 1, k') + a(j, 1) + a(j, 2) + ... + a(j, k)) for k' ≥ k
You can read this comment. Thanks terribleimposter
100540D - Diccionario Portunol
To solve this problem, you must first know about trie.
First, construct 2 tries. One for prefixes of Portugese words, and the other for suffixes of Spanish words.
For example, in the first example, the prefix trie for Portugese words will contain:
- m, ma, mai, mais
- g, gr, gra, gran, grand, grande
- un, und, undo.
Note that I intentionally removed the prefix "m" of the 3rd word, because it is repeated.
After building 2 tries, you can see that the answer is "near" (size of trie 1) * (size of trie 2). I said near, because there are some words that were counted more than once, for example: "grande" = "g" + "rande" = "gr" + "ande" = "gra" + "nde" = ...
So you need to find how many words are counted more than once. This can also be solved using the tries we just built.
Let denote by + the string concatenation operation, and let a, b, x, y be strings and w be a character.
Consider Portugese words: a + w + x and b + w + y. We can easily see that for each non-empty string a and y, this word is counted at least twice. To count these duplication, we need to count how many pairs of (x, b) exists for each w. For each character w, this value equals to the number of suffix of Portugese words starts with w, times the number of prefix of Spanish words ends with w.
See my code for more details.
100540E - Electrical Pollution
Let's denote by F(x) the anomalies produced by generator at point(x, x).
I have not solved this, but I have the following idea:
- Create a graph. For each equation of the form: F(x) + F(y) = a, add edge between vertex x and y.
- For each connected component of the graph, choose one vertex z, and represents all F(x) = const - F(z). After doing this, for components with cycles, you should be able to get values of all F(x).
- To answer queries, just use the values of F(x) calcualted above.
Since I haven't implemented this idea, I'm not sure if I've missed something.
This problem requires Suffix Array.
First of all, concat all the strings in input, separated by some unique characters (For example, use characters with ASCII code 1 to F).
Build Suffix Array on this string, and calculate LCP array.
Now, to count the number of searchable set, observe the following facts:
- For each searchable set, there's a keyword K for this set.
- This keyword K corresponds to a prefix of a suffix in our Suffix Array.
- It's transparent that the searchable sets have consecutive suffixes in our Suffix Array, where K is their prefixes. Because of this, the corresponding LCP of these will be at least |K|.
So, we can iterate through all searchable set, by iterating through K, but we must do this while keeping the following in mind:
- For each searchable set, there can be more than one K. They can be substring of each other. To avoid duplication, we must store all the searchable sets in a hash table (for example, use C++ set).
- When we iterate, we use Suffix Array. For each position, we consider it as having the smallest value of LCP in our set.
There are some more implementation details, and it is hard to explain everything here. Please refer to code.
This should be a sweep line problem. During contest, I've tried rotating the points, but it did not work (probably because the function we're calculating is not continuous, so rotating can not work well?)
This is a graph theory problem. To solve this problem, you must be familiar with [bridges](http://en.wikipedia.org/wiki/Bridge_(graph_theory) ).
Let's say we need to answer query A B. Find an arbitrary path from A to B. Then, you can see that this path is unique, if and only if all the edges on the path are bridges of the graph. Proving this is a bit tricky, though it is easy to understand why this is correct:
- If one edge on the path is not bridge, you'll be able to construct another path from A to B.
- If all edges on the path are bridges, obviously, you have only one path.
Based on the above observation, you can solve the problem as follows:
- First, remove all edges of the graph which are not bridges.
- Then, use disjoint set (also known as DSU) to maintain the connected components in this new graph.
For each query, you just need to make queries on disjoint set to check if 2 vertices belong to same connected component of the new graph.
This is a straight-forward implementation problem:
- For instruction of type B, just compare the input with each Braille characters to find the corresponding digit.
- For instruction of type S, just print the Braille characters corresponding to each digit in input.
Since the size of input is small, any naive implementation should run in time.
In this problem, you are asked to perform two types of queries:
- Modify one element of array
- Calculate hash value of a subarray.
The most straight-forward way to solve this type of problem, is to use some Data structures that can handle range update & query. I used segment tree. If you are not familiar with it, you can read more here and here or at many other places on the Internet.
In addition to Segment tree, you need to know how to do combine the Hash values of 2 consecutive segments. Let's say you have segment [u, v] and [x, y] where v + 1 = x. If you know hash(u, v) and hash(x, y), you can calculate hash(u, y):
hash(u, y) = hash(u, v) * By - x + 1 + hash(x, y).
You can read my code to see how I implemented this Segment tree.
This is again an implementation. Though, you need to handle corner cases very carefully. One downfall is that each number cannot appear more than 4 times. Let's call the 3 numbers in input a, b, and c.
if a = b = c: Then, if a = 13, there is no solution, otherwise, the optimal solution is set containing three a + 1.
if a, b, c are pairwise distinct: You can use the smallest pair: 1 1 2. This works because no number can appear more than 4 times.
The last case is where a, b and c forms a pair. For this case, I used brute-force to check for every pair. If no pair is greater than this pair, this pair must be 13 13 12, and you can use the set 1 1 1.
See my code for more details.
L & M solution will be updated if I can solve them.











You don't need binary search to solve problem A.
You can solve it in linear time o(N+Q) simply by keeping, for every soldier, the first soldiers to the left and to the right that are still alive. Here is my code: Code
There is also quite straight-forward solution of problem F with suffix automata. Code.
Here is my idea about problem M. But it's not complete.
Firstly, I use a binary string express the init situation, the i-th digit is '1' if there is a pawn, otherwise is '0'.
If the (M-1)-th digit is '1', the problem is quite simply.
How about the situation that the (M-1)-th digit is '0'?
I think if the first one have a winning move, the move before his last move (move a pawn to M-th digit) must make the binary string to 001111(N '1's)...000(all '0'), the leftmost digit is M-th digit.
So, the distance between init situation and 001111(N '1's)...000(all '0') is the key of that problem.
If the '1's are all dis-adjacent, the distance is (M-2) + (M-1) + ... (M-N) — all pawns' digit. But the problem become very complex when some '1's are adjacent.
I noticed that N <= 10^6, so maybe we could get something like SG(X), X means the size of one adjacent '1's' group.
Anyway, If someone solved that problem, please share your idea with me. Thanks.
Just time I have solved it,and this problem take me (long long)time.. This is a model of stone game
for both players,they mustn't move the pawns to position m-1,otherwise he or
she will lose,so the final result is their is a pile of pawns at position
between m-1-n and m-2 (inclusive).
we denote dist[i] as the distance between ith pawn to position m-2 minus the number of pawns which have bigger x[i]. for all pawns which have same dist[i],we can change any number of them to
dist[i]-1,that is to say we can regard them as a pile of stones and change
their parity .so we can choose the pawn of odd dist[i],compute the number of
block of them as their sg number of this pile of pawn,and Xor all the sg
number which have odd dist[i] s.(I think choose even dist[i] has the same
result).
I am not able to solve the problem. can you please look into my submission.
Can you explain this line?
if (i < n-1 && sa.LCP[i+1] >= a[id].length()) continue;In the loop:
I'm counting the number of strings, that is not a substring of any other string. This means that the set containing only this string is good.
For this to be true, for a string S consider the previous suffix P & the next suffix N. Then, LCP(S, P) must be less than |S| and LCP(S, N) must also be less than |S|.
For LCP(S, P) < |S|, I used the condition:
For LCP(S, N) < |S|, I used the condition:
Thanks for quick reply. Does
LCP[i]mean longest common prefix ofi-1andisuffix? If so, what doesLCP[0]mean?it doesn't mean anything.
OK. Thanks, I had doubts, because in my implementation it's opposite
LCP[i]— lcp of ith and i+1th suffix. :)You're using variable
ito separate strings in all. (i < = 60 < = 'a'), so is this line really neccessary?Yes. That line is necessary. The two have different meaning, though it's a bit hard to explain in a few words.. But I'll give a try anyway:
When concat strings, I used different separators. This is to avoid messing up my LCP calculation: when iterating through searchable sets, I extend the set as far as possible to the left and right. Having separators avoid strings to be added unexpectedly.
In this if condition, I'm taking care of the case when the searchable set has only 1 element. For a string S, it fails if there's suffix T of another string, which have S as prefix. When this happens, the two string will be next to each other. Separators doesn't have anything to do here.
If you still don't understand, you can probably write some small cases on paper. It should not be too hard to understand.
Oh, I meant this line:
if (sa.LCP[i] >= a[id].length()) continue;(change from my implementation, again).I thought since we have anyseparator < anyletter, when S is substring of T, it's always before T in suffix array, so we can check only
LCP[i+1].But now I see, that we can have two or more the same words.
You're absolutely right. Thank you for your replies :).
Solution for Candy's Candy:
Let there be 'k' candy's of each flavor in any variety pack, 'n' total flavors, 'f' total variety packs, a[i] total candies of each flavor and p[i] flavor packs of the ith flavor of candy.
Now, a[i] = knp[i] + kf
So, k is a common factor of all a[i]'s. So, k is a factor of gcd(a[1], a[2], .. , a[n]).
Now, for each k, if we find out all possible values of f, then for each possible value of f, we have exactly one possible configuration.
So we should find all possible values of f now.
(a[i] / k) — p[i] * n = f
Since this is true for all i, we get (for all i),
(a[i] / k) % n should be equal and a[i] / k should be greater than n. (Since p[i] >= 1).
Number of values of f for a given i is: (a[i] / k — 1) / n.
(This is obtained by setting p[i] = 1, 2, .. till all conditions remain valid). So, total number of possible values of f is the minimum of this quantity for all i.
Hence, for each factor of gcd, add the minimum to the answer if the condition is satisfied. :)
My Code
My (proposed) solution to E:
Measurement is a sum of X + Y, where X is amount of anomalies from point (X, X) and Y is amount of anomalies from point (Y, Y).
We've got M sums A + B and we need answers for Q queries for sums C + D Let's create graph, where we link vertexes A and B with edge of weight X (measurement: A + B = X)
When can we answer query for C + D?
- if there is a path with odd number of edges between C and D, or:
- C and D are in component with odd cycle.
Why?
We have path from a1 to ak, when we know a1 + a2 = c1, a2 + a3 = c2, ..., ak - 1 + ak = ck - 1. So a1 = c1 - a2 = c1 - (c2 - a3) = ... = c1 - ((((constants - ak)))).
We can derive a1 + ak when amount of brackets is even, otherwise we've got a1 - ak.
Value for this sum will be c1 - c2 + c3 - ... + ck - 1
When there is odd cycle we can get a1 + a1, so a1 as well. If we can get value for one vertex, we can get for all vertexes in component.
How to code it?
It's easy to find odd cycle and values for all component. If there's no odd cycle in component and component is a tree we can use modified LCA to get values for a + b in O(logn).
But what if it's not a tree?
We can use find-union on graph G' with 2 vertexes vo, ve for all vertexes v (odd path, even path). When we link v and w, we link ve and wo and vice versa. If ve and wo are in one components, there is odd path between v and w.
But how can we get value for this path? Is O(n) enough?
"But what if it's not a tree?" Create a DFS tree of the component since we just need any odd length path between two vertices. You can prove that: if between two vertices there is no odd length path in DFS tree, there won't be an odd length path between them in original component also.
Even LCA is not required after that. In DFS tree, out of two paths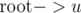 and
and 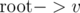 one of the will be included with negative weight, so path
one of the will be included with negative weight, so path 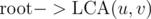 will get cancelled.
will get cancelled.
For problem D, I constructed two tries.
Then I take as much as from Portuguese words and then take suffix from spanish words. At a given node, if char c is a child, I go to it otherwise I add the distinct suffixes starting from c for every lowercase character.
I have considered the corner case where the whole prefix is a valid combination of some prefix and some suffix.
I get correct answer on given test cases but WA on test 2. Any hints about the same?