Abra's blog

Pi calculation
By Abra, 14 years ago, translation, In English
Today's date recalls one interesting task from spoj.pl.
It's easy - just print as many correct Pi decimal digits as possible.
I've tried a lot of methods
from easiest (~200 digits)

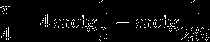
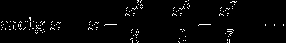
through funny (~1000 digits)
 

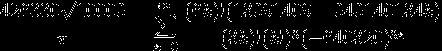
to the most effective I've found (~7300 digits)




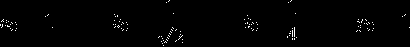
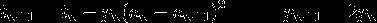
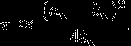
Also I have an idea to use this tricky formula

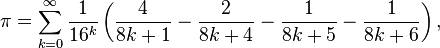
to find hexadecimal digits and convert them to decimal.

My best solution is written in Java and uses BigDecimal and self-written sqrt.

May be I should optimize long arithmetics? Or search for new methods?

Please help me to calculate billion digits =)

  • Vote: I like it
  • +16
  • Vote: I do not like it

14 years ago, # |
← Rev. 3   Vote: I like it +3 Vote: I do not like it
I think this algorithm can be useful.
→ Reply
  • 14 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it
    This algorithm is useful in some way, but, despite very fast increasing number of correct digits, it's slower than the best I tried, 3000 digits against 7000.
    → Reply
14 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

If you want to try a funny method for calculating Pi digits, I suggest you try some fixed point iterations:
x[0] = 3.14 (or anything close to Pi) and then:
x[i+1] = x[i] + sin(x[i]) -- cubic convergence (i.e. x[i+1] has ~3 times more exact digits than x[i]),
or better:
x[i+1] = x[i] + sin(x[i]) + 1/6*sin^3(x[i])  -- order 5 convergence
or perhaps even:
x[i+1] = x[i] + sin(x[i]) + 1/6*sin^3(x[i]) + 3/40*sin^5(x[i])  -- order 7 convergence.

An advantage of these methods is that they are 'fixed point iterations'. As a consequence, you don't actually need to be precisely accurate in your computations, because the iteration will converge to Pi for any decent approximation. So you should gradually (according to convergence order) increase arithmetic accuracy as the iteration proceeds.
Also notice that only one sin() has to be computed at each iteration, the rest is just a polynomial combination.

So the whole difficulty is now in calculating sin(x). Note that using some standard series around x=0 would be very inefficient, because x will be closer to Pi each time. A funny recursive method to calculate sin(x) is

sin(x, depth) = 3t-4t^3, where t=sin(x/3, depth-1)
sin(x, 0) = x

More depth - more accuracy. Also you could replace base condition by e.g.
sin(x,0) = x - 1/6*x^3,
or include even more terms, then you'll be able to use smaller depth. You'll need to find an optimal combination.

→ Reply
  • 14 years ago, # ^ |
    ← Rev. 2   Vote: I like it +5 Vote: I do not like it
    Also, forgot to mention, fixed point iterations natually lean themselves to different convergence acceleration methods. For this concrete case I would suggest Aitken's acceleration method: calculate 3 values of iteration, then using those three values calculate
     Aitken acceleration method
    And start the next iteration from Ax (instead of x[n+2]).
    → Reply