chrome's blog

Topcoder Single Round Match 643
By chrome, 10 years ago, translation, In English

Hi there!

Tomorrow Today at 20:00 MSK will be held Topcoder SRM 643

Let's discuss problems after contest!

  • Vote: I like it
  • +50
  • Vote: I do not like it

»
10 years ago, # |
  Vote: I like it +14 Vote: I do not like it

I deleted my blog, so people do not get confuse. We will do discussion here. Thanks.

→ Reply
»
10 years ago, # |
← Rev. 2   Vote: I like it -8 Vote: I do not like it

Div1 medium greedy? How to solve it?

P.S. Answer after the contest will finish.

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +16 Vote: I do not like it

    I solved with DP. I think most, if not all of the greedy solution will fail.

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
      ← Rev. 2   Vote: I like it +11 Vote: I do not like it

      I believe that greedy might work. But I may be wrong.

      UPD: It passed.

      → Reply
  • »
    »
    10 years ago, # ^ |
    ← Rev. 2   Vote: I like it +2 Vote: I do not like it

    You only need the "vertical or" operations on "HS" or "SH", because either horizontal operation can be replaced by one "vertical or" without changing the result.

    I have a reduction to the "vertical or" operation only: if "HH" is adjacent to "SS", then it's optimal to "or" the "SS" with this "HH", if there's just "HS" or "SH" adjacent to a row of "SS"-s, then we can copy the column with H from either end without changing the answer. That's because each "SS" requires an operation of its own (so the first case is clearly optimal) and a "HS" or "SH" will be converted to "HH" in a "vertical or" operation, which the resulting row of "HS"/"SH" can be made part of. That also gets rid of "SS" columns.

    The best course of action at this point isn't greedy, but DP, because it requires practically no thinking. For example, dp[k][i][j] tells you the smallest number of operations needed to convert states[k][i,j) into all "H"-s. The only interesting operations are "dp[k][i][j]+1->dp[1-k][i][j]" and "dp[k][i][l]+dp[k][l][j]->dp[k][i][j]" ("vertical or" operation and merging 2 substrings). In case you ask why I couldn't solve the problem this way, I'll let this pic say it:

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      what is the "vertical or" operation?

      → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        "H" is 1, "S" is 0 (that's why it's or-ing); it's operation 2, since each pair gets or'd vertically; the other 2 horizontal operations can be viewed as one "horizontal or" where we can pick subseequences instead of substrings, and X->Y means Y =min(Y,X) in this case (transition from state X to state Y, use common sense for what operation needs to be done with their values). Of course, we don't need to turn "H" into "S" at all.

        → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it +3 Vote: I do not like it

      What is the k in your state?

      → Reply
  • »
    »
    10 years ago, # ^ |
    ← Rev. 2   Vote: I like it +19 Vote: I do not like it

    I solved it greedy:

    First eliminate every index where there is S in top and bottom row by expanding adjacent indexes which have a H with the third operator. It doesn't matter from which side you expand the non SS area.

    Then forget every index which have H in top and bottom, and iterate over array and maintain the state HS or SH and count how many times state of HS turns into SH or SH turns into HS while iterating. Now there are count+1 areas. We can use operator 2 in every other of the areas and then use operator 2 into whole array.

    → Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Im sure this div1 round has the record for most hacks

→ Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

What is Div2 1000 ptr solution?

→ Reply
»
10 years ago, # |
  Vote: I like it +19 Vote: I do not like it

Such a hacky round!

→ Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Anyone know how to check the test cases which I got challenged?

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +8 Vote: I do not like it

    You can do after competition is over on Topcoder site by clicking on your last match in profile and clicking on details before that I don't think you could.

    → Reply
»
10 years ago, # |
  Vote: I like it +1 Vote: I do not like it

My first DIV2-1000 passed :D ( but the other 2 failed :D)

→ Reply
»
10 years ago, # |
  Vote: I like it +14 Vote: I do not like it

Some good challenge cases:

  • 250:

885909753408416474 {2, 999999751}

The complete factorization is 2 * 442954987 * 999999751.

Another common mistake was thinking that you needed to check up to 10^5 instead of 10^6 (cube root of 10^18).

  • 500 (by waterfalls in the practice room):

{"SHHHSHHHSHHHS", "HSSSSSSSSSSSH"}

Expected output: 4

Hs on top talk to bottom, fix Ss on bottom with more two moves, bottom talks to top.

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it

    Another common mistake in d1 250 was to iterate up to N^1/2 after dividing N by all given primes, which is slow for cases N = 2*P, P — huge prime.

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it +3 Vote: I do not like it

      Why it is possible to iterate until 10^7 and get all dividers?

      → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
          Vote: I like it +10 Vote: I do not like it

        Actually, it's enough to iterate until 106 = (1018)1 / 3. After you do this, you'll get all divisors except the ones which are greater than N1 / 3. Obviously, there can be at most 2 such divisors and they will be on adjacent positions in the sorted primes list. The last observation implies that one of these two divisors will be given to us as a hint, thus we can easily find the second one in O(1).

        → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
        ← Rev. 2   Vote: I like it 0 Vote: I do not like it

        only 1 prime u need find will exceed 10^6. so u can iterate until 10^6. and then if N still > 1 then N is one more prime.

        → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
        ← Rev. 2   Vote: I like it +7 Vote: I do not like it

        Actually 10^6 is enought for that. The reason is in the fact that there cannot be more than 2 divisors that are greater than 10^6.

        If there is one such divisor — it either will be in the given list, or will be left after all the divisions.

        In case there are two such divisors, they will be next to each other in the list, so exactly one of them will be given to you. The second one will be left after all the divisions.

        P. S. Too late.

        → Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Why should the cube root be considered?

    → Reply
»
10 years ago, # |
  Vote: I like it +1 Vote: I do not like it

What is the approach for Div 1 250 and how do you get to the solution?

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    Primes up to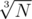 can be found easily and so can the quotient after dividing by them as much as possible. There are at most 2 prime divisors (not necessarily distinct) greater than 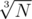and the quotient we got is their product.

    If there are 2 of them, we have to be told one (because they're the largest divisors) and finding the other is trivial.

    Alternatively (and that's how I solved it): we have the time to check primes up to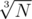 , same for all given primes; if there's anything left, then we can't factorise it in time, so it has to be a prime :D

    → Reply
»
10 years ago, # |
  Vote: I like it +3 Vote: I do not like it

What is wrong with the practise room; "Run System Test" does not work...

→ Reply