The official solution for CodeFest Manthan 2011 Problem E “Save the City!” first computes the range in the edge in question from where each vertex is visible, and then computes the intersection of these ranges. All these ranges can be computed in linear time in total as stated in the solution. Although this algorithm is useful in some contexts, it is overkill for this problem. In this post, I will explain a simpler algorithm.
The algorithm is based on the following fact (Figure 1).
Fact. Let v0,…,vn−1, vn=v0 be the vertices of an n-gon P in the counterclockwise order, and x be a point on the edge v0v1. The whole polygon P is visible from x if and only if for every i=1,…,n−1, the point x is either on the line vivi+1 or on the left of the line vivi+1.
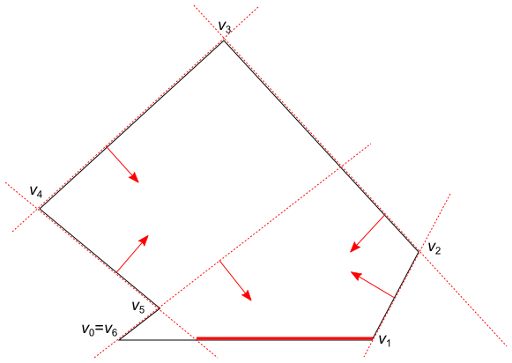
Figure 1
(Here “visible” is defined as in the problem: in words, a point y is said to be visible from a point x when the line segment xy does not intersect the exterior of P.)
Why is this true? Here I give an intuitive argument which hopefully explains the idea. Although it is not a rigorous proof, I hope that it is not difficult to translate it to a rigorous proof once you understand the idea.
Imagine that an ant is at the vertex v1, travels along the edges through the vertices v2, v3, and so on, until it arrives at the vertex vn=v0. You are standing at the point x, always looking in the direction of the ant. If the whole polygon is visible from you, then the ant is always visible from you during this process, and therefore you must have been always turning counterclockwise or staying in the same direction for a while, never turning clockwise (Figure 2). On the other hand, if not the whole polygon is visible from you, the ant must have been hidden behind an edge at some moment, meaning that you must have turned clockwise at some moment (note the red arrow in Figure 3). In short, the whole polygon is visible from you if and only if you never turn clockwise as the ant travels from v1 to vn in this process. By considering when you turn to the left or to the right, we obtain the fact above.
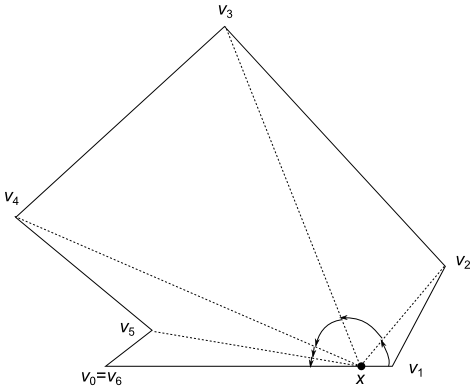
Figure 2
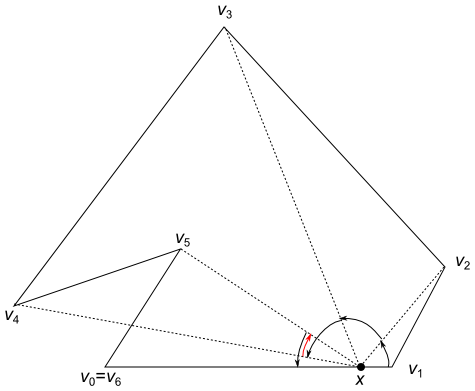
Figure 3
The algorithm is based on the following fact (Figure 1).
Fact. Let v0,…,vn−1, vn=v0 be the vertices of an n-gon P in the counterclockwise order, and x be a point on the edge v0v1. The whole polygon P is visible from x if and only if for every i=1,…,n−1, the point x is either on the line vivi+1 or on the left of the line vivi+1.

Figure 1
(Here “visible” is defined as in the problem: in words, a point y is said to be visible from a point x when the line segment xy does not intersect the exterior of P.)
Why is this true? Here I give an intuitive argument which hopefully explains the idea. Although it is not a rigorous proof, I hope that it is not difficult to translate it to a rigorous proof once you understand the idea.
Imagine that an ant is at the vertex v1, travels along the edges through the vertices v2, v3, and so on, until it arrives at the vertex vn=v0. You are standing at the point x, always looking in the direction of the ant. If the whole polygon is visible from you, then the ant is always visible from you during this process, and therefore you must have been always turning counterclockwise or staying in the same direction for a while, never turning clockwise (Figure 2). On the other hand, if not the whole polygon is visible from you, the ant must have been hidden behind an edge at some moment, meaning that you must have turned clockwise at some moment (note the red arrow in Figure 3). In short, the whole polygon is visible from you if and only if you never turn clockwise as the ant travels from v1 to vn in this process. By considering when you turn to the left or to the right, we obtain the fact above.

Figure 2

Figure 3










