General Comment

I did not spend too much time on thinking about the execution time since the 6-minute is usually much more than the required in the usual online contest (e.g., 2 seconds for CodeForces for instance). So, for each problem, I took whichever way leading me to code reliably.

Also, for each problem, I did lots of stress testing since I screwed up few contests (e.g., the large input in the previous Google Code Jam) before by not fully testing my codes with respect to the full constraint given by the problem. For A and C, I generated the edge cases manually and compared the computed answers from the brute force approaches and made sure they match. For B and D, I generated the theoretical worst case to make sure they are handled properly using my codes.

Thankfully, I hit few segmentation fault problems 4-5 hours into the contest, from which I tried few approaches to increase the stack size; manipulating the size limit in #include<sys/resource.h> did the trick for me. I was so glad that I did the stress testing because if I did not there was no way that I would have spotted this issue before the submission.

As usual, just in case I found a bug in my implementations though, I waited until 5-6 hours before the submission deadline to start submitting the code; I think it is roughly the optimal time frame, since I would like to chew on the problems a bit more yet I would like to avoid a technical mishap where the URL goes down due to a crazy submission rate in the last minute.

Though I thought I did everything right, during this round, I hit an interesting problem in downloading the inputs for B and D, perhaps because I was not using my own computer (a cluster computer was being used); I am so thankful that it was resolved by contacting the contest coordinator through the feedback.

I checked my solutions with my friends', Petr's, and ahmed_aly's; thankfully, I got a match. Then I tested my codes in the Gym; after removing the system calls, I got a few TLE in D because the original limit was set too tight to 15 seconds; I changed calculating in long long to int and used few other tricks to bring down the time to where it is now: roughly 8 seconds.

10: Homework

This problem can be treated by pre-calculating the primacity using the sieve, followed by the usual trick of the cumulative sum, which was my original approach; the cumulative sum approach works since 2 ≤ A ≤ B ≤ 10⁷ and it would be useful when T is large (say T ≤ 10⁷ queries are asked). However, since T is so small, it suffices to calculate the number in a brute-force way, and the latter was probably the intended solution.

By the way, since the product of first 9 primes is already 223092870 > 10⁷, when k > 8, the required answer is 0; this is precisely the idea I used to compute for the pre-calculated table.

Few ways to make the problem harder would be either making 10⁷ as 10¹⁸ (to disable pre-calculating for the table) or making T as large as 10⁸ (basically a constant time per query).

My Submission: 9468217

Modified Submission @CF Gym: 9468787

25: Autocomplete

This problem is a classical question on a trie; I used a fairly standard implementation that I frequently tested in various online judges, adopted from a coding contest bible by JongMan; by the way, it is a great book and you should definitely check that out. I certainly learned and am learning tons from the 2-volume set. I challenge you to find a contest material that is better than that in a book-format.

There is a plenty of room for an optimization especially since the alphabet is limited to only a, ..., z (i.e., only using an array; this is certainly an approach took by some folks), but I used my tested approach to be safe and save some debugging time, especially since the execution time was not too critical.

The system call is disabled in CodeForces Gym. So I had to submit a code without it. It worked out just fine since the default stack size was set sufficiently large.

My Submission: 9468220

Modified Submission @CF Gym: 9468711

25: Winning at Sports

This problem is a standard dynamic programming problem. Given 0 ≤ m < n ≤ 2000, it is sufficient to compute the table explicitly and a lot of contestants did it this way. However, I took the top-down approach, since we may not necessarily hit all the pre-computed values for each valid pairs (n, m) since T is, again, too small.

The key insight is perhaps the following: if we denote the desired quantity using stressfree(n, m) and stressful(n, m) then they both satisfy the recursion of the form f(n, m) = f(n - 1, m) + f(n, m - 1), with some boundary conditions. The base condition is that when either n or m is 0, the required answer is 1 and for the stress-free it is 0 when n ≤ m while for the stressful, precisely the reverse holds, n > m. It turns out we can combine these ideas together and get the answers using just one table, but for the clarity of the implementation, I made a separate function and a table for each.

In my original implementation I cleared out the table each time a pair of inputs is received, but there is no reason to do this. Notice from below that the execution time is improved by a factor of  ≈ 4, but again, the execution time is not what I sought after :)

Of course, one thing to take care of is the mod since the number gets too large for some pair (n, m). This can be approached in a standard way by taking a mod in each summation step.

Although I have not tested, I am sure the same approach would work fine even when the bound is a bit larger (say 20000) or T is larger. I am curious to derive the explicit formula for the two quantities for any pairing (n, m), which can surely be done by, at least, a generating function; I originally thought about the problem using this pathway, but gave up on it since the boundary condition was tricky and the dynamic programming was more than sufficient (and easy enough to code).

Addendum: It turns out the problem is related to the Bertrand's ballot theorem/monotonic path and/or Catalan numbers. Check either the Wikipedia entry here or discussion below for more details. This is the approach I was trying first (using the generating function and etc.) but quickly resorted to the standard way since there was no real reason to think too hard about it unless I already knew the identity; now I do :)

My Submission: 9468238

Modified Submission @CF Gym: 9473189

40: Corporate Gifting

This is yet another standard dynamic programming problem, this time on a graph. The problem statement forces us to a directed acyclic graph; it is directed since it is a managerial relationship and acyclic since two employees are never responsible for each other. Also, since each node has a unique manager and the CEO has no manager, this would force us to a tree with a root at the CEO node.

For each node, we have to save the children in the adjacency list; the matrix is not feasible since N can be as large as 200K. The list would be certainly fine since we are given a tree. Once we have that, to do the DP, only thing we need to take care of is the recurrence relation.

Given that a current node uses a gift x, what is possible for the child? The only restriction is that if gift y is used for the child, y ≠ x. Respecting this, we would like to find the minimum. Of course in the leaf node, we would choose either 1 or 2, depending on whether its parent has already used 1 or not. So, we are led essentially to the following recurrent relation on a node in a tree:

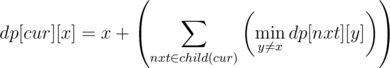
where dp[cur][x] is the minimum attained where the current node is using a gift x. So, at the end, all we need to output is dp[1][0] where 1 denotes the root node and 0 is the sentinel value not used in the computation. The only real issue now is to think about the bound on x, which turned out to be quite trickier than I originally imagined.

I originally thought that the bound has to be 3, but during the stress testing I realized that on some random instances I can get it as large as 5. Then I started comparing the result of 3, 4, 5, 10, 15, 20, and 50. While I compare those results, I tried to come up with the bound on it explicitly. Then, the crude bound I got was log₂(n), which led me to believe that the bound of 20 was enough. I thought about it a little more and in the morning I improved the bound to log₃(n), which led me to believe that the maximum x would be 11 when N = 200000.

Just in case I did not carry out the estimation right, I fixed my bound to 15, from 20; I did not go all the way to 11, since I did not want to cut it too close. I could not find a test case that actually used anything beyond 7 during my random search and thought it was safe enough; I figured I would check whether the answer would change if I used different bound for the provided input and surely enough no change was detected from fixing the bound to 20 or 50, from 15. So I decided to submit the version that used 15 at the end.

After the contest ended, I had a conversation with Ralph, who led me to believe that the right sequence is perhaps the order-consecutive partition, yet to be fully verified; from anyone who can prove this rigorously, I would love to get to know your insight! (See more details here) :)

My Submission: 9468244

Modified Submission @CF Gym: 9468722

Final Remark

To summarize the topics covered in this contest, they were, in short:

1) homework: sieve

2) autocomplete: trie

3) winning at sports: standard dp and Catalan number

4) corporate gifting: dp in DAG and order-consecutive partition

I started entering more online contests and take some online judges (like Timus, SGU, CodeForces Problemset) seriously. Foremost, I would like to thank paladin8 who is patiently coaching me through this entire process. I think it is working out pretty well and I will continuously put some efforts to improve! I now also have a table that keeps track of daily solved problems, coding tricks, and etc.

My current goal is to solve at least 3-5 problems/day from the Timus online judge with a goal of surpassing 500 problems by the mid-year; since I have ~260 problems down, I only have about a half way to go! If there is anyone who would like to join my pursuit to solve the problems in the Timus OJ, please let me know via a private message; I am sure I would get more motivated by a small group going through it together :P

I am hoping this entry would help at least some people out there :)

Any feedback would be much appreciated!!