Thanks to johnathan79717 fo polish my words.
515-A Drazil and Date
If Drazil chooses the shortest path from (0,0) to (a,b), it takes |a| + |b| steps.
So we know that all numbers less than |a| + |b| are impossible to be the number of steps that Drazil took.
Now consider when the number of steps is not less than |a| + |b|.
When Drazil arrives at (a, b), he can take two more steps such as (a, b) -> (a, b + 1) -> (a, b) to remain at the same position.
So we know that for all s such that s ≥ |a| + |b| and (s - (|a| + |b|))%2 = 0, there exists a way for Drazil to get to (a, b) in exactly s steps.
The last part we should prove is that it's impossible for Drazil to arrive at (a,b) in exactly s steps when (s - (|a| + |b|))%2 = 1.
We can color all positions (x, y) where (x + y)%2 = 0 as white and color other points as black.
After each step, the color of the position you're at always changes.
So we know that it's impossible for Drazil to get to (a, b) in odd/even steps if the color of (a, b) is white/black.
Conclusion: If s ≥ |a| + |b| and (s - (|a| + |b|))%2 = 0 print "Yes", Otherwise print "No".
Time Complexity: O(1).
515-B Drazil and His Happy Friends
You may notice that Drazil invites his friends periodically, and the period of invitation patterns is at most n * m (because there are only n * m possible pairs of boys and girls).
So if no one changes from unhappy to happy in consecutive n * m days, there won't be any changes anymore since then.
We can simulate the process of having dinner until there are no status changes in consecutive n * m days.
Because there are only n+m people, it's easy to prove the simulation requires O((n + m) * n * m) days.
But in fact, the simulation takes only O(n * m) days.(More accurately, the bound is (min(n, m) + 1) * (max(n, m) - 1) )
What happens? You can do some experiments by yourself. =) (you can suppose that only one person is happy in the beginning.)
In fact, this problem can be solved in O(n + m).
Let g be the greatest common divisor of n and m. If the i-th person is happy, then all people with number x satisfying 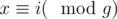 will become happy some day because of this person.
will become happy some day because of this person.
So for each 0 ≤ i ≤ g - 1, we only need to check if there exists at least one person whose number mod g is i and is happy.
If it exists for all i, the answer is 'Yes', otherwise the answer is 'No'.
515-C Drazil and Factorial
Conclusion first:
First, we transform each digit of the original number as follows:
0, 1 -> empty
2 -> 2
3 -> 3
4 -> 322
5 -> 5
6 -> 53
7 -> 7
8 -> 7222
9 -> 7332
Then, sort all digits in decreasing order as a new number, then it will be the answer.
Proof:
We can observe that our answer won't contain digits 4,6,8,9, because we can always transform digits 4,6,8,9 to more digits as in the conclusion, and it makes the number larger.
Then, how can we make sure that the result is the largest after this transformation?
We can prove the following lemma:
For any positive integer x, if it can be written as the form (2!)c2 * (3!)c3 * (5!)c5 * (7!)c7, there will be only one unique way.
Suppose that there exists two ways to write down x in this form, we can assume that the two ways are (2!)a2 * (3!)a3 * (5!)a5 * (7!)a7 and (2!)b2 * (3!)b3 * (5!)b5 * (7!)b7.
We find the largest i such that ai ≠ bi, Then we know there exists at least one prime number whose factor is different in the two ways.
But according to the Fundamental Theorem of Arithmetic, there is only one prime factorization of each integer. So we get a contradiction.
After getting the result, we don't need to worry about other numbers being larger than ours.
Time Complexity: O(n).
515-D Drazil and Tiles
Again we give conclusion first:
First, view each cell as a vertex and connect two adjacent cells by an edge.
Then, build a queue and push all vertices of degree 1 in it.
Finally, in each iteration, we pop a vertex from the queue until the queue is empty. If the vertex is used, go to the next iteration. Otherwise, we put a tile on the vertex and its adjacent vertex, and erase these two vertices from the graph. If it yields a new vertex with degree 1, push it into the queue.
When the queue is empty, if there are still some cells not covered by any tiles, the answer will be "Not unique."
It's easy to understand that if we can put tiles on all cells by the above steps, the result is correct. But how about the remaining cases?
We will prove that when the degrees of all vertices are at least two, the solution is never unique.
Suppose there is at least one solution.
According to this solution, we can color those edges covered by tiles as black and color other edges as white.
We can always find a cycle without any adjacent edges having the same colors. (I'll leave it as an exercise. You should notice that the graph is a bipartite graph first.)
Then we can move the tiles from black edges to white edges.
So if there is at least one solution, there are in fact at least two solutions.
Time Complexity: O(nm)
515-E Drazil and Park
There are many methods for this problem. I'll only explain the one that I used.
Let's split a circle at some point (for example between 1 and n) and draw a picture twice (i. e. 1 2 3 ... n 1 2 3 ... n), thus changing the problem from a circle to a line.
Remember that if two trees Drazil chooses are x and y, the energy he consumes is dx + dx + 1 + ... + dy - 1 + 2 * (hx + hy).
Now rewrite this formula to (d1 + d2 + ... + dy - 1 + 2 * hy) + (2 * hx - (d1 + d2 + ... + dx - 1))
Denote (d1 + d2 + ... + dk - 1 + 2 * hk) as Rk and denote (2 * hk - (d1 + d2 + ... + dk - 1)) as Lk
When a query about range [a, b] comes (The range [a, b] is where Drazil can choose, but not the range where the children are playing), it's equivalent to querying the maximum value of Lu + Rv, where u and v are in [a, b] and u < v.
Another important thing is that Lu + Rv always bigger than Lv + Ru when u < v.
So we can almost solve the problem just by finding the maximum value of Lu and Rv by RMQ separately and sum them up.
However, there is a special case: u = v, but we can handle it by making RMQ find the two maximum values.
Time Complexity: O(n + m).
author's code (implement with  )
)
More information about RMQ: editorial from Topcoder
516-D Drazil and Morning Exercise
We can use dfs twice to get the farthest distance from each node to any leaves (detail omitted here), and denote the longest distance from the i-th node to any leaves as di.
Then we choose a node with minimum value of di as the root. We will find that for any node x, dx isn't greater than dy for any node y in the subtree of node x.
Next, we solve the problem when there's only one query of L. In all valid groups of nodes, where node x is the nearest to the root, obviously we can choose all nodes with di ≤ dx + L into the group. Now we want to enumerate all nodes as the nearest node to the root. We denote the group of nodes generated from node i as Gi.
We can do it in  using dfs only once. (if the length of every edge is 1, we can do it in O(n))
using dfs only once. (if the length of every edge is 1, we can do it in O(n))
Imagine that Gi will almost be as same as the union of all Gj where node j is a child of node i, but some nodes which are too far from node i are kicked out. Each node will be kicked out from the groups we considered at most once in the whole process. Now we want to know when it happens. We solve it as follows: When we do dfs, we reserve a stack to record which nodes we have visited and still need to come back to. Yes, it's just like the implementation of recursive functions. Then we can just use binary search to find the node in the stack that when we go back to it, the current node will be kicked out (the closest node with |dx - di| ≥ L).
So the time complexity of the above algorithm is 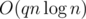
Now we provide another algorithm with O(qnα(n) + nlog(n)) by union find. (Thanks Shik for providing this method.)
First, sort all nodes by di.
Then for each query, consider each node one by one from larger di's to smaller di's.
At the beginning, set each node as a group of its own. We also need to record how many nodes each group contains.
When handling a node x, union all groups of itself and its children. At the same time, for each node j with dj > dx + L, we minus 1 from the record of how many nodes j's group has.
By doing these, we can get the number of nodes j in x's subtree with dj < = dx + L. That's exactly what we want to know in the last algorithm.
author's code (implement with O(qnα(n) + nlog(n))))
516-E Drazil and His Happy Friends
Simplifying this question, suppose that n and m are coprime. If n and m are not coprime and the gcd of n and m is g, then we can divide all people into g groups by the values of their id mod g and find the maximum answer between them. Obviously, If there is at least one group of friends which are all unhappy in the beginning, the answer is -1.
Now we determine the last one becoming happy, for boys and girls separately.
In fact, there's an easy way to explain this problem — finding the shortest path! View all friends as points, and add another point as the source. For all friends, we will view the distance from the source as the time becoming happy. And define two types of edges.
(1)
There is a fact: If a girl x become happy in time t, then the girl (x + n)%m will become happy in time t + n. So we can build a directed edge from point x to (x + n)%m with length n. Similar for boys.
(2)
If the i-th boy/girlfriend is happy originally, we can connect it to the source with an edge of length i. At the same time, we also connect the source to i%n-th boy(i%m for girl) with an edge of length i. You can imagine that the same gender of friends form a cycle. (eg. the (i * m)%n-th boy is connected to the ((i + 1) * m)%n)-th boy for i from 0 to n - 1)
With these two types of edges, we can find that if a friend is unhappy originally, he/she will become happy at the time value which is the length of the shortest path from the source.
The only question is that there are too many points and edges!
We can solve this problem by considering only some "important" points.
- Points connected by the second type of edges.
- Points connected to important points in 1., by the first type of edges.
And we can combine some consecutive edges of the first type to a new edge. The group of edges is the maximal edges that contain deleted points.(These deleted points always form a line).
Finally we find the maximum value of the shortest path from the source to these friends which is unhappy originally in the reduced graph.
Time complexity: 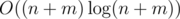










In Div.1 C you wrote
Time Complexity: O(n+m).How to write RMQ that works in O(1)?You can see tutorial from Topcoder.
It's a long long way... (compare to other method of RMQ) I don't implement it.
Apparently here we need to consider two minimum values, so we can't use linear RMQ as a blackbox :P. But it is possible that this algorithm can be modified to handle this also, but I didn't go into the details of this algorithm to check this.
In fact I don't consider the detail as well... But I wouldn't like to think problems now...
[edit] I believe it can change RMQ to find second minimum value now.
It's static RMQ, I believe it can be done with Spurse Table. However, it requires preprocessing of O(n*log(n)), so total complexity is O(n*log(n) + m).
Do you have code for this task with table? I don't know how to find max(Ru+Lv) u!=v
I have just implemeted it, check : 9926495 You just should hold indexes of two max elements in each cell of spurse table, as dreamoon said in the editorial. Let me know if you need any further comments for code
Please fix few mistakes "Unable to parse markup [type=CF_TEX]". Thank you :).
In Div.1 C = Div.2 E, I solved calculating 2 maximum values as follow:
For query range [a,b] 1-A. Calculate max of R_k and index, 1-B. Calculate max of L_k in [a,index-1] U [index+1,b] 2. same as L_k
Div.1 C = Div.2 A — that would be fun ( ͡° ͜ʖ ͡°)
Isn't that vice versa? I've chosen the node with the minimum d_i as root and every node in the subtree had d_j greater than the value of the subtree's root.
First sample seems to be a counter-example for what you-re saying because d_i go there like this:
Here was one big lie ( ͡° ͜ʖ ͡°).
Yeah, missed that. A bit counter intuitive given that in the problem itself we define the opposite distance.
In fact, what I have written was a lie ( ͡° ͜ʖ ͡°). And I think that editorial is not correct that way, but since it's after 5AM, I'm going sleep and not verify that :P.
Now I have fixed it. All thing should be reversed.
Why my solution got TLE on test 19, while I used O(mn) solution?
oh!I think the queue may become too long!so your solution got TLE!
Any proof for drazil and park?
Which part you want to prove?
In division 2 C, how would you find the optimal transformation for large numbers like 9 factorial?
At first notice that we should transformation a digit to as more as possible digits to maximize the answer.
9! = 9 × 8 × 7!. Since 7 is a prime, 7! cannot be divided to more factorials. However, it's easy to see 9 × 8 = (3 × 2) × (3 × 2) × 2 = (3!)2 × (2!), so 9 should be transformed to 7332.
I used n*m days simulation but got wrong answer in test case 41. I got the point of simultaneity of that two event is n*m. What's going wrong?
Try simulating the process using pen/paper for the test case where it failed (41st)
3 20
0
1 19
You'll see that you need more than 60 simulations to make all of them happy.
in div2 b
Because there are only n+m people, it's easy to prove the days in simulation is O((n + m) * n * m). then why solution which are simulating for 1e6 are getting ac as(100+100)*100*100=2e6 I am not able to understand this fact ,anybody please explain it to me
When simulating, we set a counter start from 0. For each day in simulation, We add one to the counter. And If someone become happy, we reset the counter to 0. When counter is more than n*m or all people become happy, we stop simulation.
In the process, counter reset to 0 at most n+m times. So we get the result that our simulation will not exceed (n+m)*n*m.
It is a weak bound for this problem. You can prove the the exact bound is (min(n,m)+1)*(max(n,m)-1) furthermore.
So simulation of 1e6 days is enough.
could you please explain how to prove the exact bound is (min(n,m)+1)*(max(n,m)-1)??
Who can help me? Why this code gets TLE (div 1 — B). Complexity is O(mn) (not O(nmlog(nm))).
9899872
I've inserted
in your solution and got ML25 9911221.
ML? But my vector can't have more than 4*10^6 elements.
Thank you. I got AC. I changed vector to queue then deleted 2 matrixes, which weren't used in my code. 9911687
How to know if there exist a solution in Div.1 B?
By this method in the post, we can only determine whether the answer is unique. We cannot know whether the answer exist or not.
However, you can use bipartite matching to distinguish it in higher complexity.
If someone prints "yes" in place of "Yes", will it get accepted??I am talking about problem A.
You can try it by yourself. Problems of Codeforces with answer contain only yes/no are usually case insensetive.
In Div2. C problem: The minimum number of iterations given as (n*m) is wrong. I got Wrong answer during system test checking( on 41st test case).
Test case is as follows: 3 19 0 1 19
Later I came up with this — The minimum number of iterations required is — [min(n,m)+1]*max(n,m)
Let me know if I'm wrong. I'm getting "Accepted" with this.
I mention something about it at this comment.
Oh okay. Thanks. I skipped that comment of yours.
Hey dreamoon, can you please check whats wrong with my solution to problem 515B? Solution link
I'm not dreamoon, but... First problem is here:
boys[Bindex]== true;girls[Gindex]== true;You use bool operator equels (==), but you should use operator "=" to assign value. However solution is still wrong. Actuallt, B*G iterations isn't enaugh. For example, if one of them is 0
pro100leo Please help me by explaining the reason of Max(n,m)*MAX(n,m) iterations. If Its possible give the link where I can learn those tyof methods. Thanks in Advance.... :) :)
dreamoon_love_AA
I think it's just some math. Not specific method.
Do you read the editorial of Div.1 E? I think you can get some idea after reading it. I like to remain some step to let everyone can think by themselves :P
for div 1 D, can you explain how to solve in O(qnα(n) + nlog(n))
I read your code of Div1 D,but I still don't understand why your method makes the group connected.Could you tell us more detail about it?Thanks.
I add my explain of this algorithm to the post. (I'm sorry for the bad English. Hope you can understand it.)
For any positive integer x, there is an unique way to write x into (2!)^c2 * (3!)^c3 * (5!)^c5 * (7!)^c7.
I didn't got that. How would you write 9 into (2!)^c2 * (3!)^c3 * (5!)^c5 * (7!)^c7 form?
edit: I'm guessing x is a factorial of something!
9! = 7! * 3! * 3! * 2!
Sorry. The sentence should be changed to "For any positive integer x, if it can be written as form (2!)^c2 * (3!)^c3 * (5!)^c5 * (7!)^c7, then it will contain unique way."
Thank for the editorial and rather detailed solutions. And it might be a good idea to ask somebody to edit the english language of the editorial! Let's make it a good practice!
The assumption in Div2-D: if each vertex has at least 2 degrees, the answer is "Not unique" can be proved by dfs from any vertex and go the edge black and white in turn. Because each vertex has at least 2 degrees, finally the dfs will find a circle which has no edges which are adjacent with same color.
Hi, dreamoon_love_AA can you please explain this statement : "Let g to be the great common divisor of n and m. If i-th person is happy, then all people with number x satisfying will become happy some day due to this person." for Div2 B.
I cannot get feel of it.
Because if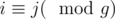 , then there exist some day i-th boy will be invited together with j-th girl.
, then there exist some day i-th boy will be invited together with j-th girl.
can someone please tell why my 2*n + m*(lg 2*n) solution is getting TLE ? Here is my approach , like the editorial , after dividing Lu and Ru , We don't need a segment tree , instead a divide and conquer approach like this ,
let the range we have to calculate be [a,b] we divide the range [a,mid] , [mid+1,b]
Now , the two tree is either entirely on [a,mid] or entirely on [mid+1,b] or first tree is at left and the second one is at right, we solve the first two recursively . and for the third one we find maximum value of Lu in [a,mid] and max Rv in [mid+1,b] and sum them . then we return the maximum of them , why it is getting TLE I can't understand , its obviously lgn. Here is my submission 9938223
Hi,I have found an alternative solution for Div I E using binary search answer, for each number of binary search time T,if for each female group(there are g=gcd(n,m) groups) if there is a value y0 which is not in the list of girl[] (k0*n+boy[0])%m==(k1*n+boy[1])%m==....==y0, for every 0<=i<n+m, k[i]*n+boy[i]>=T,then answer is at least T..
then we can find the interval of solution y0==(k0+boy[0])%m==(k1*n+boy[1])%m==.... (ki*n+boy[i]>=T) if we write as k[i]==k0+dk[i] then dk[i] is solution of dk[i]*n%m=boy[0]-boy[i]. we can solve the interval of every k[i] k[i]>=(T-boy[i]+n-1)/n && k[i]<=m/g-1; if we substitude k[i]==k0+dk[i] then (T-boy[i]+n-1)/n<=k0+dk[i]<=m/g-1.then find the intersection of interval value of k0 for every i.
there may be two type of interval, first type (T-boy[i]+n-1)/n-dk[i]>=0 then there is only one interval:[(T-boy[i]+n-1)/n-dk[i],m/g-dk[i]-1]. second type (T-boy[i]+n-1)/n-dk[i]<0 then the interval is union of two intervals: [(T-boy[i]+n-1)/n-dk[i]+m/g,m-1] union[0,m/g-dk[i]-1].
we can notice the complementary set of second type is only one interval we want to find the intersection of these intervals, first we can find the intersection of inveral of first type. then find its complementary set. then we can find the complementary set of second type. then find union of these intervals. at last find complenmentary set.
if the result interval doesn't contain the value of girl[],then answer>=T.
In Problem (E Div2, C Div1)
dreamoon_love_AA I'm a little confused. Could you provide a proof for this, please!
There are another import thing is Lu + Rv always bigger than Lv + Ru when u < v.So we can almost just find the maximum value of Lu and Rv by RMQ separately and sum them up.I wanna know why we cannot find such
x, y and x > vthatLx + Ry > Lu + Rv?Thanks in advance!
Let's express Lu + Rv and Lv + Ru in di and hi when u < v.
By definition,
Lu + Rv = du + ... + dv - 1 + 2(hu + hv)
Lv + Ru = - du - ... - dv - 1 + 2(hu + hv)
So it's clear that Lu + Rv > Lv + Ru. Which means that, If you get max{Li} and max{Ri} separately you will never get Lv + Ru as max sum where v < u.
Can someone explain what should i do after finding where should each node kicked out of sets with vector? i cant find a way turning that data to each nodes group size data. (Div 1 D)
For problem Div1C is it true that if we find trees i, j such that h[i], h[j] are first and second maximum values and i < j and any tree z, i ≤ z ≤ j is allowed to use , then there is no optimal path which starts or finishes at z such that i < z < j?
Yes, that's true. http://mirror.codeforces.com/contest/516/submission/9951061
In Div1 C Editorial:
"When a query about range [a,b] come, it' equal to query what's the maximum value of L_u + R_v where u and v are in [a,b] and u<v."
Is this mean we choose tree u and v in [a, b]? If so, isn't this contrast with the problem statement (we can't choose tree in [a, b] to climb or stay close to them)?
You are right. The range [a,b] here is not the same meaning as problem.
So in the editorial, [a, b] mean the children doesn't play in this segment?
Yes.
I got that. Thanks!
For problem D Div2, I got this in Java
Verdict: WRONG_ANSWER Input 4 4 ..** ... . .... Output <>** ^<> v <><> Answer <>** ^<> v <><> Checker comment wrong answer 1st lines differ — expected: '<>**', found: '<>**'
could you tell me why I get this error since 1st lines are the same. I use System.out.println(rest[i]); where rest is the array of char-s
sorry for my bad english.
i have a question about problem div 1 — C for first sample test
l is 6 8 0 -4 0 -4 -2 -10 -14 -10
r is 6 12 8 8 16 16 22 18 18 26
we must find max of these intervals for any a and b (a < b) (1, a-1) u (b+1, n) u (n+1, n + a — 1) u (n + b + 1, 2n)
so in first query (a = 1 and b = 3) we must find (1,0) u (4,5) u (5,4) u (9,10) -> (4,5) u (9,10) intervals
4 -> -4 | 8
5 -> 0 | 16
9 -> -14 | 18
10 -> -10 | 26
the maximum value can be (26 + 0), (26 + -4), (18 + 0), (26 + -10)..... we cant use the first value because 26 comes from 5th and 0 comes from 5th. than we use the second value. i found the answer is 22. but why answer isn't it ?
Sorry for my bad English.
In this case, you can only find l,r in interval (4,5). You can think about what Monkey Drazil do if he choose tree 5 and tree 10(i.e. tree 5)
I solved. Thank you dreamoon.
515-D Drazil and Tiles "We always can find a cycle with no edge with same color is adjacent. (Leave as a practice. You should notice the graph is bipartite graph firstly.)"
Should one try to prove the existence of the cycle using ideas from König's theorem proof? I had some difficulty understanding how to make a cycle out of the alternating path mentioned in wiki proof, but maybe I am moving in a totally different direction.
Div 2 B problem is tagged as meet in the middle ... How that solution works ?? Please Explain >>
I don't know why either. @@
Thank you for a very interesting and diverse round :)
At D-problem:
How is it recommended to manage graph here? If we will take each vertex from 2000x2000 matrix we will have 4*10^6 vertices — if each will have adj list (max 4) we will have List for each vertex, i.e. List[4*10^6] should be used in worse case. It's too much! Maybe I missed some? Could you please give a clue how to store it in memory? Many thanks!
I think you can see any AC code to find the solution.
We don't need store all edges in memories. Just refind which edges a point have when we want to know.
Following two submissions differ in only scanning and printing:
10561053 — AC in 170 ms (using scanf/printf)
10560930 — AC in 1122 ms (using cin/cout)
Input size is ~ 4 × 105 ints and output size is 105 long longs. Don't get it.
Alternate $$$O(qn + n\log{n})$$$ solution for div1-D (also, the editorial is pretty bad):
Firstly, its a well known fact that farthest node from any node in a tree is one end of a diameter of the tree. So lets find the diameter of the tree, and compute $$$far[u]$$$ = distance of farthest node from node $$$u$$$ for all $$$u$$$.
Now the tree can be seen in this way: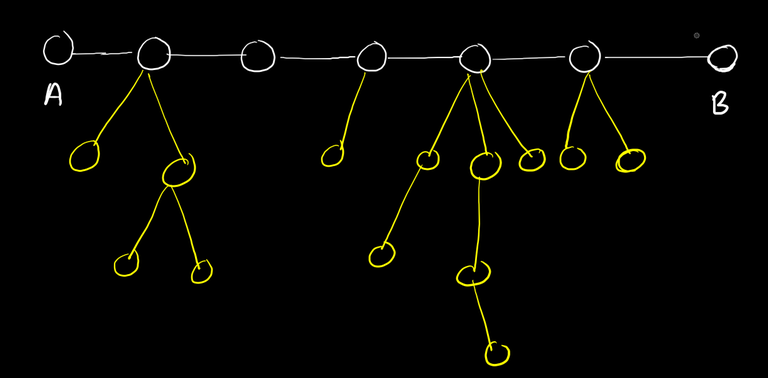 (See the diameter $$$A <-> B$$$, and all the other yellow nodes as parts of trees hanging from white nodes on diameter)
(See the diameter $$$A <-> B$$$, and all the other yellow nodes as parts of trees hanging from white nodes on diameter)
Some observations that we will now use:
Now how do we answer query for value $$$L$$$? Let us try to fix the minimum value of $$$far[u]$$$ amongst all selected nodes in the optimal selection. Call this fixed node $$$R$$$.
Cases:
Now for each query, if we smartly choose order of fixed nodes (in linear manner, iterate away from $$$drop$$$), then we can fix all the nodes in the tree and check the answer for that fixed node, and then take the best one. How to implement this? Its quite simple: link
Now, if we just implement this in a regular manner using a set, it will be $$$O(qn\log{n})$$$. But you can reduce the complexity to $$$O(qn + n\log{n})$$$ by not using a set and instead pre-sorting the nodes by value of $$$far$$$, which is more efficient than the model solution (albeit with high constant factor).