527A - Playing with Paper
It’s easy to see that described process is equivalent to the following loop:
while a > 0 and b > 0:
if a ⩾ b:
a = a - b
else:
b = b - a
ans = ans + 1
But such naive approach will obviously lead to verdict TLE, since it makes ~10, 2015 - 03 - 1912 operations even on the third sample test. The key idea is to replace repeating subtraction operations with integer division operations. This leads to the logarithmic-time solution that looks similar to the Euclid algorithm:
while a > 0 and b > 0:
if a ⩾ b:
ans = ans + a div b
a = a mod b
else:
ans = ans + b div a
b = b mod a
527B - Error Correct System
The first observation is that the new Hamming distance may not be less than the old one minus two, since we change only two characters. So the task is to actually determine, if we can attain decrease by two, one or can’t attain decrease at all.
The decrease by two is possible if there are two positions with the same two letters in two strings but that appear in different order (like “double” <-> “bundle”).
If there are no such positions, then we just need to check that we may decrease the distance. This can be done by just “fixing” the character that stands on the wrong position, like in “permanent” <-> “pergament” (here n stands in wrong pair with m, and there is also unmatched m, so we may fix this position).
Otherwise, the answer is to keep everything as it is. Implementation can be done by keeping for each pair (x, y) of symbols position where such pair appears in S and T and then by carefully checking the conditions above.
528A - Glass Carving
Obviously the largest glass piece at any moment is the one that is product of the largest horizontal segment by the largest vertical segment. One of the possible solutions is to carefully implement what described in the statement and keep all horizontal segments and all vertical segments in priority queue or std::set, or some logarithmic data structure. This solution works in 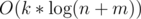 .
.
But there is also a nice linear solution if we answer all queries in reverse order. Suppose segments are not cutting, but merging. In this case we may keep the horizontal and vertical cut lines in double-linked lists and track the current maximum (that can only increase and become equal to the newly-merged segment each time). This solution works in O(k + n + m).
528B - Clique Problem
One may think that this task is about graph theory, but it after some investigation and several equivalent changes in task statement it can be reduced to the well-known greedy problem.
Initially you have that points may lie together in a set if they are not too close, i. e. |xi - xj| ≥ wi + wj. This is obviously equivalent to the following condition. Let’s consider interval of radius wi with center in point xi and call this interval to be the interval of point i. Then the statement actually says that no two such intervals should be intersecting.
This task is well-known and can be solved greedily after sorting segments in ascending order of right endpoint:
Sort segments S in ascending order of S.x + S.w
last = 0
ans = 1
for i = 1..n - 1:
if S[i].x - S[i].w ⩾ S[last].x + S[last].w:
last = i
ans = ans + 1
It’s easy to prove that this solution is correct. Among all ways to choose first k segments, the best way is the one that minimizes x-coordinate of the right endpoint of the last segment (since it restricts us in the least possible way).
528C - Data Center Drama
Problem legend asks you to add minimum number of edges to the given connected undirected graph (possibly, with loops and duplicating edges) and choose direction for its edges so that both the incoming and outgoing degrees of all vertices are even.
First idea is that the resulting graph before we choose the direction (but after we added some edges) will contain Euler circuit, since all degrees are even. That’s almost what we need: if we have an Euler circuit that contains even number of edges, we may direct them like following: a <- b -> c <- d -> e … It’s easy to see that each vertex appearance in this cycle adds 2 to its ingoing or outgoing degree, so the resulting degrees will be even.
But if the Euler circuit is odd (meaning that there is odd number of edges in the graph), we must add some extra edge to the graph before we continue, the easiest way is to add a loop from vertex 0 to itself, since it doesn’t affect the Euler tour, but now tour length is even, so everything is ok.
Now we should think how to add edges optimally. It’s easy to see that the optimal way is to first fix all odd degrees of vertices (i. e. combine all odd vertices by pairs and put an edge in each pair), and then, possibly, add an extra loop as described above. The last part is to actually find an Euler circuit, and to print the answer.
528D - Fuzzy Search
There were issues with this task. Intended constraints were actually n, m, k ≤ 500000, and the intended solution was using Fast Fourier Transformation, that leads to 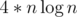 running time. But unfortunately the statement contained wrong constraints, so we reduced input size during the tour. Nevertheless, we will add the harder version of this task and you will be able to submit it shortly.
running time. But unfortunately the statement contained wrong constraints, so we reduced input size during the tour. Nevertheless, we will add the harder version of this task and you will be able to submit it shortly.
Key idea is to reduce this task to a polynomial multiplication. Let’s solve the task in following manner. For each position i of the S for each character c from “ATGC” we will calculate match(c, i) that is equal to the number of c characters that have matching symbol in S if we put string T in position i. Then the criteria for us to have an occurrence at position i is that match(A, i) + match(T, i) + match(G, i) + match(C, i) == |T| (that means exactly that each character from T being put at position i has a corresponding character in S).
Now let’s find out how to calculate match(c, i). Let’s keep only c characters and “not c” characters in both strings and denote them by 1 and 0 respectively. Let’s also spread each 1 in string S by the distance k to the left and to the right. For example, k = 1 for the sample string AGCAATTCAT and the character A corresponding bit vector will be 111110111, and for the character C it will be 0111001110. This bitvector can be calculated in O(n) by putting two events “+1” and “-1” in string S in positions x - k and x + k for each 1 in original string S and then sweeping from left to right over the string S and processing those events.
Now our task is reduced to searching all positions where the bitvector T is the submask of the bitvector S. In constraints n, m, k ≤ 200000 this can be done by using bitsets in O(m(n - m) / 32). Nevertheless, this task can be seen as calculation of polynomials S and reversed(T) product. We will keep this as an exercise for those who decide to submit the harder version of this task.
528E - Triangles 3000
Let’s draw a bounding box that contains all intersection points. Let’s fix a triangle and consider three angles shown on the picture. Calculate area of intersection of those area with the bounding box and call this area to be the “area of an angle”. Then it’s easy to see, that those three angles are complement to the triangle itself in the bounding box, i. e. triangle area is bounding box area minus three angle areas.
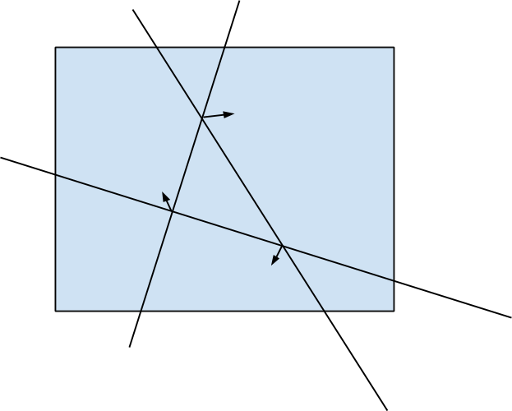
This leads us to the idea how to solve this task by carefully calculating for each possible formed angle on the plane, how much times does it appear in total answer if we sum all values like (S - angle_area(a, b) - angle_area(b, c) - angle_area(c, a)) over all triples (a, b, c) of lines.
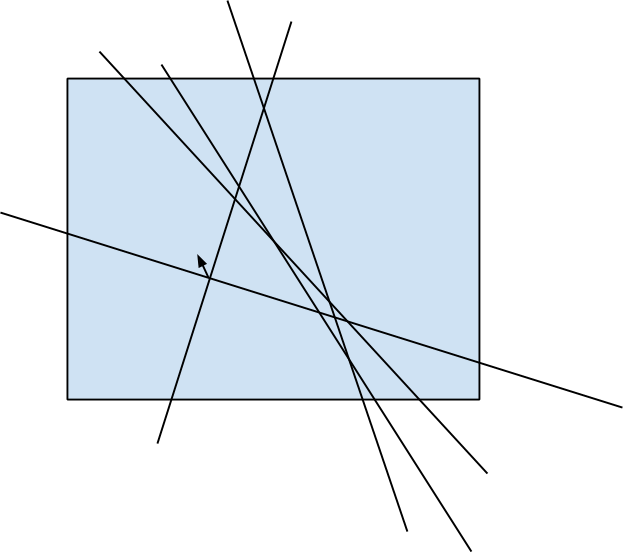
Actually, the angle is considered as many times, as many lines there are that intersect both sides of its right adjacent angle. So, our task is reduced to calculate for each angle on plane how much lines intersect its sides (i. e. its rays).
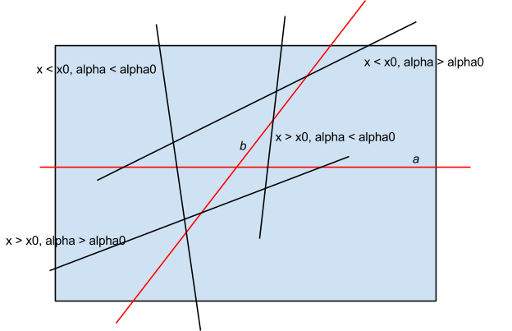
This can be done in  by fixing the first side of the angle and then adding lines in ascending order of polar angle, and then by keeping the number of lines that intersect the base line to the left and that intersect the base line to the right. Key idea is that the exact of four angles formed by the pair of lines (a, b) that is crossed by some third line c, can be determined by two numbers: its polar angle alpha and its crossing with a coordinate x. Further details are shown on the picture below.
by fixing the first side of the angle and then adding lines in ascending order of polar angle, and then by keeping the number of lines that intersect the base line to the left and that intersect the base line to the right. Key idea is that the exact of four angles formed by the pair of lines (a, b) that is crossed by some third line c, can be determined by two numbers: its polar angle alpha and its crossing with a coordinate x. Further details are shown on the picture below.
There is also a nice short O(n2) solution from enot110 here.










There is another short O(n2) solution from piob here.
I think the method of piob has more intuition than method of enot110.
I calculate the answer using the formula for area of triangle given by points A, B, C = [(A x B) + (B x C) + (C x A)] / 2, where x is a vector product (I treat points as vectors from 0). To do that I would iterate over each possible pair of points considering them as a triangle side. For each possibility I calculate the probability it will be indeed a side times vector product for both points. Straightforwardly it will be O(n^3). Instead I calculate the sum for all points on one line in O(n). To do that I use the fact that A x (B+C) = A x B + A x C, where x denotes vector product. There is also a problem with vector product sign. To deal with this one have to iterate over all intersections in the right order (given by angles of crossing lines) and add to the result probability * (current point x sum of previous points). I can sort all lines once, so the complexity is O(n^2).
Thanks for nice editorial, though it was a bit late :)
Can anybody help me with problem D ? I'm getting TLE 23
I am using Z_Function algorithm. We must calculate z-function for string t=T+(some char)+S,
and find all values with z[i]=|T| .(size of T)
if k==0 then in z_function code we must check if chars on positions [i] and [i+z[i]] are same :
but for this problem we want to check if there is char
T[ i ]inS[ i-k ... i , i+1 ... i+k ]so i calculated for all positionsiin S which chars we can get fromS[i-k...i+k]and now z_function code looks like this:
I think that this algorithm is correct, but I don't know why it's getting TLE
I tried to read strings with getchar() but still TLE : 10346382
http://mirror.codeforces.com/contest/528/submission/10346508
You don't calculate z-function for string
t, that is why this solution works in O(nm).And if you actually do it, the solution will be wrong: http://mirror.codeforces.com/contest/528/submission/10346568.
No, then it must be for (i=1, l=0, r=0; i<n; ++i) not i=0 ;) 10346724
And why do you think that it's O(n*m) , I am always increasing r
I think I am using algorithm of e-maxx , which is O(N)
Ok :)
You forgot to calculate z-function for
tagain (arraycanis empty for the firstmcharacters), so solution is still wrong: http://mirror.codeforces.com/contest/528/submission/10346783z-function doesn't work here, because we don't know what is happening outside
[l, r](roughly saying, you need to know about[l - k, r + k]) and you can't just takez[i - l].Ok then i will calculate z-function for T+(some char)+S
and i will calculate z_function for t too http://mirror.codeforces.com/contest/528/submission/10346896
it's still TLE
I changed only n=n+m+1 and can[i+m+1][j]=1; from your code
Oh, you force
z[i]to be less thanm.Example of O(nm) test: http://mirror.codeforces.com/contest/528/submission/10347013
about z[i] < m : http://mirror.codeforces.com/contest/528/submission/10347345
thank you it's TLE on your test too but now i have everything alright :\
One more thing:
z[i]always ≤m, because you addedsome charbetweensandt.I guess, now we understand each other :)
Yes you are right, but now it is normal z-function written by e-maxx,
I only have different function to compare two chars
I tried the same thing and the solution seems work but time complexity changes! Seems some assumptions for time complexity don't work for this comparison function. This is quite interesting fact by itself.
http://pastebin.com/shNC2s5z
This source is for problem div2C. Why I am getting time limit error? I saw that many people solved this problem with that approach too. Could anyone see it?
Thanks !!!
You pass
set<int>to a function by value, so it is copied every time.Thank you !
Can you please help me out of the same situation? This is the solution : http://mirror.codeforces.com/contest/528/submission/12231900
Here you go : 10346629
it takes O( size of set ) time to pass set to function LL find_max()
so your program worked ~ O(N) per query
you can change
auto med=setCut.find(num);toauto med=( (cut == 'h')?(horiz.find(num)):(vert.find(num)) );and it will be AcceptedThank you !!!
For B. Clique Problem i think you should use
|xi - xj| ≥ wi + wjinstead of|xi - xj| ≤ wi + wjin editorial ...deleted
Oh, the sign is indeed wrong. Thanks, fixed.
What algorithm is used to find the Euler Circuit in Div 1 Problem C? I read about Fleury's algorithm but it is O(E^2) where E is the number of edges in the graph and I don't think that will pass the constraints given in the problem. So what algorithm do you use?
You may read about simple O(|E|) implementation here: http://www.algorithmist.com/index.php/Euler_tour
In the cycle finding algorithm, how does the given pseudo code guarantee that the tour we obtained an euler circuit and not an euler path? What I mean is that I don't understand what part of the given code tells us that we have obtained a cycle?
The idea is that if the graph contains only even nodes, then you simply can't obtain an Euler tour that is not a circuit, otherwise the start and end nodes will be odd.
Hmm I can't think of a counter example. Where can I find a proof for this?
The proof is in words "otherwise the start and end nodes will be odd".
Ohh ok because if you can enter then you can leave the vertex as well right? Makes sense. Thanks :)
I have a question, there are a problem when I have this graph, 1-2 , 2-1 , 1-1 , 2-2, If First I go to 1->2->1 I found a cicle, then I remove this cycle, then my graph to convert disconnect(but there are edges rest), in this case What do I need do?
IN 528B — Clique Problem
"ans" should be initialized to 1 rather than 0, to add circle/point with zero index in sorted order.
Yep, you are right.
Hi. Can anybody please explain linear O(k + n + m) solution for 528A — Glass Carving in more detailed way?
Look on queries in reverse order. Suppose you've already done all cuts. Now your task is to remove horizontal/vertical cuts and track the maximum vertical/horizontal segment that exists on the picture.
Let's look on horizontal cuts. At the end we already know all cut positions, i. e. all points. We also know for each point which point is exactly to the left from it and to the right from it, let's keep this information in arrays L[] and R[]. What happens when you remove point x? You need to set R[L[x]]: = R[x] and L[R[x]]: = L[x] to keep the values in arrays L and R correct. This is exactly an implementation of double-linked list. Now the key idea is that if maximum segment could change, then it's new value can be only the (R[x] - L[x]), since this is the only one newly appeared segment.
The same for vertical segments.
Code implementing this solution: http://codepad.org/FAwth2dB
Awesome, thank you
So where is the hard version of D?
You can find it in Wikipedia
I think 528E can be solved by O(n^2) easier
Why in problem C "we may direct them like following: a <- b -> c <- d -> e …"? The graph may be not connected. Am I wrong?
It is connected initially is given in the question. See last line of first paragraph of question.
Thanks a lot
I actually overlooked that the graph in Div1C is connected and solved the problem for the unconnected case. It can be proven that the optimal solution goes like this:
Submission: 10376131
Is there a reason why a simpler version of the problem was given?
What would you do with empty graph on two vetrices? It seems you would add two loops then two edges, but just to edges is enough
There is nothing to do for this graph, we can already "group all the cables coming out of each computer into groups of two" because there are no cables! (I should have specified that we don't do anything for components without edges.)
For those of you who got "Time limit exceeded on test 36" for 528C - Data Center Drama, while finding Euler Cycles, remember to not go through all edges associated with a vertex V every time you visit it.
Otherwise, the time complexity for finding Euler Cycle is:
Instead of
My submissions:
10556106 Got TLE for this one
10556172 AC
For problem A, although my approach is ALMOST same as that given in the editorial, I still get a TLE for the 38th test case. Any help with what's wrong in my code and what can be improved upon/changed, will be highly appreciated.
Here's the link to my submission: http://mirror.codeforces.com/contest/527/submission/15515110
Thanks in advance! :)
Your approach is almost the same as the first provided fragment of code. It is slow and unoptimal since you substract sides one from each other.
Consider a testcase with a = 3, b = 1012. On that test you will perform a subtraction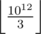 times that won't fit at TL. Idea is that you can combine the consequent subtractions into one operation of taking integer remainder of larger side modulo smaller one.
times that won't fit at TL. Idea is that you can combine the consequent subtractions into one operation of taking integer remainder of larger side modulo smaller one.
Re-read the editorial carefully.
for div2B,
what is the correct output for
4 xoab yxba
?
Err Hi anyone, I wonder how div2D is solved using dynamic programming.
Pardon my noobness :`)
But, in div2 D / div1 B [Clique problem]
One may think that this task is about graph theory, but it after some investigation and several equivalent changes in task statement it can be reduced to the well-known greedy problem
Which well-known problem is this? I'm unable to find it.
Obviously the largest glass piece at any moment is the one that is product of the largest horizontal segment by the largest vertical segment. One of the possible solutions is to carefully implement what described in the statement and keep all horizontal segments and all vertical segments in priority queue or std::set, or some logarithmic data structure. This solution works in O (k * log(n + m)).
But there is also a nice linear solution if we answer all queries in reverse order. Suppose segments are not cutting, but merging. In this case we may keep the horizontal and vertical cut lines in double-linked lists and track the current maximum (that can only increase and become equal to the newly-merged segment each time). This solution works in O(k + n + m).