Recently in a national contest I've found an interesting problem. Given an array of N elements and Q queries with a range 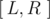 . You've to find how many numbers have the highest frequency in that range? That means if the maximum frequency is
. You've to find how many numbers have the highest frequency in that range? That means if the maximum frequency is 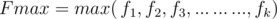 , then how many numbers have
, then how many numbers have 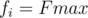 in that range?
in that range?
Let's call the i'th element of the array is 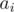 and for each query the range is
and for each query the range is 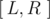 .
.
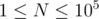
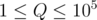
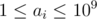

I can't find any feasible solution. I think this problem can be solved using Square Root RMQ with complexity 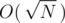 per query. But couldn't find a way. How to solve this type of problem with RMQ? Any idea or hints?
per query. But couldn't find a way. How to solve this type of problem with RMQ? Any idea or hints?
UPD: Mo's algorithm is really cool :D











I believe persistent segment tree is what you are looking for.
I read this. It's about persistent segment tree. But how to implement it in this problem? Can you please explain. Thanks a lot.
realy!
We go from begin array to end and do follow things:
For each a[i] we keep its frequency on prefix. (its easy segment tree, with add in vertex)(we press all numbers).
But we do it like persistent segment tree(we save all state). Then we may get segment on start array, with number's frequency. (It is subtract two tree).
And ans is count max in the tree.
My bad english... I may answer on your question.
I just realize how Mo's algorithm work. I have also a solution which is pretty similar to you but using Mo's algo. Count the frequency for each query in a count array. Before count the frequency of current number, decrease the value of it's previous frequency by 1 (in BIT or Segment Tree). Then after counting it increase the value of new frequency by 1 (in BIT or Segment Tree). And the answer for each query is the max in BIT or Segment Tree.
NB: I think Mo's Technique and Sqrt Decomposition is easy to understand. But I will read about persistent segment tree(I read it at e-maxx but not sure I understand it or not). Thanks for your help.
This problem can be somewhere to try to pass? I have an idea for it, which is based on finding the largest increasing subsequence.
It'll be added to UVA after an online version of that contest. I'll let you know if it'll be added to UVA. Sorry for now.
I guess this problem should not be discussed until the end of this online contest.
By the way, persistent trees in english: http://blog.anudeep2011.com/persistent-segment-trees-explained-with-spoj-problems/
This problem is from an onsite contest which was held a month ago. Problem setter's said that it'll be added after taking an online version of that contest. And I can assure you that there is no restriction about discussing it.
OK. I think it's a trivial modification of the "mode number" problem.
Yes it is. Now I'll read Mo's algorithm. Thanks for your help.
CountZero Can you please tell me that what type of structure we are supposed to maintain in this problem while calculating the number occurring maximum number of times?
I read about MO's algorithm here :- http://blog.anudeep2011.com/mos-algorithm/
In the example that he took he mantained an array which keeps record of frequency of each number
But in this problem what kind of add() and remove() function we have to mantain?
maybe u can maintain tow maps. one for counting frequencies and the other is for counting occurrences of that frequencies. for example if u have an array like this:
1 2 1 1 2 3 3
map1[1] = 3
map1[2] = 2
map1[3] = 2
map2[2] = 2
map2[3] = 1
But that will add an extra factor of logN in the complexity? How to do it in N*sqrt(N)?
The logN factor is for mapping the value because it's quite big. You can use O(1) hash to avoid the logN part.
UPD: But finding max is still logN. I haven't any idea about how to reduce it. Sorry.
then how to find max frequency in O(1)?
ho-jo-bo-ro-lo Finding max is logN. I can't find a better way.
here suf[x] is maintaining how many cnt array index has value >= x
now a variable "ans" that will maintain maximum value in cnt .
now this "ans" will be the maximum frequency and suf[ans] will be the occurrences of such value.
moinul.shaon suppose after performing a few remove() operations suf[ans] becomes zero.
Then how will you get the new maximum occuring frequency?
yes , cnt[x] value may reach negative value (will have to handle RE :p, but i didnt mention here to make it more simple ) , but as you can see the query range will contain atleast one number , so cnt array will never contain zero in all position , after all add and remove operations are performed for a query . so if "ans" variable will be alteast 1 and suf will also be valid .
moinul.shaon thanks for your nice and simple solution for finding max frequency. I think negative problem can be solved by ordering the while loop in Mo's algo. Add first then remove, isn't it?
BTW: Are you a member of BUET_Abacus?
i was wondering about cases like:
1 2 1 2
first query: 1 4
next query : 2 4
for this keeping maximum frequency seemed troublesome but now i realize it's easily possible using the "suf" array you mentioned!
yes , i am @rumman
moinul.shaon
Say we have this example
1 2 1 2
first query: 1 4
next query : 3 4
After first query we'll have cnt[1]=2 cnt[2]=2
also suf[2]=2
So answer will be 2
Now in second query we'll have cnt[1]=1 cnt[2]=1 suf[1]=2
but how we'll update our answer to 1.
Do we need to re-itaerate the whole cnt[] to get the maximum occuring element.
It'd be great if you could provide code for this problem
But by this how
you have to maintain maximum value in cnt in a variable say "ans".
after adding to cnt[x] , if ( cnt[x] > ans )then ans = cnt[x] ;
after removing if ( suf[ans] == 0 ) then ans--;
because in single remove operation maximum value can decrease at most one
moinul.shaon
I have one doubt, Say we have our array as
2 2 2 2 2 3 3 first query is — 1 7 second query — 5 7
say after remove() suf[5]=0
but in your code how will you now update that suf[4]=1
as according to your code value of suf[x] increases only on calling add() function?
Or we have to increment suf[x] also on every remove() operation
i think , you dont even realize what i am doing . suf[x] is maintaining how many cnt array index has value >= x . In first query 1-7 suf will be suf[0]=2; suf[1]=2; suf[2]=2; suf[3]=1; suf[4]=1; suf[5]=1;
"ans" variable will be saving 5 , so occurance is 1.
in second query 5-7, suf[5]will become 0 and "ans" variable will be 4 .again occurence is 1 in suf[4].
i only need to increase suf in add and decrease in remove . the code is correct .
BTW how do you convert it to LIS?
I realized that my idea was wrong. Curently I just know how to find maximum frequency by using LIS.
Yes. But the hardest part is how many distinct numbers are there with this frequency.
A variation of Mo's Algorithm should work I think. :)
http://mirror.codeforces.com/blog/entry/7383
Edit: Beaten by CountZero. ^^
LOL :v. Thanks by the way. :)
I just read the problem and finds a solution that works in exactly O(Nsqrt(N) + Q*(sqrt(N))). Idea is to use Mo's algorithm(offline processing). but before that we can use coordinate compression to map the element in the lower range so that we can use array indexed based hashing and can get faster access time.
Thanks NeverSayNever. After many hours of brainstorming I realized how Mo's algo works. This problem seems hard to solve at first (at least for me). But if any one knows Mo's algorithm then it's a basic implementation of it. Thanks for the help.
I think you have already got the idea otherwise ask for it. I will be more happy in letting you learn this technique.
btw can i get the link to this problem :) .
Sorry bro. Just finished reading Mo's algorithm. I'm looking forward to your technique. But I have some question about Mo's algo. How does it work?
Please elaborate your method.I'm new to MO's algo
Here is a link for you. May be you will have some basic idea. It's new for me too.
UPD: sorry didn't notice that you post this link before me. Never Mind.
This problem isn't added to any online judge. It'll be added soon at UVA. BTW if you have an account or want to register at CodeMarshal you can find this problem at here. The range of an element is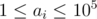 . For your kind information, you can't submit your solution now. You can submit after the online version of the onsite contest which will be held at UVA. Sorry for that.
. For your kind information, you can't submit your solution now. You can submit after the online version of the onsite contest which will be held at UVA. Sorry for that.