Hey you guy's :D
Im wondering, given a number as input, what is the best way to find the smallest palindromic prime number greater than the given number.
Assume the answer fits in long long int as in c++
| # | User | Rating |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 2 | maomao90 | 163 |
| 4 | atcoder_official | 161 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | nor | 153 |
| 9 | Dominater069 | 153 |
Hey you guy's :D
Im wondering, given a number as input, what is the best way to find the smallest palindromic prime number greater than the given number.
Assume the answer fits in long long int as in c++
| Name |
|---|



Palindromes with even number of digits are divisible by 11. Let's start with increasing given N to number of the form abcdcba (palindrome with odd number of digits). Set of prime numbers is pretty dense and here we can expect something similar. I guess iterating over consecutive palindromes is a good idea. So I would suggest loop when first we increase d by one up to 9, then set d : = 0 and increase c by one and so on. After every change we check if this number is prime in O(number of prime numbers up to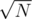 ). In the beginning we must run sieve for numbers up to
). In the beginning we must run sieve for numbers up to 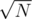 (or up to sth like
(or up to sth like 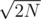 , whatever).
, whatever).
And one more trick. If our current numbers is divisible e.g. by 25 or by 50 then we must change a or b (because we must change one of two last digits) so we shouldn't slowly increase d and c. We must do b + = 1 in this case. So we have special case if our number has divisor which is also a divisor of 10k.