Here is the given information :
Q1 = a; n = 1
Q2 = b; n = 2
Qn = n * ( 1 + Q(n-1))/ (Q(n-2))
// integer division
n <= 10^15
a , b < 10^9
Input : a, b , n ;
Output : Qn
How to solve it ??
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 164 |
| 1 | maomao90 | 164 |
| 3 | Um_nik | 163 |
| 4 | atcoder_official | 160 |
| 5 | -is-this-fft- | 158 |
| 5 | adamant | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 8 | nor | 154 |
| 10 | Dominater069 | 153 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Nov/13/2024 09:49:58 (f1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











Complexity has to be log(n) or better. Try matrix exponentiation somehow.
Obviously recurrence is not linear so it can not be expressed as a matrix.
That is what I am confused about too. But say, if we divide Q(n-2) outside the exponentiation(somehow). Either that, or some formula is there to calculate in O(1). It would be cool if M.E. solution exists, better that finding the formula.
What should you do if Q(n - 2) is zero?
this will never 0..
a = 42, b = 1
Input will be such that No term will be zero ...
There is the similar recurrence in the book Concrete Mathematics at the exercise 1.8
It quickly (in 1-2 elements) converges to 1, 1, 2, 3, 2, 1, 1, 2, 3, 2, 1, 1, ...
assume n >= 3
PS: No proof, just a blind guess...
FIX: 1, 1, 2, 3, 2 corresponds to Qn / n. Of course need to multiply the result by N.
Here are the first 10 terms when a = b = 1:
any pattern???
I try to express the.equation in order of matrix. But how to do that???
The division is not rational, it's integer (truncated). So Qn is divisible by n. But indeed in your case Qn / n converges to 1, 1, 2, 3, 2 after 5th element, not 3rd.
Also I found another counterexamples: for these (a, b) pairs:
(3, 4), (3, 5), (4, 4), (4, 5), (4, 6), (5, 5), (5, 6), (6, 6).
All Qn / n = 2(n ≥ 3). For other 1 ≤ a, b ≤ 100 pattern 1, 1, 2, 3, 2 follows.
Define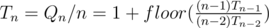 . It is easy to check that for n ≥ 5 (because we can not assume that 2 divides b so n - 2 > 2) if we meet consequent Ti = 1, Ti + 1 = 1 than the following sequence is repeated infinitely: 1, 1, 2, 3, 2. For example for 1, 1 we have:
. It is easy to check that for n ≥ 5 (because we can not assume that 2 divides b so n - 2 > 2) if we meet consequent Ti = 1, Ti + 1 = 1 than the following sequence is repeated infinitely: 1, 1, 2, 3, 2. For example for 1, 1 we have: 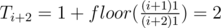 . It is easy to prove these rules:
. It is easy to prove these rules:
It's left to prove that for any a, b we will quickly see any of these patterns. The main idea is that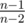 factor does not affect value of Tn if n is large and Tn - 1 and Tn - 2 are small; and for any intermediate values x, y we quickly get to small Tn.
factor does not affect value of Tn if n is large and Tn - 1 and Tn - 2 are small; and for any intermediate values x, y we quickly get to small Tn.
Let's assume we have i ≥ 5, Ti = x, Ti + 1 = y. Then Ti + 2 ≤ 3y, Ti + 3 ≤ 5 (put values in the formula and see).
If Ti + 2 = 1 then Ti + 3 ≤ 2 and so we have matched one of our rules: (1, 1) or (1, 2).
If Ti + 2 > 1 then Ti + 4 ≤ 3 (5/2+1).
So for the algorithm:
FAIL, I solved another problem.