Short Editorial of SRM 658 Div1
Reference Code:
Div2-Easy: http://ideone.com/O7yBlI
Div2-Medium: http://ideone.com/cazTBB
Div2-Hard: http://ideone.com/rxEUcR
Div1-Easy: http://ideone.com/JLuDVM
Div1-Medium: http://ideone.com/7FEz1K
Div1-Hard: http://ideone.com/clL4Rk
Editorial:
Div1-Easy:
The key is that: Any tree is a bipartite graph!
That means, if two nodes are in the same part, then the distance between them is an even number, otherwise it is an odd number.
Assume the 0-th node is in first part, then we can know which part each node belong to by looking at x[0][i] : if x[0][i] is 'E' then i-th node should be in the first part, otherwise it should be in the second part.
There are few things to check:
- x[0][0] should be 'E'.
- there should be at least one node in both part, i.e. there should exist i such that x[0][i] = 'O'.
And then we can check if for all i,j: x[i][j] = (i-th node and j-th node in the same part ? 'E' : 'O'), if not, there is no solution.
Otherwise we can build any spaning tree of this complete bipartite graph, for example we can use this:
1 - 1
1 - 2
1 - .
1 - m
2 - 1
3 - 1
. - 1
n - 1
Div1-Medium:
Suppose for the i-th SCV: it received x9[i] times attack as the first target (so damage is 9), x3[i] times attack as second target, and x1[i] times attack as third target.
If we totally attack t times, then these conditions are necessary:
- For each i, x9[i] * 9 + x3[i] * 3 + x1[i] * 1 ≥ x[i]: this means the i-th SCV must received enough damage to be destroyed.
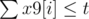 ,
,  and
and 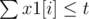 : this means we can't have more then t 'attack as first/second/third target'.
: this means we can't have more then t 'attack as first/second/third target'.- For each i, x9[i] + x3[i] + x1[i] ≤ t: this is because one SCV can not be attacked more than t times totally.
What's amazing is that these 3 conditions are sufficient. I will skill the proof here (In fact I don't have a nice one -- it is ordinary case analysis, if you know a better one then please tell us, thanks!)
Then it becomes easy: First we do the binary search for the answer. Then we can do DP. DP[cur][i][j] := if we use totally i times 'attack as first target' and j times 'attack as second target' to kill all first cur SCV, then what's the minimal number of 'attack as third target' can be?
Div1-Hard:
This task ask the following thing: given a bipartite graph with n nodes in both part, find b: a subset of boys such that: 1. the girl they loves, or say, the neighborhoods of b: |neig(b)| = |b|, that means, any of them don't love girls that is not in this matching. 2. There is a matching of these |b| boys with these |b| girls.
Formula like |neig(b)| = |b| give us a hint for Hall's marriage theorem: Suppose the maximal matching of this bipartite graph is n — d, then we can find b, a subset of boys, such that |b| — |neig(b)| = d. (We can use maxflow algorithm to find such set, by getting the minimal cut)
And then we can do max matching for these |b| boys and |neig(b)| girls, it will give you a valid answer (so we never return {-1}). Why? You can prove the maximal matching of this subgraph is |neig(b)|, once again, by Hall's marriage theorem.











what was the hack on Div2 easy ??
something like {9, 8, 6}
many tried to solve it using greedy that's
(9, 8, 6) -> (0, 5, 5) -> (0, 0, 2) -> (0, 0, 0) => 3
(9, 8, 6) -> (0, 7, 3) -> (0, 0, 0) => 2
he ask div2 easy, not medium
oops, i don't know how but "easy" seemed "500" to me! :P i'm not drunk i swear
[Hint]
Do you know how to solve this problem: Given n string, connect all of them in some order to get a long string, what's the lexicographic smallest one you can get?
Can you solve this problem with this sorting algorithm: If xy < yx then x before y in final order otherwise y before x. When you sort array you easily print s[1]+s[2]...+s [n]
LCM
I took the smallest string and repeted it until it's lenght is not less than the other, but I was hacked :/
Fairly easy solution will be to repeat both strings and make them of length = lcm(length of string s, length of string t). Then simply compare the two resulting strings.
Got my solution accepted this way :)
you mean lcm?
Yes, precisely. Thanks for pointing out, corrected :)
When I see the Fox Ciel and StarCraft, I guess the problems are from you. :)
I can't understand the "<=" in condition 1 of Div1-Median.
"For each i, x9[i] * 9 + x3[i] * 3 + x1[i] * 1 ≤ x[i]: this means the i-th SCV must received enough damage to be destroyed."
Is this right? It would not be >=?
Yes it should be >= ("\geq"), somehow I thought it is 'larger or equal' and typed '\leq'..
Can anyone explain Div-I 500 in a more detailed fashion?
div2 Hard ?
Question about Medium in Div2,if S sum of given vector.Can we find answer according to S?
Wow div2 Easy in 1 line, that is way more efficient that mine, like, 65 lines more efficient.
About Div1-Medium proof, I think what's left is to show, that if you have a matrix with non-negative integers, with sum in each column and each row limited by t, then we can represent it by a sum of t one-zero matrices, each of them having at most one 1 in each column/row. This is the same as proving, that bipartite graph with multiedges can be edge-colored using max-deg colors. And I think, that is a known fact.
anyone from div2 solved div2 easy having the same solution with provided solution in this editorial? i feel bad after seeing the solution :'(, how can i miss that easy approach :'(
In Div-1 medium doesn't condition 3 imply condition 2?
I did a rather brute-force solution for Div1-850 and got accepted (in practice mode).
My solution goes like this. First, start with the full bipartite graph of all relationships, then...
1) Run max-flow.
2) Find all nodes on the left part that are connected to nodes on the right part that still have capacity. Remove those nodes from the left part.
3) If we didn't find any nodes in step 2, print the matching, otherwise, go back to step 1.
I thought it would get TLE, but it actually got accepted.
Can anybody say something about corectness of my code for Div1-650: http://ideone.com/mHcJeB ? I didn't have any reasonable ideas during coding phase, so I went for I-thought-heuristic solution, which may turn out to be correct, but I don't know. I got minor bugs during coding phase, but when I debugged it after contest it got accepted on system test, but I'm still dubious about its corectness.
My idea goes as follows:
We will be using that fact that those 3 conditions are sufficient. Binary search on answer. Then we will proceed with modified greedy. Greedy without modification goes like this "take guy with highest hp and shoot him with strongest remaining shot". It is clearly wrong since some guys with less remaining hp cannot take more than some number of shots and we need to use strong shots on them. So before performing each phase of that greedy (it is divided into three phases of shooting with 9, 3, 1) we will shot all guys with the least number of shots of that value that he has to be shot with. And then proceed with greedy.
If that's correct then its complexity is definitely better than those of model solution, because it runs in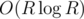 , where R is result, or sth like that, whereas model solution runs in O(R4) or sth (that inner binary search in my code is very stupid, it can be replaced with one formula, but I was too lazy to wirte it down :P). And if it's correct then I think that proof will take advantage of fact that 1 divides 3 and 3 divides 9.
, where R is result, or sth like that, whereas model solution runs in O(R4) or sth (that inner binary search in my code is very stupid, it can be replaced with one formula, but I was too lazy to wirte it down :P). And if it's correct then I think that proof will take advantage of fact that 1 divides 3 and 3 divides 9.
Too lazy to write stress test? :)
{46, 53, 28, 3}Answer is 10, while your solution returns 11.
Thanks :D. I think that sometimes skill of writing good heuristics is also valuable xD.
Can you explain step with maxflow in div1-hard?
You make this kind of graph: for each i: S -> L[i] with cap = 1, R[i] -> T with cap = 1, and add edges like L[i] -> R[j] with cap = INF. Then we could find the minimal cut = maximal match of this graph = n — t.
And the cut contains some of edges like (S->L[i]) and others like (R[i]->T). We collect all boy b such that (S->L[b]) is not removed. Then we know the neighborhood of these boys is all girl g such that (R[i]->T) is removed. And we could verify that |neig(b)| = |b| + t.