Hi!
Recently I've met next problem: set of n lines is given, and they are in general position: no two lines are parallel, no three of them intersect at one point. This set of lines cuts plane into regions, some of which have finite area. Lest calculate an amount of triangles. Let f(n) be a minimal possible number of triangel, and g(n) — is a maximal number of triangles, which can occur.
It is true that f(n) = n - 2 for n ≥ 3. It's been unproven for hundred years, while somebady manage to use tricky matrix method (see article "Triangles and disasters").
Unfortunetely I can't find any inequalities for g(n) in the Internet. One can obtain trivial inequality using Euler formula: let's rewrite a picture as planar graph — where are vertices are line intersections, and edges are segments between vertices(which aren't intersect with some other segments inside). Let amount of vertices be V, amount of edges be E, and amount of faces (parts with finite area) be F. On given picture V = 10, E = 15, F = 6. Actually it's easy to get that g(5) = 5.
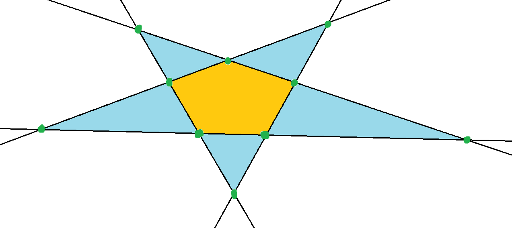
As it's known from Euler formula, V - E + F = 1(we don't count a face which is placed "outside"). It can be calculated easily that V and E equal 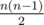 and n(n - 2), respectively, that's why amount of parts with finite area is equal to
and n(n - 2), respectively, that's why amount of parts with finite area is equal to 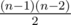 — In fact, that gives a trivial inequality on g(n) as something of order
— In fact, that gives a trivial inequality on g(n) as something of order 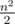 .
.
So, we have a trouble — is this estimation good? Does an example with cn2 triangles exist, or maybe there some better estimation? To show, how this problem is untrivial, I'll show you an example which proves, that g(9) ≥ 14:
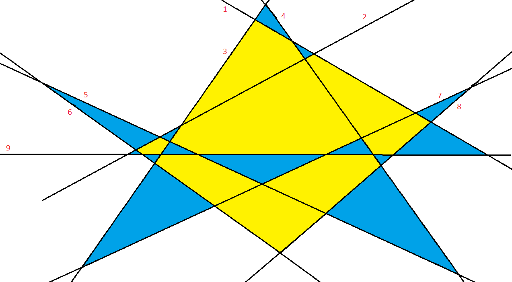
So, a challenge for society: I can prove (with example) that g(n) > c * nlog(n), where c is some predeterminated constant. Can somebody build an example with same amount of triangles? With better amount?:)
update: Examples which prove that 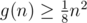 was found by Endagorion and Ripatti, so, the topic is closed:) Example: let's draw a table with n rows and n columns, which almost parallel to each other. Than it's easy to draw 2n - 1 line, which are almost parallel to diagonal of this square, so that i'th line cuts i'th diagonal, so the amount of triangles is quadratic.
was found by Endagorion and Ripatti, so, the topic is closed:) Example: let's draw a table with n rows and n columns, which almost parallel to each other. Than it's easy to draw 2n - 1 line, which are almost parallel to diagonal of this square, so that i'th line cuts i'th diagonal, so the amount of triangles is quadratic.











This thread is very far from being closed.
Proof that is in fact pretty easy and you can find it here: http://artofproblemsolving.com/community/c6h597095p3557339
is in fact pretty easy and you can find it here: http://artofproblemsolving.com/community/c6h597095p3557339
I remember that I had once read article about it in Wikipedia and that it's still an open question to determine exact values of g, but it is possible to give very good estimations. I can't recall exact estimations, but it is possible that differences between some of them were 1. And given bound can't be much better, example with large g(n) can be improved much further than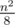
It seems funny, cause I met this problem when I was trying to improve constant c in this problem :)
Some construction like this
gives (n + 1)2 - 3 triangles for 3n lines where n ≥ 2.
Oops, my fault, it gives only constant instead of
constant instead of  I thought earlier...
I thought earlier...
It seems from Swistakk's comment that bound cannot be reached, but your example is nice anyway:)
cannot be reached, but your example is nice anyway:)
By the way, aren't you an author of "Fragmentation algorithm and van der Waerden numbers" on Habrahabr?
I thought I found a counterexample for his proposition. I should check my results more diligently.
Yes, that's me.
I like this algorithm and I even added your article to bibliography in my course work in MIPT. It was concerned with question "what is the minimal N such that if we color numbers 1, 2, ..., N in C colors then exist a nontrivial monochromatic solution of equation x + y + z = 3w", and I used that algorithm to find an answer for 4 colors:)
Glad to see that my article is really useful!
UPD. Seems that this construction won't work.
Nevertheless looks like I know how to improve it a bit.
Consider 3 groups of almost parallel lines on the picture above. We can construct similar structure using them, but it will be very stretched on the plane. Like this:
We will have 3 additional constructions with n / 9 lines. After that we can split (9 groups of lines now) again and build 9 additional structures having n / 27 lines.
So, for n → ∞ we will have (n / 3)2 + 3(n / 9)2 + 9(n / 27)2 + ... + O(n) =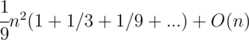 =
= 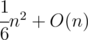 triangles.
triangles.
UPD. Seems that this is wrong too.
Applying the same idea to Endagorion's example, we have
Wolfram Alpha says that .
.
Hey folks, can you check this construction?
Blue lines are bundles of k almost paraller lines, red ones are bundles of 2k ones.
Black dots are Endagorion's constructions, green is mine.
We have n = 12k lines total, for any black dot we have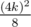 triangles and
triangles and 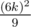 for the green dot. So, total number of triangles is
for the green dot. So, total number of triangles is
Here is described a construction with n2 / 3 + O(n) triangles.
Construction is a bit similar to set of Simson lines. Cool.
Seems that lines not in general position are allowed there.
For tniangles they are in the general position (aka simple arrangement as is stated in the paper).