Hi guys! I'm struggling with a problem and I hope you can help me. You have a matrix of n x m elements between 1 and 10 000( n <= 100 , m <= 100 ). You have to find the maximum area of a submatrix with at most k distinct elements. What's the best complexity you can get? O(n^3) ?
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3985 |
| 2 | jiangly | 3814 |
| 3 | jqdai0815 | 3682 |
| 4 | Benq | 3529 |
| 5 | orzdevinwang | 3526 |
| 6 | ksun48 | 3517 |
| 7 | Radewoosh | 3410 |
| 8 | hos.lyric | 3399 |
| 9 | ecnerwala | 3392 |
| 9 | Um_nik | 3392 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 169 |
| 2 | maomao90 | 162 |
| 2 | Um_nik | 162 |
| 4 | atcoder_official | 161 |
| 5 | djm03178 | 158 |
| 6 | -is-this-fft- | 157 |
| 7 | adamant | 155 |
| 8 | awoo | 154 |
| 8 | Dominater069 | 154 |
| 10 | luogu_official | 150 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Dec/22/2024 23:59:05 (j1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











im not sure of this solution but YOLO
(O(n^2mlg^2mlgn)
we can use 2D fenwick tree that puts "ones" in the place of the last occurence of any number. then for any matrix which has dimensions r * c we can find if it has at most k distinct elements or not. r can be between 1 and n and then we can apply binary search on c to find the maximum area of the submatrix. it will be nlgm tries, you can check if it has at most k distinct elements with 2D fenwick tree by putting "ones" at the last occurence of any number. which is of O(nmlgmlgn) so it will be of O(n^2 m lg^2m lgn)
Your solution seems to be interesting, but I am having hard time to understand it because of complete lack of punctuation. :P
Lol sorry I'll make it better
The first thing that comes to my mind: Fix rowi and rowj, and check for possible coli and colj using 2-pointers. Also keep an array cnt[] of size 10000, where cnt[x] is number of x's in the current rectangle (which is determined by rowi, rowj, coli, colj). This gives a not so appealing complexity of O(R2 * C2 * 1) = O(108).
I need o(n^3) :p
An O(n2·m2) solution:
Let's fix the highest and the lowest row. For each column (within current range of rows) compute prev[col] -- the last column (< col) contains at least one same number and then use two pointers.
One can improve it to O(n2·m):
Fix the highest row and iterate over the lowest in decreasing order. Now we are able to update prev[] in O(m).
UPD: sorry, I misread the problem, I'm gonna try to figure out what to do with k
So, fix the highest row and iterate over the lowest in decreasing order.
For each l maintain persistent dynamic segment tree of size 10^4 which stores amount of each number in [l, r] there r is the rightmost good column. One can get amount of distinct numbers as amount of zeros (= amount of the minimum, since 0 ≤ T[i]).
How to update them when we add new row to the bottom in :
:
for l < n - 1: take T[l + 1], add a[row][l] and keep removing a[row][r(l)] until we would have ≤ k distinct numbers.
UPD: sorry, this solution is actually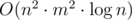
We need to remove a part of a column not just a[row][r(l)], or did I miss something?
Yes, you are right and my solution was wrong.
Can you get it in o(n^3) ?
Is there any Online Judge with this problem?
Tell me your solution if you know please.
Is "submatrix" rectangular or can be sparse too? If rectangular, can it be separated by borders of matrix (e.g. columns 1, 5 in Nx5 matrix)?
Yes, it is rectangular and can be.