SaraGuru's blog

Need Help in a proof
By SaraGuru, 9 years ago, In English

hi friends!! i recently tired to solve the following problem: http://mirror.codeforces.com/problemset/problem/346/A ...i couldn't solve it and in the editorial it was given that the final set always converges to {d,2d,...,max(xi)} where d=gcd(xi)...can anyone prove this statement!! thanks in advance

  • Vote: I like it
  • 0
  • Vote: I do not like it

»
9 years ago, # |
  Vote: I like it +1 Vote: I do not like it

If d divides x and y, then it divides their x - y, so you cannot construct any other numbers. If x and y can be constructed, then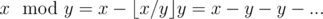 can be constructed. It follows that gcd(x, y) can be constructed because it is calculated by Euclidean algorithm (which is just a series of modular divisions). So d can be constructed too. And finally, if max(xi) = nd, then any number from the set kd = max(xi) - (n - k)d = max(xi) - d - d - ... can be constructed.

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    thank you soooo much!! i have one more question to ask you bro.. during contest time will be able to find such things mathematically or you just go by intuition????

    → Reply