patience's blog

Matrix exponentiation
By patience, history, 9 years ago, In English

Given a Matrix n*n size Let the matrix is A .. Now i have to find out.. A+A^1+A^2+A^3+.......+A^k(k=10^9).. i only can find out the A^k using matrix exponentiation... how can i find the solution of the above equation..

EXAMPLE:
n=3,k= 2
  1 4 6
A=6 5 2
  1 2 3
output:
208
484
722

problem link:http://lightoj.com/volume_showproblem.php?problem=1142

  • Vote: I like it
  • +2
  • Vote: I do not like it

»
9 years ago, # |
  Vote: I like it +11 Vote: I do not like it

This was discussed many times already: A + A2 + A3 + ... + A2n = (I + AN)(A + A2 + A3 + ... + AN)

When n is odd you just find An and get again to the case when n is even.

→ Reply
  • »
    »
    9 years ago, # ^ |
    ← Rev. 4   Vote: I like it +1 Vote: I do not like it

    You need to calc A^n each time. You may use formulas that doesn't require it

    (I + A)(I + A2 + (A2)2 + (A2)3 + ... + (A2)n) for odd.
    I + A(I + A + A2 + A3 + ... + An - 1) for even

    → Reply
»
9 years ago, # |
← Rev. 2   Vote: I like it +22 Vote: I do not like it

Here is another way to calculate that power-sum. Build a new 2n × 2n matrix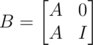 . Taking B to the kth power gives 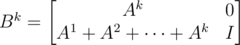. This is easy to prove by induction.

→ Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

To solve the problem, I use classical matrix exponentiation to the following recurrences:

f(0)=A, f(n)=A*f(n-1)

g(0)=O, g(n)=g(n-1)+f(n-1)

This is my code, maybe this help you.

→ Reply