Hi!

Last few days were very tough for me , so I decided to contribute my knowledge which may help someone. Also this will make me feel better.

These are some Concepts which everyone should know and are widely used in Graph Theory.

Chromatic Number: Minimum number of colors required to color Graph G such that no two adjacent vertex gets same color.

Brooks' Therorem: For any connected undirected graph G with maximum degree Δ, the chromatic number of G is at most Δ unless G is a complete graph or an odd cycle, in which case the chromatic number is Δ + 1.

Independent Vertex Set: Set of vertices in a graph G ,no two of which are adjacent that means no two vertices in this set is connected by an edge. (no two of which are adjacent).

α(G) Vertex Independence Number is the cardinality of Largest Independence set.

Vertex Cover: Set of Vertices in a Graph G, such that each Edge in G incident on atleast one Vertex in the Set.

Vertex Covering Number is the cardinality of minimum vertex cover.

• A set of vertices is a vertex cover if and only if its complement is an independent set.

• The number of vertices of Graph G is equal to sum of minimum vertex covering number and maximum vertex independence number.

Edge Cover: Set of Edges in a Graph G, such that every vertex of G is incident on atleast one of the edges in the set.

ρ(G) Edge Covering number is the cardinality of minimum edge cover.

Dominating Set: Set of Vertices ,such that every vertex not in Set is adjacent to at least one member of Set OR Every vertex of G is adjacent to some Vertex of the Set.

γ(G) Dominance number is the number of Vertices in the smallest Dominating Set.

• Independent Set is Maximal Independent iff it is a Dominating Set.

OR

• Independent Set is Dominating Set iff it is Maximal Independent.

Thus,

• Any maximal independent set in a graph is necessarily also a minimal dominating set.

• Dominance Number is always less than or equal to Independence Number.

Matching: Set of edges of G ,such that no two of which are adjacent (pairwise non-adjacent edges) or no two edges share a common vertex.

ν(G) Matching number (edge independence number) is the size of maximum matching.

Matching -> non-adjacent edges

Vertex independent set -> non-adjacent vertex.

• In any graph without isolated vertices, the sum of the matching number and the edge covering number equals the number of vertices.

ν(G) + ρ(G) = n

If Graph G = (V, E) is Bipartite then ,

1. Vertex Independence number is equal to Edge covering number.

2. Matching number is equal to vertex covering number. (König's theorem)

Clique :

A clique of a graph G is a complete subgraph of G, and the clique of largest possible size is referred to as a maximum clique.

ω(G) Clique Number is the number of vertices in maximum clique in G.

• χ(G) ≥ ω(G) Chromatic Number of G is always greater than or equal to Clique number.

A Maximal Independent vertex set of a graph G is equivalent to a Maximal Clique on the graph complement .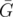

Some Problems :

http://www.codechef.com/problems/SEAGRP

http://www.codechef.com/problems/KMHAMHA

http://www.codechef.com/problems/MACGUN

http://www.codechef.com/CDCRFT14/problems/COPRIME

http://mirror.codeforces.com/problemset/problem/143/D Graph Theory Solution

http://www.codechef.com/DBYZ2013/problems/IITI11

More Problems

I Request everyone to share more Problems which involve these Concepts. Also If there is some Buggy Statement ,Please let me know.

IMP: I will keep updating this blog with new Concepts and Problems , Stay Tuned. : )

Thanks!