Recently i found a problem about geometric, that ask for how many pair of points of the set of points, are good pair, and a good pair is a pair (a,b) of points where the max distance between both points to any other c point it is greater or equals at the distance between the firsts two points ( a and b).
as a formula: distance(a,b)<=max(distance(a,c),distance(b,c))
Can be at most 2000 points.
Is ease see, that can be solve for some O(n^2) whit some factor logn for search a point that invalidate a pair of points, but right now i don't see how search this point. If some one can help me, thank in advance???
UPD: here is the problem: link
Auto comment: topic has been updated by WIL (previous revision, new revision, compare).
For each point, make an array of all the distances to other points and sort it. Then for eachieving pair of points make sure that their distance is the first element in the distance arrays for both a and b.
what if the pair of point are like the image:
both have a lot of near points and are a good pair of points.
Oops, my bad — I totally misread that max as a min. Here's a different algorithm.
For each point, maintain a bitmask of n bits. For all i, initially turn on the ith bit of the bitmask for the ith point. Process the pairs of points in decreasing order of distance. When you get to a pair of points (i, j), compute the bitwise or of the bitmasks for the ith and jth points. If this bitmask has all n bits turned on, then this pair is a good pair. Turn on the ith bit in the jth mask and the jth bit in the ith mask. Note: Some care must be taken to correctly handle when multiple pairs have the same distance, but this is a small implementation detail.
Each bitmask can be represented by n/64 longs (64-bit integers), so each bitwise or requires n/64 operations.
Runtime is (n^2)/2 pairs * n/64 operations = 62.5 million operations.
Not exactly the n^2 * log(n) algorithm you were looking for, but this should be fast enough.
Are (a, b) and (b, a) different pair of points ?
There are the same pair!
I think the main idea is search for points inside the red area
But still do not know how to do it by a faster way.
where can i find the problem??
Auto comment: topic has been updated by WIL (previous revision, new revision, compare).
this probably is not very useful, but you can try to count bad points, fix a point c and count for which pairs c is "bad", this c is the same that appears in your formula.. the question is how to do it in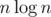
time for a fixed c, for averall complexity 
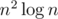. i will try to think about it and if found something i will tell you...
thank, I do the same if i find any solution!
It is of course possible that there is no solution faster than the one mkirsche described. I've spent too much time trying to find a better one with no success.
After some time, i could solve this problem with data structure kdtree, I hope this can help someone.