3-4 апреля в Самарском государственном университете прошел V (XVI) открытый командный студенческий чемпионат Поволжья по спортивному программированию.  Теперь мы приглашаем всех желающих, кто не был на чемпионате, принять участие в соответствующей тренировке 21 июня с 11:00 до 16:00 по московскому времени. Мы полагаем, что участники любого уровня смогут найти интересные для себя задачи, однако наибольший интерес тренировка будет представлять для участников фиолетового и оранжевого уровня (сложность ****).
Теперь мы приглашаем всех желающих, кто не был на чемпионате, принять участие в соответствующей тренировке 21 июня с 11:00 до 16:00 по московскому времени. Мы полагаем, что участники любого уровня смогут найти интересные для себя задачи, однако наибольший интерес тренировка будет представлять для участников фиолетового и оранжевого уровня (сложность ****).
Тренировка пройдет по правилам ACM, задачи будут на русском и на английском языках.
Также просим не использовать интернет, prewritten код и иные материалы — участникам чемпионата это было недоступно.
Контест готовили: Дмитрий Матов (Nerevar), Константин Дроздов (I_love_natalia), Андрей Антипов (Sinner), Андрей Гайдель (Shlakoblock), Елена Рогачева (elena), Александр Ефимов; большую помощь в переводе на английский оказал Игорь Барышников (master_j).
Кроме основного тура были проведены игровой тур и пробный тур, плавно перешедший в April Challenge 1.5, автором которого является Сергей Штейнер (steiner). Задачи April Challenge доступны на сайте соревнований на русском языке, их можно сдать в режиме дорешивания.











А нужно ли заранее регистрироваться на участие в тренировке?
Если я правильно помню, регистрация на тренировку (имеющую фиксированное время начала) автоматически открывается за 6 часов до старта; регистрироваться и участвовать можно до окончания тренировки.
Isn't it a gym contest?
It's a gym contest.
P.S. На сей раз без барж:)
Ну может хотя бы со стремянками?
Неа, приходи со своими, баррэ тоже можешь прихватить:-)
План выполнен, одна из команд пришла с неверным решением жюри и удаленным тестом :)
Where can we find the link to the contest?
Contest will be available in Gym.
Great!!!! and thank's! :D
The registration is open now at gym :)
Как решать G?
dp[i][j] — можно ли через i ходов иметь число j. Дальше ищем достижимое состояние с максимальным i
у меня была динамика. DP[i][j]= 0 или 1 , в зависимости от того можно ли за первые I чисел получить сумму J.
спасибо.
как решать K, I?
I — переберем умение, которое будет минимальным, дальше по каждому ищем минимальное значение, большее данного. Быстро делаем так: отсортируем возможные умения одного типа и будем поддерживать для других указатель на минимальное значение, большее данного.При переходе двигаем как в 2 указателях
I. Перебираем минимальное число которое мы возьмем, и для каждого массива будем брать наименьшее число, которое больше либо равна нашего минимума. Это можно сделать с помощью сета.
К — динамика dp[i][j]: за сколько ходов мы можем поставить на первые i + j мест i букв A и j букв N. С учетом того, что относительный порядок этих букв в оптимальном решении не меняется, можно узнать, какую именно из букв A или N требуется поставить на позицию i + j и посчитать, сколько ходов понадобится на то, чтобы поставить эту букву на место. С учетом dp[i - 1][j] или dp[i][j - 1] в зависимости от взятой буквы считаем dp[i][j].
I — Отсортируем все вместе умения вместе, для каждого вместе с ним храним сферу деятельности. Теперь для каждого i нужно посчитать минимальное j, так что между i и j есть все сферы деятельности. Сортировка за O(nmlog(nm)), остальное за O(nm)
В задаче K можно было перебрать позицию до которой не будет буквы F, и после которой не будет буквы A.
В нашей команде задачу K решил kaliostro за линию: пройдемся двумя указателями — с начала строки для F и с конца строки для A. Для каждой встреченной пары i < j: s[i] == F, s[j] == A — прибавляем к ответу разницу в их индексах (именно столько действий потребуется для обмена этой пары букв) и переходим к следующим позициям.
Вот код решения:
How to solve problem A? I saw a lot of AC on this, but I completely have no good idea on this one.
Minimum spanning tree, answer is maximum edge weight
Thanks you so much!
Let's build graph, where string are verticles abd between each pair of verticles there is an edge of weight equal to difference between strings. Now question is: what is the smallest K such a graph with edges with weights <=K is connected. It can be done using binary search. If we fix K we just do dfs which is going by edges <= K and check if graph is connected
my solution : build graph with recipes. g[i][j] is equal to distance between recipe i and recipe j. then use binsearh for answer: for the fixed answer there shuold be a path with all recipes and without edges with weight greater then anwer
How to solve K? I could not find any approach for this question but it has a lot of AC's so I am guessing it cannot be extremely hard.
After adding posA — posF which of the 2 things is considered processed?
Or do we consider both possibilities by dp somehow?
Letters 'A' and 'F', on positions posA and posF are considered processed at each step
I am sorry to keep on bothering you but could you please explain how your method works?
Just take a pen, write some examples and see that it really works. I don't have any other proofs.
Here's my idea: all we want to do is all As should come before F. Now considering A and F are some values such that A<F now we want to calculate no of inversions ( problem becomes similar to sorting an array with only operation of swapping two adjacent elements. I dont know proof but its equal to no of inversions in the array). Now main problem is every N can be taken as A or F. Which we can solve using a recursive function with two arguments 1.position we are referring to 2.no of Ns considered as F before this position. For every F just count no of As after that position. For every A dont do anything. Now for every N if we consider it as F do same thing as normal F and if its A then add to the answer total no of Fs before this position (original no of F + considered ones). I hope this helps.
Ah yes. This helps a lot.
I was already aware of the minimum swaps = inversion idea and during the contest was trying to reduce this problem into that one but was unsuccessful in doing so (because of the N's). Your solution takes care of that in a very nice manner.
Thank you.
Proof —
If we swap any two adjacent numbers, the number of inversions decrease by at most 1. So, we need at least inversions-count adjacent swaps to sort the array.
And as long as the array is not sorted, we can find two adjacent indices whose swapping will decrease the inversions. So, minimum number of swaps needed is indeed the number of inversions.
On a related note , what if the adjacent condition is lifted i.e. we can swap any two numbers, what is the minimum number of swaps needed ? If all the elements are distinct, we can solve by counting permutation cycles or by a greedy method. If there are equal numbers as well, i am not aware of solution. Does anyone know ?
I used brute force and greedy for this problem I fixed a position 'pos' and solve the minimun number of swaps when all 'A's are on the left of pos, even they can take pos, and every 'F' has to be on the right side.
That's when the greedy steps come....
Closest F to 'pos' on the left side will swap until it stays at 'pos', similar with closest 'A' to 'pos + 1' on the right side will swap until it stays at 'pos + 1', then swap what you have in pos and pos + 1. Do the same until you can't get one 'A' on the right side and one 'F' on the left side.
When there is no 'F' on the left side of pos or there is no 'A' on the right side of pos you'll have to swap 'A' or 'F' with 'N's to achieve the goal.
code : link My solution is O(n^3). I've simulated every step :/, it could be better maybe, without simulation...
nice and greediless :D
Как решать задачи E,H?
Вот мой код для задачи E: http://pastebin.com/48L57tZs
Запускаем dfs от первой вершины.
У каждой вершины есть предки и потомки в дереве обхода в глубину. Пусть мы находимся в вершине V.
Тогда при её удалении образуются несколько компонент связности, среди которых та, в которую входят предки данной вершины.
Для вершины V самый ранний предок до которого можно добраться, не проходя через других предков, выбирается среди тех, до которых можно добраться непосредственно от V и от всех непосредственных потомков. Также для каждой вершины считаем количество потомков.
Пусть мы просматриваем непосредственного потомка U вершины V. Если от U можно добраться до более раннего предка не через V, то при удалении V U будет принадлежать компоненте c предками. Иначе при удалении V образуется компонента, состоящая из вершины U и всех ее потомков.
Итак, для каждой вершины V будут известны размеры компонент, образующихся при удалении V, размер компоненты с предками равен n — 1 — сумма_размеров_остальных_компонент. Ответом является вершина, для которой максимальный из размеров образующихся компонент минимален.
P.S. Кажется, я изобретал велосипед. Если от U нельзя добраться до V или более раннего предка, не используя ребро, соединяющее V и U, то это ребро является мостом.
P.P.S. Код чуть попроще.
Can anyone explain how to solve G or provide a test case for which my submission 11697424 will fail?
Something similar to:
7 5
1 1 1 1 1 5 1
Correct answer is
7
+++++-+
but your answer is 5.
Correct approach is dynamic programming dp[i][j] — are we able to get number j after i moves.
Thank you.
Try this:
Any ideas for question I please??
Build pairs of < skill, field > for each course, sort all of them in increasing order by skill and find an interval [i, j] of courses which has the following properties:
Thank you!
I would add that you can find such interval in O(n) time using two pointers technique. Of course complexity of whole solution is still O(n log n) because of sorting.
Как решать С?
Мое решение было не "основным", но, как мне кажется, достаточно понятным
Сразу (при чтении) будем формировать отрезки времени, в которые этот коридор свободен — т.е. каждый коридор у нас будет описываться набором свободных отрезков [bj..ej]. Вообще свободный отрезок — важная для нас структура, поэтому, кроме границ отрезка мы будем также хранить в нем самый ранний момент времени, в который мы можем переместиться в коридор ниже. Понятно, что исходно этот момент для всех отрезков будет равен (bj + 1) (на самом деле в структуре в моем решении хранились все моменты перехода, но это уже технические подробности). Для краткости далее я буду говорить о "точках перехода". Достаточно неформально можно понять, что чем левее на отрезке точка перехода, тем он "лучше" — больше возможностей уйти вниз.
Воздушных коридоров (эшелонов, но решили уж избегать этого слова) у нас не очень много — не более 100. Попробуем зафиксировать какой-то коридор в качестве стартового и выясним, в какое самое раннее время мы можем долететь.
Пусть мы зафиксировали коридор #k. Теперь будем двигаться по его свободным отрезкам и — параллельно — по коридору #(k + 1), при необходимости "подклеивая" отрезки коридора #(k + 1) к отрезкам коридора #k (полагаем, что коридор #(k + 1) у нас есть; более того, есть и коридоры еще ниже). Эти "склеенные" отрезки мы будем помещать в новую очередь (список), после чего используем их при рассмотрении коридора #(k + 2).
Когда такая необходимость возникает?
Если рассматриваемый отрезок коридора #k имеет границы bj и ej, точка перехода у него cj (на первом шаге cj = bj + 1, в дальнейшем это может быть не так); рассматриваемый отрезок коридора #(k + 1) имеет границы xi и yi, возможны следующие варианты (рассматривать их нужно последовательно):
А. xi < bj — такой отрезок из коридора #(k + 1) на этом этапе рассматривать не нужно: если даже мы можем перейти из отрезка коридора #k в этот отрезок и впоследствии достичь конечного пункта, при рассмотрении коридора #(k + 1) в качестве стартового этот результат будет неизбежно улучшен.
B. yi ≤ cj — такой отрезок рассматривать нельзя: мы просто не сможем попасть в него из коридора #k (а даже если попадем, то не сможем находиться в коридоре #(k + 1) требуемую единицу времени).
C. bj < xi < cj — в этом случае мы можем спуститься в коридор #(k + 1) в момент cj, так что мы можем сформировать новый отрезок с границами bj и yi и точкой перехода cj + 1. Этот новый отрезок мы поместим в очередь, о которой говорилось выше.
D. cj ≤ xi ≤ ej — в этом случае мы также можем спуститься коридором ниже и сформировать отрезок с границами bj и yi и точкой перехода xi + 1. Этот отрезок мы тоже поместим в очередь.
E. ej < xi — перейти в коридор #(k + 1) нельзя, нужно рассматривать следующий отрезок в коридоре #k.
Таким образом, при проходе по коридорам #k и #(k + 1) мы сформируем новую очередь отрезков, которые упорядочены по левым концам, а при равенстве левых концов — по точкам перехода. Теперь точно так же возьмем за основу полученный набор отрезков и будем двигаться по нему и отрезкам коридора #(k + 2).
Мы будем действовать жадным образом: если есть возможность присоединить какой-то отрезок из #(k + 2) к отрезку из очереди — мы будем это делать (можно показать, что это никогда не ухудшит ответ).
Важный момент: каждый раз, когда мы формируем новый отрезок (стартовый коридор, вероятно, проще рассмотреть отдельно, чем вписывать в изложенную выше схему), мы анализируем, не долетели ли мы еще. Если это так, обновляем ответ (а записывать этот отрезок в очередь уже нет необходимости — лучше результат для него не будет).
Переберем последовательно все коридоры в качестве стартового, получим окончательный ответ.
UPD Асимптотика: .
.
Для каждого коридора (коих n) мы пройдем по всем нижележащим. В силу "жадности" при формировании очереди в ней всегда будет отрезков не более, чем в том коридоре, отрезки которого "подклеиваются", а переберем мы в худшем случае все отрезки всех коридоров по одному разу. Таким образом, оценка —
Ну и собственно код: pastebin
Вначале по поводу WA 17:
При сжатии координат необходимо учитывать не только время открытия/закрытия, но и моменты времени на 100 вперёд. Таким образом, получается порядка 10^8 операций, можно попробовать попихать на плюсах.
Теперь моё решение, которое является основным решением жюри:
Будем идти по коридорам сверху вниз. Для каждого коридора поддерживаем множество непересекающихся отрезков (intervalsi), у каждого отрезка есть следующие свойства: открытие (from) и закрытие (to) отрезка в этом коридоре и минимальное время начала полёта (start), такое, что мы можем попасть на отрезок к моменту его открытия. Также для восстановления ответа можно хранить предка (prev): из какого отрезка мы пришли в данный, либо null если мы начали путешествие из текущего отрезка.
Для первого коридора эти отрезки соответствуют интервалам времени, когда первый коридор открыт. Естественно мы учитываем, что выгодно всегда начинать полёт с какого-либо момента открытия коридора. Также заметим, что полученные отрезки у нас отсортированы по времени их открытия.
Рассмотрим теперь i-й (i > 1) коридор. Мы можем либо начать полёт с этого коридора (опять же, как и в случае с первым коридором, нам выгодно начинать с момента, когда этот коридор открывается), либо перейти в этот коридор с коридора с номером i - 1. Найдём curStarts — все моменты времени, когда мы можем оказаться в данном коридоре (то есть начать полёт с него либо перейти в него). Для того чтобы найти все времена перехода, посмотрим на все возможные пары {отрезок для коридора i - 1, открытый промежуток времени для коридора i} и выберем для каждой пары такой минимальный момент времени (его может и не быть), что мы можем перейти с i - 1-о коридора в i-й (опять же, выбирать минимальный момент времени всегда выгодно). Теперь можно построить на основе curStarts отрезки для i-о коридора, а затем жадно смерджить их следующим образом: если a и b соприкасаются, a.from < b.from и a.start < b.start, то присоединим отрезок b к a — a.to = b.to. Затем, если в каком-то из отрезков мы можем закончить полёт (interval.to - interval.start > = t), то пытаемся обновить результат значением start данного отрезка.
Время работы. На каждом коридоре у нас может добавиться максимум ci отрезков, соответственно максимальное количество отрезков на коридоре равно . Также переход от одного коридора к другому можно делать с помощью двух указателей, поддерживая отсортированность отрезков по времени открытия from. Итого получаем асимптотику
. Также переход от одного коридора к другому можно делать с помощью двух указателей, поддерживая отсортированность отрезков по времени открытия from. Итого получаем асимптотику  .
.
Код: pastebin.
А как насчет одновременно провести онлайн турнир на CodeForces?
Что подразумевается под онлайн турниром? Онсайт был четвертого апреля и только с русскими условиями.
very good problems with nice ideas , but is it necessary that statements be very inexpressive ??
How to solve F?
dp[i][a][b]— the best result foriprocessed indices,aof them are chosen for the first player,bof them — for the second player.There is also a flow solution but DP is much easier.
how is the flow solution modelled ? The DP was pretty easy!
a can be at most 400 and b can be at most 400 and i can be a most 400, a MLE will be given isn't it?
Thanks! I really enjoyed solving your problems! Specially "problem I" which was really interesting in my opinion!
Is it possible to discuss short write ups on the problems? Atleast on the ones with less than 50 AC.
Sorry for my bad English.
C) Main idea: go from up halls to downs and for each hall keep set of disjoint intervals. Interval is a structure with following parameters:
For each hall we can construct its intervals using intevals of previous hall (it is case when we come from up hall) and open segments of current hall (case when we start from that hall). After building intervals for current hall we have to merge them greedily. All that can be done in O(numberOfIntervals) operations if we keep intervals sorted by from and use two pointers. Maximum available value of numberOfIntervals is less or equal than , so we can process all halls with total asymptotic
, so we can process all halls with total asymptotic 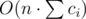 . Further we can find best interval. It is interval with minimal start such that to - start ≥ t. After we just need to restore the answer.
. Further we can find best interval. It is interval with minimal start such that to - start ≥ t. After we just need to restore the answer.
Source: pastebin.
D) I’ll just leave this here: part 5 in article.
E) Just find cutpoints and biconnected components and construct tree of biconnected components. After that we can use dfs on that tree to calculate for each cutpoint sizes of children components and size of parents components. English, Russian. It can be done in O(m) operations.
Source: pastebin.
H) It will be written later by me or elena.
J) In first calculate maxGame – prefix maximum of queries(lengths of games) and sort gamers by t. After that come from the last game to the first and for game number i will be add gamers with t ≥ maxGame[i] in DSU. Answer for game number i: g[i] * size(0), where size(0) — size of set, which contains knight. It also can be solved by BFS and TreeSet. Asymptotic: O(m·α(n)).
Source: DSU, BFS.
some write ups in rev 1.
Enjoyed problem H "A lot of work" a lot. Seems that most of the solutions are some kind of heavy-light decomposition which solves differently long and short colour chains. My solution is a bit different, at least in terms of the written code, there is no distinction between long and short chains, I solve both of them with the same code. The main idea is that the result function for a given colour chain is monotonous with regards to its forgetting parameter k, so if we know that f[k1] = f[k2], then we don't need to calculate the answer in between of k1 and k2. So for a given colour my solution goes as follows:
Submission: 11838173
Code
Your submission is not available for all.
Thanks, always forgetting that submissions in gym are not that easy to see. Plus this time they were submitted with coach mode enabled which makes them even more difficult to see.
And why will we use straightforward approach small amount of times?
Thanks for asking, I forgot to clarify that part. I claim that function f(k) will have no more than distinct values for all given values of k. The reason for that is that we can consider two cases:
distinct values for all given values of k. The reason for that is that we can consider two cases:
So we have distinct values in the result array. The entire point of the algorithm I described above is that it skips intervals where function doesn't change its value. So effectively it looks for all distinct values and then does binary search between adjacent different values to find the exact parameter value where the function changes its value. So in total it should be
distinct values in the result array. The entire point of the algorithm I described above is that it skips intervals where function doesn't change its value. So effectively it looks for all distinct values and then does binary search between adjacent different values to find the exact parameter value where the function changes its value. So in total it should be 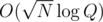 invocations of straightforward algorithm.
invocations of straightforward algorithm.
I think the idea behind heavy-light decomposition in this problem is similar to my intuition above but this solution uses this intuition only to prove its correctness while the code is simply does binary search + brute force approach which is very easy to code, that's why I wanted to share it.
Thanks;)
How to solve problem H by heavy light decomposition ?
Can someone give some tricky test case for problem E ? Thanks I'm not sure if I understand problem E correctly.