gkeesh7's blog

Geometry Problem

By gkeesh7, history, 9 years ago, In English

Greetings Everyone,

I was doing the maximum enclosing circle problem, This is the subproblem of that.

Given two ends points of a common chord of two circles of equal radius say R find out the coordinates of two centers of the circles (without much precision loss preferably)

The condition can be pictorially represented like.

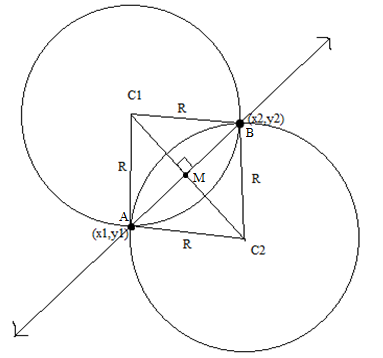
A possible solution might be to find the coordinates of mid point of A and B that is M which is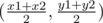

Since the slope of line joining A and B is 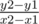and since the line joining the centers would be perpendicular to the slope of line joining C1 and C2 would be .

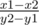The distance between the points M and C1 or C2 can be found using pythagoras theorem i.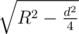e. where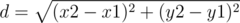

Now since we know the slope of the line and a point on it and distance between the points we can now find the coordinates of centers, but It's highly insensitive to precision.

Any other method, resource , links etc would be deeply appreciated.

Thanks in advance.

  • Vote: I like it
  • +9
  • Vote: I do not like it

Comments Comments (11)
| Write comment?
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Auto comment: topic has been updated by gkeesh7 (previous revision, new revision, compare).

→ Reply
»
9 years ago, # |
← Rev. 7   Vote: I like it 0 Vote: I do not like it

Sorry, my earlier comment is wrong. So we need to find one center, since we know the mid point of the line joining the two centers, we can easily find the second one, once the first one has been found.

For minimizing precision errors, find the length of the perpendicular. Let it be p . Then perform rotation of a point M (xab, yab) either clockwise or anticlockwise. The new coordinate for one center is xc1 = x1cos(x) - y1sin(x) and yc1 = x1sin(x) + y1cos(x).

The trigonometric ratios can be easily found since you know all the sides of the triangle.

Then you can find the other center as you know the coordinate of the midpoint of the line segment joining the two centers ( which is the same as the midpoint of those two initial points)

→ Reply
  • »
    »
    9 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    posted before reading the final revision ignore.

    → Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Can you explain in a bit more detail as to which point you are referring to rotate and rotation is occuring about which point also please specify your notations in your solution. Thanks.

    → Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

One easy idea is to use some affine transformations. First, you can make your points move from (x1,y1) and (x2,y2) to (0,+-a), where 2a — distance between these points. It can be done by simple move by vector (-x1,-y1), then rotation with sin(phi)=c/sqrt(c^2+d^2) (here c=x2-x1, d=y2-y1) and again simple move by vector (0,-a). Now you have a construction where all points belong to axes. And solution is just (+-sqrt(R^2-a^2),0). To obtain a final answer you only need to move and rotate it back. It's easy to get final formulae, there will be only one precision-weak place, sqrt(R^2-a^2), everything is fine. I think, your solution can be simplified to the same operations, it's okay to precision too. One other idea — maybe you can use binary search. But I'm not sure, how precise it can be here.

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Do you mean shifting the origin to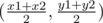 and rotate the coordinate axis by and take the points on the y axis rotate back the coordinate axis by and translate it back to . I will try to do it thanks.

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Yes, smth like that. But keep in mind that you actually don't need angle itself (as atan... or anything), but only its sin() and cos(). It's important to keep precision.

      → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        yes , will you please like to explain your binary search solution.

        → Reply
        • »
          »
          »
          »
          »
          9 years ago, # ^ |
          ← Rev. 2   Vote: I like it 0 Vote: I do not like it

          In binary serch you can use almost anything as a condition =) For example, consider if we are searching for a point on a line, which is orthogonal to line AB and comes through M, with correct distance to A or B. This line equation can be easily found with integer coefficients. It will be in form (x1-x2)*x+(y1-y2)*y+c=0, where c is obtained by substituting point M((x1+x2)/2,(y1+y2)/2) inside. So: 2*(x1-x2)*x+2*(y1-y2)*y+((x2^2-x1^2)+(y2^2-y1^2))=0, correct me if I'm wrong. And here we can use binary search: take x=(x1+x2)/2..INF; then find corresponding y from equation of the line; check if distance between (x,y) and A (or B) is equal to R with enough precision. Second center can be obtained from the fact, that M is a middle of C1C2.

          → Reply
»
9 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

As an alternative way ,we can apply Binary Search . Assume 2 line segments,each with 1 of their end point as A (& for other segment B) . Assign initial direction arbitrarily to each of them that are not same (one anti-clockwise then other clockwise). Our condition for binary search being whether two line segments intersect or not which can be done in constant time . We keep initial difference between typical hi , lo variables of BS at say 90 degrees .If true we move segments in their respective directions ,if not we swap their direction before moving to their respective mid .

I suppose we can reach precision saturation of storage type in some thousand iterations :) (Correct me if i am wrong here)

Also can you link the original problem you were solving?

→ Reply
  • »
    »
    9 years ago, # ^ |
    ← Rev. 9   Vote: I like it 0 Vote: I do not like it

    I was doing this problem set from gym, Local Contest , The problem is Party Location, I read this quora thread for the approach (from chhung6's answer ). since n <  = 200 O(n3) is probably fine for the problem

    → Reply