Добрый вечер!
Недавно я столкнулся со следующей проблемой: в процессе решения некой задачи мне понадобилось считать определитель достаточно специфичной матрицы:
1) Ее размер может быть до 600.
2) Все ее элементы — целые числа из множества { - 1, 0, 1}.
3) В любой ее строке и столбце не более 4 ненулевых элементов — то есть, она сильно разрежена (вообще говоря, это матрица смежности некого двудольного графа, но некоторые ребра взяты с минусом).
Притом определители надо подсчитать приблизительно у сотни таких матриц.
Я скопировал код с e-maxx.ru, и переписал все на Java, но сомневаюсь в эффективности полученного кода. Детерминант, очевидно, может быть очень большим, из-за чего приходится пользоваться BigDecimal и BigInteger с округлениями. По всем этим причинам код работает жутко медленно и нуждается в оптимизации.
public static BigInteger determinant(final int[][] matr) {
int accuracy = 20;
BigDecimal EPS = BigDecimal.valueOf(0.00000000001);
int n = matr.length;
BigDecimal[][] a = new BigDecimal[n][n];
for (int i = 0; i < n; ++i)
for (int j = 0; j < n; ++j) {
a[i][j] = new BigDecimal(matr[i][j]);
a[i][j].setScale(accuracy, BigDecimal.ROUND_HALF_UP);
}
BigDecimal det = new BigDecimal(1.0);
det.setScale(accuracy, BigDecimal.ROUND_HALF_UP);
for (int i = 0; i < n; ++i) {
int k = i;
for (int j = i + 1; j < n; ++j)
if (a[j][i].abs().compareTo(a[k][i].abs()) > 0)
k = j;
if (a[k][i].abs().compareTo(EPS) < 0) {
det = new BigDecimal(0.0);
det.setScale(accuracy, BigDecimal.ROUND_HALF_UP);
break;
}
BigDecimal[] tmp = a[i];
a[i] = a[k];
a[k] = tmp;
if (i != k)
det = det.divide(new BigDecimal(-1), accuracy, BigDecimal.ROUND_HALF_UP);
det = det.multiply(a[i][i]);
for (int j = i + 1; j < n; ++j)
a[i][j] = a[i][j].divide(a[i][i], accuracy, BigDecimal.ROUND_HALF_UP);
for (int j = 0; j < n; ++j)
if (j != i && a[j][i].abs().compareTo(EPS) > 0)
for (int kk = i + 1; kk < n; ++kk) {
BigDecimal aikji = new BigDecimal(1.0);
aikji.setScale(accuracy, BigDecimal.ROUND_HALF_UP);
aikji = aikji.multiply(a[i][kk]);
aikji = aikji.multiply(a[j][i]);
aikji = aikji.multiply(new BigDecimal(-1));
a[j][kk] = a[j][kk].add(aikji);
}
}
det = det.abs();
det = det.add(new BigDecimal(0.00001));
return det.abs().toBigInteger();
}
На Java я начал писать сравнительно недавно, и, возможно, упускаю какие-то моменты для оптимизации. Может ли кто-нибудь дать совет по коду, или привести ссылку на уже реализованный оптимизированный алгоритм?
UPD. Из всех предложенных вариантов подошел следующий: так как для матрицы размера N × N ответ не превосходит 2N, то можно привести матрицу к верхнетреугольному виду, выполняя все вычисления по модулю prime, где prime — простое число битовой длины не менее N — найти его помогут встроенные функции BigInteger. Скорость по сравнению с реализацией на BigDecimal возросла чуть ли не в десяток раз.
Вот такие картинки получились благодаря алгоритму (увы, смазанные на этом сайте) :)
Код, если кому-то будет интересен:
public static BigInteger determinant(final int[][] matr) {
int n = matr.length;
BigInteger[][] a = new BigInteger[n][n];
for (int i = 0; i < n; ++i) {
for (int j = 0;j < n; ++j) {
a[i][j] = BigInteger.valueOf(matr[i][j]);
}
}
BigInteger prime = BigInteger.probablePrime(n + 4, new Random());
BigInteger det = BigInteger.ONE;
for (int row = 0; row < n; ++row) {
int currentRow = row;
while (currentRow < n && a[currentRow][row].equals(BigInteger.ZERO)) {
++currentRow;
}
if (currentRow == n) {
return BigInteger.ZERO;
}
if (currentRow != row) {
det = det.negate();
BigInteger[] tmp = a[currentRow];
a[currentRow] = a[row];
a[row] = tmp;
}
BigInteger inverse = a[row][row].modInverse(prime);
for (currentRow = row + 1; currentRow < n; ++currentRow) {
if (a[currentRow][row].equals(BigInteger.ZERO)) {
continue;
}
BigInteger coefficient = a[currentRow][row].multiply(inverse).remainder(prime);
for (int column = row; column < n; ++column) {
a[currentRow][column] = a[currentRow][column].subtract(a[row][column].multiply(coefficient).remainder(prime)).remainder(prime);
}
}
}
for (int i = 0; i < n; ++i) {
det = det.multiply(a[i][i]).remainder(prime);
}
det = det.add(prime);
det = det.remainder(prime);
if (det.multiply(BigInteger.valueOf(2)).compareTo(prime) > 0) {
det = prime.subtract(det).remainder(prime);
}
return det;
}











Можно посчитать по простым модулям и восстановить по КТО. Думаю будет быстрее. (Нужно только оценить максимальный ответ и взять достаточно модулей.
BigDecimal'ы определенно не нужны. Пусть нам нужно обработать очередной столбец, тогда добавляем строки по одной, выполняем на них алгоритм евклида по первым элементам. Первый элемент одной из них зануляется.
Спасибо за совет, буду переписывать на Евклида в Integer'ах)
По-моему, гораздо красивее, легче и быстрее будет привести матрицу к треугольному виду за O(N^3), причём ничего выходящего за пределы int-a не должно получиться при преобразовании, а затем перемножить элементы главной диагонали. Либо, раз матрица кишит нулями, можно попробовать посчитать методом Лапласа, но я всё же склоняюсь к приведению к треугольному виду.
Не тривиально, что переполнений не будет.
Но ведь элементы матрицы только 0, 1 и -1. При преобразовании надо будет только складывать и вычитать строки без умножения их на что-то большее единицы. Тогда в худшем случае в некоторой строке может получиться элемент порядка N^2, но, учитывая ограничения, это не больше 360000.
После того, как один раз добавить элементы уже не будут единичными и поэтому возможно умножение на что-то большее.
2N × 2N, det = 2N
Есть примеры, где у матриц n × n определитель имеет порядок 2n. Если уж на то пошло, то в алгоритме определитель матрицы — это количество максимальных паросочетаний в некотором двудольном графе и метод Лапласа просто будет брать какую-то пару, уменьшая двудольный граф. А с треугольной матрицей спасибо за идею, действительно, можно не выходить из Integer.
Если хотите развлечься, вот обзор алгоритмов решения этой задачи: http://www4.ncsu.edu/~kaltofen/bibliography/02/KaVi02.pdf
Ну и создавать объекты в самом вложенном месте я бы не стал(особенно всегда одинаковые).
1 = BigDecimal.ONE, вместо умножения на -1 negate()
Автокомментарий: текст был обновлен пользователем Neodym (предыдущая версия, новая версия, сравнить).
А как вы получили оценку в 2n на определитель такой матрицы? Я умею только n! и 4n, но это совсем простые.
Эта оценка утверждается не для всех матриц, а только для полученных специальным образом.
Берется клеточная фигура, разбивается на черные и белые клетки, по ним строится двудольный граф (ребра соединяют соседние черные и белые клетки). Для этого графа строится матрица смежности, притом вместо некоторых единичек стоят минус единички так, что определитель матрицы равен количеству способов разбить исходную фигуру на доминошки. Если матрица имеет размеры N × N, то площадь фигуры 2N, а количество доминошек в разбиении — N. Из этого легко вывести, что определитель (т.е. число разбиений) не превосходит 2N (в духе: рассмотрим уголок фигуры, там доминошка может располагаться не более чем 2 способами, выкинем ее, рассмотрим оставшееся и т.д.).
Хм, оказывается, это верно для всех матриц, где любая строка содержит только целые числа из множества { - 1, 0, 1}, притом ненулевых не более 4. Заметим, что строки матрицы задают N векторов в N-мерном Евклидовом пространстве, длина каждого из которых не превосходит . Определитель — это обьем фигуры, натянутой на эти векторы, как мы помним из линейной алгебры, он не превосходит произведения длин всех векторов, что в свою очередь не превосходит 2N.
. Определитель — это обьем фигуры, натянутой на эти векторы, как мы помним из линейной алгебры, он не превосходит произведения длин всех векторов, что в свою очередь не превосходит 2N.
Есть намного более быстрое решение, не использующее O(N^3) взятий остатка по огромному модулю.
Пусть мы в данный момент зануляем нижнюю часть i-го столбца. Без потери общности считаем, что M[i][i] != 0. Допустим, мы хотим занулить M[j][i]. Так давайте же запустим нерекурсивный расширенный алгоритм Евклида на элементах M[i][i] и M[j][i].
Алгоритм найдет, во-первых, разложение для gcd(M[i][i], M[j][i]), во-вторых, нетривиальное разложение для нуля. Запишем все это для наглядности в матричной форме: .
.
Думаю, из всего вышенаписанного уже очевидно, что делать с i-й и j-й строкой. Теперь нужно понять, что произойдет с определителем. Как ни странно, он домножится на (тривиально доказывается через теорему Лапласа). Можно заметить, что определитель останется без изменения при четном количестве итераций алгоритма Евклида и изменит знак при нечетном количестве итераций — так можно вообще обойтись без знания теоремы Лапласа.
(тривиально доказывается через теорему Лапласа). Можно заметить, что определитель останется без изменения при четном количестве итераций алгоритма Евклида и изменит знак при нечетном количестве итераций — так можно вообще обойтись без знания теоремы Лапласа.
Если не хочется писать лишний код, а таймлимит позволяет — можно непосредственно вычитать строки внутри алгоритма Евклида. Кажется, именно про это и писал выше riadwaw.
P.S. Идею о нерекурсивном алгоритме Евклида и о вычислении определителя целиком в целых числах я услышал от zeliboba в далеком 2012 году.
P.P.S. Прошу прощения за сумбурный текст, но я уже хочу спать. По той же причине я написал код на C++.
Как я понимаю, вы предлагаете делать такую операцию со строками:
M[i] = x1M[i] + y1M[j]
M[j] = x2M[i] + y2M[j]
Но оставшиеся числа в строках в результате такой операции могут очень сильно увеличиться (их битовая длина станет гораздо больше N). Я уже пробовал делать с помощью алгоритма Евклида и эти операции вызывали StackOverFlowError.
Польза от использования простого модуля оказалась именно в том, что в процессе обработки битовая длина любого элемента матрицы не превосходит одного и того же значения.
Такая себе идея — писать алгоритм Евклида рекурсивно, когда стек размером 1МБ, а числа большие.
Я пару дней назад как раз реализовал на Java все то, что описано в моем предыдущем комментарии — и да, большие числа сильно портят всю малину :(. Определитель матрицы 80х80 считался несколько часов, и программа отжирала больше полутора гигабайт ОЗУ.
А вообще, самое быстрое, что я знаю — это как раз подсчет определителя по энному количеству простых модулей размера порядка квадратного корня из 10^9 и восстановление ответа по КТО. Тогда получается, что непосредственно в алгоритме Гаусса все взятия по модулю будут производиться строго над интами. И да, эту идею мне рассказал все тот же Ренат Гимадеев.
То есть вы считаете, что выгоднее считать определитель не один раз по модулю длины N, а N / 4 раз считать определитель по модулю int? Подсчет сложностей говорит, что их отношение будет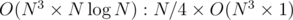 — сложность умножения чисел длины N против соответственных операций в интах , что как будто бы выгоднее, но верится с трудом:)
— сложность умножения чисел длины N против соответственных операций в интах , что как будто бы выгоднее, но верится с трудом:)
Числа в стандартной библиотеке умножаются за порядка N^2/C, а не за NlogN, я думаю.
И да, я думаю много модулей будет прилично быстрее. (Хотя я бы скорее брал модулю около 10^9 и считал в long)
На 32-битной архитектуре это точно в разы медленнее. На 64-битной я не тестировал.
Видимо, все-таки быстрее, потому что для матрицы размера 1250 переписывание на КТО по 170 модулям не принесло существенного выигрыша — а даже наоборот ухудшило ситуацию:(
А можно посмотреть код с КТО?
http://pastie.org/10358524#1,47
Как оказалось, проблема заключается не в том, что переписывание на int плохо ускоряет вычисления, а в том, что эти самые вычисления вызываются довольно редко. Например, для матрицы 650 × 650 операция "отнять одну строку от другой" вызывается 8125 раз, а для матрицы 1250 × 1250 — 30345 раз (потому как матрица сильно разрежена, в некоторых строках полно нолей и можно не отнимать от таких строк ничего)
Эти величины далеки от квадратичных (больше похожи на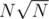 ), и сложность вычисления детерминанта для данной конкретной задачи выглядит как
), и сложность вычисления детерминанта для данной конкретной задачи выглядит как  , где mult — сложность умножения двух чисел.
, где mult — сложность умножения двух чисел.
Ну, а от эн-куб уже вряд ли можно как-то избавиться=)