Уважаемые КФ-цы! Сегодня прошла 2 командная олимпиада на сайте http://acmp.ru/asp/champ/index.asp?main=tasks&id_stage=40501 (Ссылка на условия). Может кто нибудь подскажет как правильно решать задачи В (Деление) и Н (Паутина). Спасибо.
→ Обратите внимание
До соревнования
Rayan Programming Contest 2024 - Selection (Codeforces Round, Div. 1 + Div. 2)
5 дней
Зарегистрироваться »
Rayan Programming Contest 2024 - Selection (Codeforces Round, Div. 1 + Div. 2)
5 дней
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 156 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 10 | nor | 152 |
→ Найти пользователя
→ Прямой эфир
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 25.11.2024 21:09:01 (k1).
Десктопная версия, переключиться на мобильную.
При поддержке
Задачу B мы решали следующим образом: брали точку центра и строили прямые через нее и все остальные по очереди. Каждый раз проходили по всем точкам, отмечая, с какой стороны от прямой они лежат. Если точка лежала на прямой, то смотрели еще относительно прямой, перпендикулярной первой. Ну и если ответ существовал, то либо все точки лежат по одну сторону от первой прямой, либо если встретились точки на ней, то смотрели на результаты второй. // Правда сдать так и не успели
В H просто сортировали по убыванию высот и проходили по каждому горизонтальному отрезку, пересекающему текущую позицию.
Так а где уверенность, что она у Вас правильно решена, если не успели сдать. Я тоже проводил вертикальную прямую и горизонтальную, которые делили квадрат на два прямоугольника одинаковой площади и считал точки, все ли с одной стороны от прямой. Но разрез может быть произвольным. Так я двигал точки с шагом по противоположным сторонам квадрата, по одной стороне вниз, по второй вверх. Строил прямые и считал для каждой прямой расположение точек. WA 15 вышло. По сторонам ходил с шагом 1, и 0,1, и 0,01 и ничего не вышло.
Уверенности никакой и нет, вот была б дорешка...
Мы предполагали, что разрез пройдет бесконечно близко к одной из точек, поэтому и проводили через каждую. Из-за этого приходилось использовать перпендикулярную прямую. Типа можно подвинуть эту прямую на бесконечно малое расстояние при двух точках, лежащих на самой прямой, если они лежат по одну сторону от центра.
Вот как раз в проверке все ли точки лежат с одной стороны от прямой и была у меня ошибка.Очень маленькая погрешность. И все время выдавало, что точка не лежит на прямой. Никак не удалось избавиться этой ошибки. А может есть какое то другое , более оригинальнее решение?
Мы использовали проверку с погрешностями дабы избежать такого.
Вполне возможно, что есть и что-нибудь другое...
Дорешка есть!
Не подскажешь тогда, где она?
A B C D Е F G H
Ну да, не все есть(4/8) =(
По крайней мере задача H это боян. Паутина
А еще нам ее на город давали) В 2012 или 2013
Если она баян, то где можно увидеть решение?
Вот держи, например, только что заслал http://pastebin.com/yQpcU7hY
Я не участвовал, но могу предложить решение задачи B:
Скажем, что разрез можно провести от центра до какой-нибудь свечи. Возьмем вектор от центра квадрата до свечи. Теперь как проверить с какой стороны лежит свеча? Возьмем вектор от центра до выбранной свечи и посмотрим на векторное произведение (ax * by - ay * bx) — значение <0 для одной половины и >=0 для другой.
Проверим, что мы можем найти разрез, для которого количество свечей на любой из сторон равно 0 ( UPD: лучше просто посмотреть, что все векторные произведения одного знака). Асимптотика — O(M2)
Так как делений нет, все операции можно делать в целых числах => нет проблем с точностью. Извиняюсь, если я неправ)
Там есть небольшая проблема с тем, что нельзя резать по свечам, т.е. диаметр у них не нулевой. Соответственно, тест типа такого не будет корректно отрабатывать.
4 2
1 3
3 1
NO
А центр, кстати, может стать нецелым числом, если сторона нечетной длины
Насчет центра — домножим все координаты на 2 и проблема решена)
Насчет разреза — можно попробовать взять +-eps=1e-9, тогда никакая свеча не будет лежать на разрезе (по условию — свечи можно считать точками)
С центром соглашусь. На вторую же поправку держи еще контрпример
5 2
4 4
3 3
YES
Вот нашел словесное решение задачи http://algolist.manual.ru/olimp/geo_prb.php#z20
Упс. Действительно, если есть векторное произведение равное 0, то разрез не подходит. )
Ну вроде все работает, нет?
Векторы — (-0.5; -0.5 + eps) и (-1.5; -1.5). Векторные произведения одного знака или 0. Все нормально. Или я что-то упускаю?)
Как решать G?
А я тогда заодно спрошу еще нормальное решение Е. Мы таких там костылей понаставили, что мне аж стыдно, что зашло
Посчитаем факториалы всех чисел от 1 до 100000 по модулям 109 + 7 и 109 + 9, посчитаем число из инпута по тем же модулям.
Похоже, что факториал числа по простому модулю ведёт себя достаточно случайно, поэтому коллизии начинаются в районе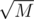
, как и говорит нам парадокс дней рождения. Забавный факт.
Ох, действительно, так было значительно проще... Удивлен даже, что не дошли до этого на контесте.
Спасибо
Задачу В решал так: Что бы разрезать торт на 2 равные части, линия разреза обязательно пройдет через центр торта. Тогда переберем все прямые проходящие через центр: будем строить прямую по двум точкам, одна из которых в центре квадрата, а вторая находится на (допустим) нижней стороне.
Координаты первой точки n / 2, n / 2.
Координаты второй точки i, 0, где i перебираем от 0 до n c шагом 0.01.
Для каждой прямой смотрим не проходит ли она через свечку и сколько свечек находится под прямой и над прямой. Если нашли ситуацию, когда все условия выполняются выводим YES.
P.S. Да, решение через double, поэтому могли возникнуть проблемы с точностью. Но тем не менее зашло с первого раза=)