Div.2 A (Author: Haghani)
Idea is a simple greedy, buy needed meat for i - th day when it's cheapest among days 1, 2, ..., n.
So, the pseudo code below will work:
ans = 0
price = infinity
for i = 1 to n
price = min(price, p[i])
ans += price * a[i]

Time complexity: 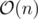
Div.2 B (Author: PrinceOfPersia)
Find all prime divisors of n. Assume they are p1, p2, ..., pk (in 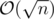 ). If answer is a, then we know that for each 1 ≤ i ≤ k, obviously a is not divisible by pi2 (and all greater powers of pi). So a ≤ p1 × p2 × ... × pk. And we know that p1 × p2 × ... × pk is itself lovely. So,answer is p1 × p2 × ... × pk
). If answer is a, then we know that for each 1 ≤ i ≤ k, obviously a is not divisible by pi2 (and all greater powers of pi). So a ≤ p1 × p2 × ... × pk. And we know that p1 × p2 × ... × pk is itself lovely. So,answer is p1 × p2 × ... × pk

Time complexity: 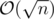
A (Author: PrinceOfPersia)
Problem is: you have to find the minimum number of k, such there is a sequence a1, a2, ..., ak with condition 2a1 + 2a2 + ... + 2ak = S = 2w1 + 2w2 + ... + 2w2. Obviously, minimum value of k is the number of set bits in binary representation of S (proof is easy, you can prove it as a practice :P).

Our only problem is how to count the number of set bits in binary representation of S? Building the binary representation of S as an array in 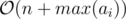 is easy:
is easy:
MAXN = 1000000 + log(1000000)
bit[0..MAXN] = {} // all equal to zero
ans = 0
for i = 1 to n
bit[w[i]] ++ // of course after this, some bits maybe greater than 1, we'll fix them below
for i = 0 to MAXN - 1
bit[i + 1] += bit[i]/2 // floor(bit[i]/2)
bit[i] %= 2 // bit[i] = bit[i] modulo 2
ans += bit[i] // if bit[i] = 0, then answer doesn't change, otherwise it'll increase by 1
Time complexity: 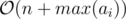
B (Author: PrinceOfPersia)
If we fix x and bix mod n, then problem will be solved (because we can then multiply it by the number of valid distinct values of 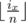 ).
).
For the problem above, let dp[i][j] be the number of valid subsequences of b where x = j and 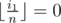 and
and 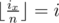 . Of course, for every i, dp[i][1] = 1. For calculating value of dp[i][j]:
. Of course, for every i, dp[i][1] = 1. For calculating value of dp[i][j]:
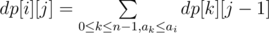
For this purpose, we can sort the array a and use two pointer:
if p0, p1, ...pn - 1 is a permutation of 0, ..., n - 1 where for each 0 ≤ t < n - 1, apt ≤ apt + 1:
for i = 0 to n-1
dp[i][1] = 1
for j = 2 to k
pointer = 0
sum = 0
for i = 0 to n-1
while pointer < n and a[p[pointer]] <= a[i]
sum = (sum + dp[p[pointer ++]][j - 1]) % MOD
dp[i][j] = sum

Now, if 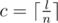 and x = l - 1 mod n, then answer equals to
and x = l - 1 mod n, then answer equals to 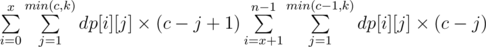 (there are c - j + 1 valid different values of
(there are c - j + 1 valid different values of 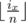 for the first group and c - j for the second group).
for the first group and c - j for the second group).
Time complexity: 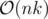
C (Author: PrinceOfPersia)
Solution is something like the fourth LCA approach discussed here.
For each 1 ≤ i ≤ n and 0 ≤ j ≤ lg(n), store the minimum 10 people in the path from city (vertex) i to its 2j - th parent in an array.
Now everything is needed is: how to merge the array of two paths? You can keep the these 10 values in the array in increasing order and for merging, use merge function which will work in 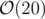 . And then delete the extra values (more than 10).
. And then delete the extra values (more than 10).
And do the same as described in the article for a query (just like the preprocess part).

Time complexity: 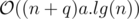
D (Author: PrinceOfPersia)
Run binary search on the answer (t). For checking if answer is less than or equal to x (check(x)):
First of all delete all edges with destructing time greater than x. Now, if there is more than one pair of edges with the same color connected to a vertex(because we can delete at most one of them), answer is "No".
Use 2-Sat. Consider a literal for each edge e (xe). If xe = TRUE, it means it should be destructed and it shouldn't otherwise. There are some conditions:
For each vertex v, if there is one (exactly one) pair of edges like i and j with the same color connected to v, then we should have the clause
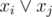 .
.For each vertex v, if the edges connected to it are e1, e2, ..., ek, we should make sure that there is no pair (i, j) where 1 ≤ i < j ≤ k and xe1 = xe2 = True. The naive approach is to add a clause
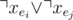 for each pair. But it's not efficient.
for each pair. But it's not efficient.

The efficient way tho satisfy the second condition is to use prefix or: adding k new literals p1, p2, ..., pk and for each j ≤ i, make sure 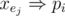 . To make sure about this, we can add two clauses for each pi:
. To make sure about this, we can add two clauses for each pi: 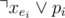 and
and 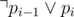 (the second one is only for i > 1).
(the second one is only for i > 1).
And the only thing left is to make sure 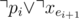 (there are no two
(there are no two TRUE edges).
This way the number of literals and clauses are 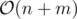 .
.
So, after binary search is over, we should run check(t) to get a sample matching.
Time complexity: 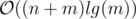 (but slow, because of the constant factor)
(but slow, because of the constant factor)
E (Authors: PrinceOfPersia and Haghani)
Lemma #1: If numbers b1, b2, ..., bk are k Kheshtaks of a1, ..., an, then  is a Kheshtak of a1, ..., an.
is a Kheshtak of a1, ..., an.
Proof: For each 1 ≤ i ≤ k, consider maski is a binary bitmask of length n and its j - th bit shows a subsequence of a1, ..., an (subset) with xor equal to bi.
So, xor of elements subsequence(subset) of a1, ..., an with bitmask equal to 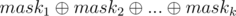 equals to
equals to  . So, it's a Kheshtak of this sequence.
. So, it's a Kheshtak of this sequence.
From this lemma, we can get another results: If all numbers b1, b2, ..., bk are k Kheshtaks of a1, ..., an, then every Kheshtak of b1, b2, ..., bk is a Kheshtak of a1, ..., an
Lemma #2: Score of sequence a1, a2, ..., an is equal to the score of sequence 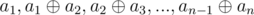 .
.
Proof: If we show the second sequence by b1, b2, ..., bn, then for each 1 ≤ i ≤ n:
- bi =
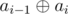
- ai =

 each element from sequence b is a Kheshtak of sequence a and vise versa. So, due to the result of Lemma #1, each Kheshtak of sequence b is a Kheshtak of sequence a and vise versa. So:
each element from sequence b is a Kheshtak of sequence a and vise versa. So, due to the result of Lemma #1, each Kheshtak of sequence b is a Kheshtak of sequence a and vise versa. So:
- score(b1, ..., bn) ≤ score(a1, ..., an)
- score(a1, ..., an) ≤ score(b1, ..., bn)
 score(a1, ..., an) = score(b1, ..., bn)
score(a1, ..., an) = score(b1, ..., bn)

Back to original problem: denote another array b2, ..., bn where 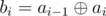 . Let's solve these two problems:
. Let's solve these two problems:
1- We have array a1, ..., an and q queries of two types:
- upd(l, r, k): Given numbers l, r and k, for each l ≤ i ≤ r, perform
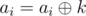
- ask(i): Given number i, return the value of ai.
This problem can be solved easily with a simple segment tree using lazy propagation.
2- We have array b2, ..., bn and queries of two types:
- modify(p, k): Perform bp = k.
- basis(l, r): Find and return the basis vector of bl, bl + 1, ..., br (using Gaussian Elimination, its size it at most 32).
This problem can be solved by a segment tree where in each node we have the basis of the substring of that node (node [l, r) has the basis of sequence bl, ..., br - 1).
This way we can insert to a basis vector v:
insert(x, v)
for a in v
if a & -a & x
x ^= a
if !x
return
for a in v
if x & -x & a
a ^= x
v.push(x)
But size of v will always be less than or equal to 32. For merging two nodes (of segment tree), we can insert the elements of one in another one.
For handling queries of two types, we act like this:
Type one: Call functions: upd(l, r, k), 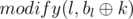 and
and 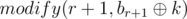 .
.
Type two: Let b = basis(l + 1, r). Call insert(al, b). And then print 2b.size() as the answer.
Time complexity: 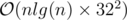 =
= 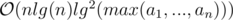
F (Author: PrinceOfPersia)
Use Aho-Corasick. Assume first of all we build the trie of our strings (function t). If t(v, c) ≠ - 1 it means that there is an edge in the trie outgoing from vertex v written c on it.
So, for building Aho-Corasick, consider f(v) = the vertex we go into, in case of failure (t(v, c) = - 1). i.e the deepest vertex (u), that v ≠ u and the path from root to u is a suffix of path from root to v. No we can build an automaton (Aho-Corasick), function g. For each i, do this (in the automaton):
cur = root
for c in s[i]
cur = g(cur, c)
And then push i in q[cur] (q is a vector, also we do this for cur = root).
end[cur].push(i) // end is also a vector, consisting of the indices of strings ending in vertex cur (state cur in automaton)
last[i] = cur // last[i] is the final state we get to from searching string s[i] in automaton g
Assume cnt(v, i) is the number of occurrences of number i in q[v]. Also, denote 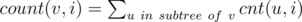 .
.
Build another tree. In this tree, for each i that is not root of the trie, let par[i] = f(i) (the vertex we go in the trie, in case of failure) and call it C-Tree.
So now, problem is on a tree. Operations are : Each query gives numbers l, r, k and you have to find the number 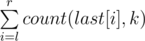 .
.

Act offline. If N = 105, then:
1. For each i such that 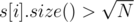 , collect queries (like struct) in a vector of queries query[i], then run
, collect queries (like struct) in a vector of queries query[i], then run dfs on the C-Tree and using a partial sum answer to all queries with k = i. There are at most  of these numbers, so it can be done in
of these numbers, so it can be done in 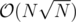 . After doing these, erase i from all q[1], q[1], ..., q[N].
. After doing these, erase i from all q[1], q[1], ..., q[N].
Code (in dfs) would be like this(on C-Tree):
partial_sum[n] = {}; // all 0
dfs(v, i){
cnt = 0;
for x in q[v]
if(x == i)
++ cnt;
for u in childern[v]
cnt += dfs(u);
for x in end[v]
partial_sum[x] += cnt;
return cnt;
}
calc(i){
dfs(root, i);
for i = 2 to n
partial_sum[i] += partial_sum[i-1]
for query u in query[i]
u.ans = partial_sum[u.r] - partial_sum[u.l - 1]
}
And we should just run calc(i) for each of them.
2. For each i such that 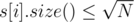 , collect queries (like struct) in a vector of queries query[i]. (each element of this vector have three integers in it: l, r and ans).
, collect queries (like struct) in a vector of queries query[i]. (each element of this vector have three integers in it: l, r and ans).
Consider this problem:
We have an array a of length N(initially all element equal to 0) and some queries of two types:
- increase(i, val): increase a[i] by val
- sum(i): tell the value of a[1] + a[2] + ... + a[i]
We know that number of queries of the first type is 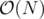 and from the second type is
and from the second type is 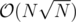 . Using Sqrt decomposition, we can solve this problem in
. Using Sqrt decomposition, we can solve this problem in 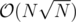 :
:
K = sqrt(N)
tot[K] = {}, a[N] = {} // this code is 0-based
increase(i, val)
while i < N and i % K > 0
a[i ++] += val
while i < K
tot[i/K] += val
i += K
sum(i)
return a[i] + tot[i/K]
Back to our problem now.
Then, just run dfs once on this C-Tree and act like this:
dfs(vertex v):
for i in end[v]
increase(i, 1)
for i in q[v]
for query u in query[i]
u.ans += sum(u.r) - sum(u.l - 1)
for u in children[v]
dfs(u)
for i in end[v]
increase(i, -1)
Then answer to a query q is q.ans.
Time complexity: 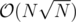












Auto comment: topic has been updated by PrinceOfPersia (previous revision, new revision, compare).
Fastest editorials till date :)
Is there any faster solution for problem F?
What's wrong in this solution? Let's build suffix array for the string s1 + '# + s2 + ... + sn, then lcp array for this suffix array. For the given query (k, l, r) we are interested in suffixes which have lcp >= length(s[k]) with our string. We can find them using binary search. They will form a segment in this array. Then we need to cound amount of number l <= x[i] <= r in this segment, where x[i] is the index of string of the i-th suffix. It can be done with segment tree storing for each node sorted subarray of x. It seems to work in O(N * log^2(N)).
It seems that you misunderstood problem statement...
Yeah I thought we find occurences of given string to other strings sorry:(
C was kinda much easier compared to B... What ya think?
...
Isn't Duff a girl?
WOW :D Thanks for the super fast editorial :D ^_^ PrinceOfPersia
I think i am doing exactly as the editorial for question div2-D/div1-B.
Can someone help me find the mistake ?
http://ideone.com/S98N8o
Your editorials are so nice to read :)
My solution for F in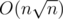 as well but it uses another idea. I split strings in blocks of
as well but it uses another idea. I split strings in blocks of 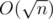 string each. Then for each block I build Aho-Corasick and using this data I count how many times strings from block occur in sk. And also manually check corner strings.
string each. Then for each block I build Aho-Corasick and using this data I count how many times strings from block occur in sk. And also manually check corner strings.
My AC solution: 13648193
Fastest Editorial ever, thank to PrinceOfPersia
div2E/div1C can also be solved using Centroid Decomposition. For each level of the centroid tree, I maintain
int d[LOGN][N][10]
// d[i][j] stores the 10 minimum vertices on path from root till j in the i'th level of decomposition.
Now for each query u,v. I find it's LCA in centroid tree.Let level of LCA be "lvl". Answer would be a minimum vertices in the combined array of d[lvl][u] and d[lvl][v].
See this code for better understanding http://mirror.codeforces.com/contest/588/submission/13641078
In problem D:
When you add two clauses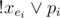 and
and 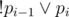 , how can you avoid the case where both xei and pi is false but pi is true?
, how can you avoid the case where both xei and pi is false but pi is true?
Another way to solve Div 2/C is by using map , Reason: two numbers a&b : 2^a + 2^b= 2^x then a=b; here is the soln —
http://ideone.com/carXAR
This solution is absolutely the same, but it uses a map instead of an array, so you get O(n * log(n)). Good solution.
Thnx MistaFrosty , but space complexity is less for this soln..
div1b
"For the problem above, let dp[i][j] be the number of valid subsequences of b where x=j and floor(i_1/n) = 0 and floor(i_x/n) = i"
isn't it supposed to be like x=i and floor(i_x/n) = j?
any prove for B div2 ?? it's not clear for me :/
Well lets present N like N = p[1] ^ a[1] * p[2] ^ a[2] * ... * p[k] ^ a[k]; So any divisor of N can be presented like p[1] ^ s[1] * p[2] ^ s[2] * ... * p[k] ^ s[k], where 0 <= s[i] <= a[i]. So if we try to maximize the answer we should make s[i] as much as possible but we cant make any s[i] > 1, because then our 'answer' would be divisible by p[i] * p[i]. That's why the actual answer is p[1] * p[2] * ... * p[k]
I understand thank you :D i.trofimow
I used persistent segment tree for Div2 E, so,no merging is needed here,simply build the tree in less than 10 lines of code and query for your answer in 4 lines :) A nice problem to solve during contest...
and I implemented 300++ lines of code in virtual contest , and still couldn't solve it :|
Were there large random tests in E? I've tested my solution on one of them during the round, the first submission worked in 6.7s, so I decided to optimize it, and the third submission ran in 5.5s on that test. And I was quite surprised to see that my solution has maximal time 3.8s, so I think my first submission was AC too.
My solution worked in 9s locally against ~6s on CF, and about the same time ratio for solution of C. I blame system performance difference.
Yes, these were times on custom invocation on CF. Locally it ran about 8s in the beginning, and the last version worked in 6.2s.
Any comments from administration? It seems that custom invocation doesn't show the right time the solution runs on system tests, I think it's quite important issue.
If your soluion got TL then it will rerun on free core with high priority several times. So if your solution got AC, the value of running time maybe incorrect. But if you got TL, you can be sure that your solution actually works slow.
P.S.: Thanks for -100 with #define int long long.
P.S.2: I'm not administration, so information can be wrong.
I don't think that's the case: TL is 7s, and the running time of the solution is 3.4s. Also I chcked that test generation works in 358ms, so it shouldn't have affected the running time much.
P.S. Sorry for that, I almost always use it, when seeing a problem involving long long-s.
Div1A/Div2C was fun. Which should be the approach if the subsequences must be contiguous? I was struggling with this question before the clarification
The artwork was wonderful as always!
Can somebody explain how the function insert(x, v) works in the question E of Div 1?
Thanks for Python Code for Div2 A, B :D
Div1 C is identical to a problem on SPOJ 3 years ago which requires a O(qlogn) solution. It seems that many guys just submitted their SPOJ code to get over this prob lol.
Div 2 E can be solved with persistent segment tree aa well . solution
I also did Persistent. Here is code
Hi first thank you for contest:) I have a little problem with problem C(Div2), I got Wrong answer in Test 11,but i dont know why?!!:( 13659056 Plz help me... Ty
Hey anybody there?!! Please help,im really confused
I'm wondering if anyone has solved Div1A by using a priority queue instead of counts? Such solution has O(n log n) asymptotics and hopefully should pass with n = 1000000 if using a fast implementation of PQ. Unfortunately it TLEd for me with stock java.util.PriorityQueue (13631725), probably because it treats those ints as objects instead of using an array of primitives.
I used priority queue but in C++..got correct answer
Can you help mr, please? I'm trying to solve Div2C/Div1A in Java. (http://ideone.com/SxR0n8) And got TimeOut at test11. How can I improve my solution?
I have a really simple idea for Div1A/Div2C Let there be Ci weights of weight = Wi.
Thus, total weights from Wi is Ci * (2^Wi) which is same as (Ci << Wi) — let's call this Ti
Let's bitwise OR all Ti forall i and call it T.
The number of set bits in T is the answer!
This is because if xth bit is set in T, we can safely make a group out of each ith weight class whose (x >> Wi) bit is set.
But, my solution times out :( — any idea why??
http://mirror.codeforces.com/contest/588/submission/13659655
Wi can be up to 10^6. If n=10^6 and all Wi=10^6, to OR all Ti will take 10^6*10^6=10^12.
ORing two numbers is not O(1), it's O(n) where n=number of digits. Check this (it's for addition): https://en.wikipedia.org/wiki/Computational_complexity_of_mathematical_operations
can anyone tell me why my solution for C div 1 gets TL ? http://mirror.codeforces.com/contest/587/submission/13660815
Can any one tell me way my approach is wrong for problem B/Div2
we now that each number n can be written as product of prime factors :
see the image
so i created prime sieve generator , and for each prime that divide n ( n%p == 0 ) , i add it once to the answer ( ans*=p )
what's wrong with this approach .
this is my submission 13667353
what if n is prime ?
in that case ans will be equal to 1 so i can print n but it's not the case for my submission .
If there is one prime larger than 10^7, like N = 2000000014 = 2 * 1000000007, then ans will be equal to 2, and you'll not add 10^9 + 7 to the answer.
you right , thanks
you're welcome =)
Could someone please outline the proof that the answer is the number of set bits in div1A/div2C? Thanks in advance!
In Div1: Problem A i understood number of set bits is equal to the unique number power of two addition But after that i didn't understand Why this algorithm working...
MAXN = 1000000 + log(1000000) bit[0..MAXN] = {} // all equal to zero ans = 0 for i = 1 to n bit[w[i]] ++ // of course after this, some bits maybe greater than 1, we'll fix them below for i = 0 to MAXN — 1 bit[i + 1] += bit[i]/2 // floor(bit[i]/2) bit[i] %= 2 // bit[i] = bit[i] modulo 2 ans += bit[i] // if bit[i] = 0, then answer doesn't change, otherwise it'll increase by 1
I think it is done this way Suppose we obtain this for two element array
[a, b]
a = bit[k] b = bit[k + 1]
Then,
a * 2^k + b * 2^(k + 1)
=> ((a/2)*2 + a0) * 2^k + b * 2^(K + 1)
=> a0 * 2^k + (a/2)*2*2^k + b * 2^(k + 1)
=> a0 * 2^k + (a/2)*2^(k + 1) + b * 2^(k + 1)
=> a0 * 2^k + ((a/2) + b) * 2^(k + 1)
So,
bit[k] = a0 = (a & 1)
bit[k + 1] = b + (a / 2)
Now, a0 = (a & 1), the least significant bit
A small correction for complexity of Div1B: it should be O(n k + n log n), not just O(n k), because of sorting. This can make a difference when n = 1000000 and k = 1.
Can anyone offer a brief explanation about problem E please? I really don't know what is the basis of a vector and why the answer is 2 ^ (b.size()) ...
Can someone explain the notation in Div-2 D/Div-1 B ?
Please correct if I am wrong, but I think that a valid subsequence of length x will contain exactly one element from the sequence [b[k*n], b[(k+1)*n-1] for every (k+1) <=x.
As far as I understand, dp[i][j] stores the number of subsequences of length j that pick element b[(j-1)*n+i] in the last round. If this were true, the final answer would be sum of all elements in dp[][] (minus cases where we counted the last element to be at an index greater than c). I don't understand the need for the quadruple summation and the multiplication with (c-j) at all.
Sorry. I posted at wrong section.
Can somebody explain Div. 1B/Div. 2D (Duff in Beach) ?
In Div1 B , How are we able able to satisfy condititon that : For each 1 ≤ j ≤ x - 1, (floor (i[j] / n)) + 1 = (floor (i[j + 1] / n)) ?? UPD : Got it.. :)
This is just an overcomplicated way to say that you should pick each member of your subsequence from a consecutive sequence of instances of the given sequence a. This formula looks so ugly that I have actually missed it during the contest:) This mistake made me count the number of any subsequences, not just consecutive ones. At least I have learned how to compute binomial coefficients for a fixed n up to 10^18 as a result of this failure :)
for Div 2C/ Div 1A .. could someone please explain how we actually counted Number of set bits in a sequence .. is that a particular algorithm for this question .. I am actually not bale to understand the working or logic behind the editorial given Plz HELP!!
Hello ankush, Really simple. When you have two set bits at pos i, this is equivalent to one set bit at pos (i+1). Hence the equation b[i] += b[i-1]/2. (since 2^(i-1) + 2^(i-1) = 2^i)
In DIV2E, In Haghani's code , why does he do nodey y = get(v,d[v]-d[p] + 1). Why is the +1 required? Wouldn't that be going further up than p?
The construction of the 2-SAT in Div1.D is really interesting! By the way, binary search is not necessary here. Just sort the edges by their destruction time in decreasing order, and set them to false in order until a contradiction occurs.
By problem Duff in the Army, I studied about LCA deeply. Thank you very much for this problem.
Isn't O(Q * sqrt(N) * log(N)) supposed to pass Div2E / Div 1C ? I used Mo's algorithm on trees according to this link .
Here is my submission:
With FAST I/O
WITHOUT FAST I/O
Div1 B, output doesn't match answer:
Author's code output: 30, but there are 48 non-decreasing subsequences, e.g.
What's wrong here?