helpme's blog

Need help in Hashing with overflow technique
By helpme, 9 years ago, In English

Hello everyone,

Recently I've read some tutorial on hashing, I learned that after some preprocessing we can find the hash of a substring in O(1) using modular inverse. But, I was surprised to see that people do not use modular arithmetic! For example, see this submission: 845264, How is it counting hash? Is it utilizing the integer overflow? Moreover, it does not use any modular inverse to find the hash of a substring, e.g.

inline int hh(int x,int y)
{
	return a[y]-a[x-1]*p[y-x+1];
}

I can't understand how it actually works. It would be great if any of you could explain this or suggest some online resources about this.

Thanks in advance!

  • Vote: I like it
  • -1
  • Vote: I do not like it

»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Yes, that code seems to be using integer overflow. However, this is generally not a good idea, as illustrated here: http://mirror.codeforces.com/blog/entry/4898

→ Reply
»
9 years ago, # |
  Vote: I like it +8 Vote: I do not like it

I'm going to answer your first question first.

Your suggestion is correct — it uses integer overflow. Basically, it's just counting hashes modulo 232 if we're talking about int. First problem with that was already pointed out: it's easy to construct a test which will fail all polynomial hashes modulo 2n. You're unlikely to get that "in real life", though, or even in some specific problems (say, if you're hashing a graph, I doubt authors will try to fail each and every way of hashing the graph).

Another problem is that integer overflow in signed types is undefined behaviour in C++. That is, if you calculate int a = 1e5, b = 1e6, c = a * b;, compiler is free to do anything it wants — if you're lucky, it will work just like integer overflow. In other cases (on other compilers, platforms and dates) program theoretically can wipe your HDD and install spyware (although I can't imagine any compiler really doing this). So, one should not rely on overflow in signed types. Unsigned are ok: int c = (unsigned int)a * (unsigned int)b is ok: we convert values to an unsigned type first, multiply them (and get expected overflow), then convert back by assigning to c. I would just typedef unsigned int hash; and calculate everything I need in the newly declared type.

→ Reply
»
9 years ago, # |
← Rev. 4   Vote: I like it +9 Vote: I do not like it

About modular inverse: you don't need it at all if you write polynomial hashes wisely, even if modulo is prime, etc.

I assume that you've seen the following pattern: if we have string a0a1... an - 1, then we consider a0 + a1p + a2p2 + ... + an - 1pn - 1 as its polynomial hash. Afterwards we can compute hashes for all prefixes of a given string (let's say hash of a0a1... ak is Sk) and if we ever need to calculate hash of alal + 1... ar, we take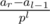 as an answer (division here is basically modular inverse).

However, there is another approach, which I like much more. We make rightmost characters in the string least significant, that is, hash of a0a1... an - 1 will now be a0pn - 1 + a1pn - 2 + ... + an - 2p + an - 1. Appending a character for string S is still easy, moreover, we don't need to know length of S: Hash(Sa) = Hash(S)·p + a.

Things get even better when we're talking about hashing substrings. If you have hashes for prefixes of lengths L and R, then answer is SR - SL - 1·pR - L. That is, we take hash for prefix of length R, then "cut out" leftmost (that is, most significant) characters (which we know to be first L of the initial string) and we have the answer immediately without modular inversion.

→ Reply
  • »
    »
    9 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    You really helped me a lot, Thank you! :)

    Btw, in this line: "if we ever need to calculate hash of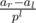 a_l a_l+1... a_r, we take " -- I think it would be (S_r - S_l-1)/P^l, isn't it?

    → Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Hi, could you explain the part

    Things get even better when we're talking about hashing substrings. If you have hashes for prefixes of lengths L and R, then answer is SR - SL·p^(R - L)]()

    in my imagination,if we want to hash the substring of aL, aL+1, aL+2, we can just take (SL+2 - SL)/p^L where SL is the prefix hash of length L, I dont understand why you multiply it by p^(R-L).

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
      ← Rev. 9   Vote: I like it +5 Vote: I do not like it

      Let's break it down. Assume that we have string a0a1a2a3a4a5 (that is n = 6). Then:

      • S0 = a0
      • S1 = a0p + a1
      • S2 = a0p2 + a1p + a2
      • S3 = a0p3 + a1p2 + a2p + a3
      • S4 = a0p4 + a1p3 + a2p2 + a3p + a4
      • S5 = a0p5 + a1p4 + a2p3 + a3p2 + a4p + a5

      We want to get hash of a2a3a4, that is, L = 2, R = 4. It should have form of a2p2 + a3p + a4. First, we take S4 as our initial approach:

      S4 = a0p4 + a1p3 + a2p2 + a3p + a4

      We see that it's almost what we need with several extra terms: a0p4 + a1p3. These terms are hash of substring a0a1000 (I've just took prefix of length five and replaced last three latters with zeros). That is, it's hash of a0a1 multiplied by p3, i.e. S1p3 = (a0p + a1)p3. So, if we subtract these two:

      • S4 - S1p3 = a0p4 + a1p3 + a2p2 + a3p + a4 - a0p4 - a1p3
      • S4 - S1p3 = a2p2 + a3p + a4

      We get exactly what we wanted.

      Does that make more sense now? Please note that there are other approaches with different formulas.

      → Reply